Теория надежности. Учебное пособие для студентов

• Название: Учебное пособие для студентов
• Анкор: Теория надежности.doc
• Дата: 07.05.2017
• Размер: 3.48 Mb.
• Имя файла: Теория надежности.doc
• Тип: Учебное пособие; #7212
• страница: 17 из 23

Математические методы прогнозирования

Методы прогнозирования надёжности ЭС разделяют на математические и физи­ческие. Математические методы прогнозирования, являющие­ся наиболее распространенными, подразделяют на детерминированные и вероятно­стные (стохастические), а также методы, основанные на применении математического аппарата теории распозна­вания образов. Детерминированный метод прогнозирования применяют при из­вестном характере изменения значений прогнозируемого параметра во времени. Тогда, представив состояние изделия в виде многомер­ной функции, можно описать его поведение в любой момент времени. Вероятностный метод прогнозирования предполагает определе­ние доверительного интервала значений прогнозируемого параметра в заданном временном интервале, в котором с заданной вероятно­стью параметр не выйдет за допустимые пределы изменения. Суть методов прогнозирования на основе распознавания образов состоит в следующем. В простран­стве имеется множество ярко выраженных областей, характеризую­щих состояние ЭС во времени. Зная значение параметра изделия в момент времени t₀, можно принять решение о принадлежности его к той или иной области, т.е. распознать образ исследуемого из­делия. Все эти методы позволяют прогнозировать состояние ЭС в будущем, контролируя его в настоящий период времени, на основе найденных экстраполяционных связей [20].

Методы прогнозирования на основе распознавания образов, подробно рассмотренные в [1], имеют несколько разновидностей: метод распознавания Байеса, метод последовательного анализа, метод минимального риска, метод наибольшего правдоподобия. Их изложение достаточно большое по объёму. Поэтому мы рассмотрим лишь два последних метода, описание которых заимствовано из [1].

Вначале рассмотрим метод минимального риска. Условимся характеризовать исправ­ное состояние РЭС диагнозом D₁, неисправное состояние - диаг­нозом D₂. При распознавании состояния РЭС при постановке ди­агноза могут быть допущены два рода ошибок. Ошибками пер­вого рода называют такие, когда ставится диагноз D₂ вместо D₁, т.е. исправную РЭС относят к неисправной. Эти ошибки часто называют ложной тревогой или риском поставщика. Ошибками второго рода называют такие, когда для неисправ­ной РЭС с состоянием D₂ ставят диагноз D₁, т. е. считают ее годной. Эти ошибки называют пропуском цели или риском заказчика. Естественно, что такого рода ошибки являются более опасными. Поэтому ошибки первого и второго рода имеют раз­личные цены (веса). Будем полагать, что процесс распознавания состояния РЭС осуществ­ляется при наличии одного диагностического признака, проводить дифференциальную диагностику и считать, что априорные вероят­ности диагнозов P(D₁) и P(D₂) известны из предварительных (собранных до прогноза) статистических данных.

В методе минимального риска решающее правило при­нятия решения выбирается исходя из условия минимума риска. Обозначим диагностируемый параметр через х. Тогда задачу распознавания можно сформулировать так: необходимо выбрать граничное (оптимальное) значение параметра х, равное х₀, такое, чтобы при х < х₀ диагностируемая РЭС находилась в исправном состоянии, а при х > х₀ выходила из строя и снималась с даль­нейшей эксплуатации. Очевидно, что решающее правило для пос­тановки диагноза будет при этом следующим:

при х < х₀ x  D₁ , при х > х₀ x  D₂. (6.22)

Обозначим возможные решения, которые в принципе могут быть приняты в соответствии с решающим правилом (6.22), че­рез Η_ij (i, j = 1, 2). Будем при этом считать, что i означает по­ставленный диагноз, а j - действительное состояние системы. Правильными решениями будут Н₁₁ и Н₂₂ (т.е. когда поставленный диагноз совпадает с действительным). Решение Н₁₂ означает пропуск цели, а Н₂₁ - ложную тревогу.

Вычислим вероятности принятия неправильных решений Р(Н₁₂) и Ρ(Н₂₁). Очевидно, что они будут равными произведению вероятностей двух событий: наличия неисправного состояния и значения х < х₀ и наличия исправного состояния и значения х > х₀ соответственно:

(6.23)

(6.24)

где P₁ = P(D₁) и P₂ = P(D₂) - вероятности априор­ных диагнозов; Р(х < х₀ / D₂) и Р(х > х₀ / D₁) - вероятности исправно­го и неисправного состояний в соответствии с решающим прави­лом (6.22). Будем считать, что цена (вес) принятия неправильного реше­ния Р(Н₁₂) - пропуска цели - равна С₁₂, а цена решения Ρ(Н₂₁) - ложной тревоги - С₂₁. Тогда средний риск принятия решения R будет равен сумме вероятностей возможных ошибок с учетом их весов, т.е.

R = С₁₂  Р(Н₁₂) + С₂₁  Ρ(Н₂₁) (6.25)

(обычно С₁₂ >> С₂₁). Обозначим цены правильных решений Н₁₁ и Н₂₂ через С₁₁ и С₂₂ соответственно. Чтобы отличить от стоимости потерь, их обычно считают отрицательными. С учетом сказанного выражение среднего риска может быть уточнено: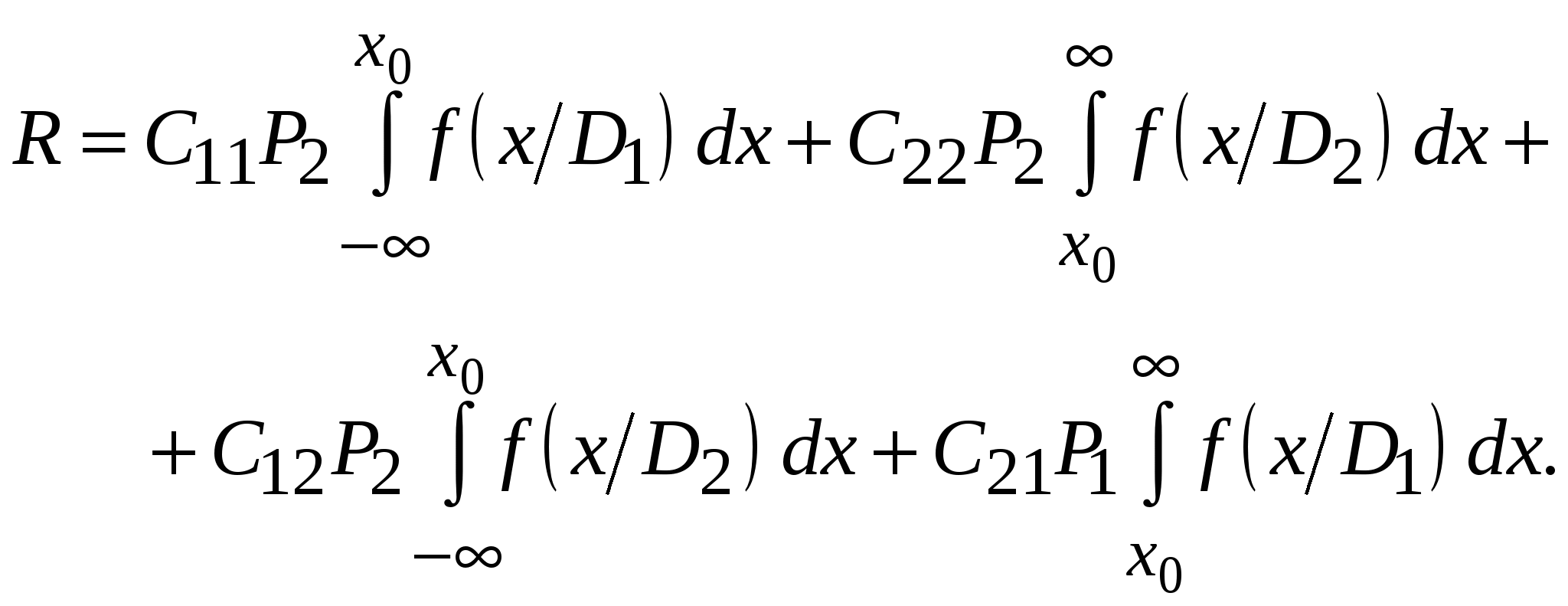

(6.26)

Иногда цены правильных решений С₁₁ и С₂₂ полагают равными нулю, т.е. не учитывают как, например, в (6.25). Рассмотрим математическое содержание метода минимального риска. Из условия получения минимума среднего риска R_min определим граничное значение х₀ диагностируемого параметра х в решающем правиле (6.22). Необходимое и достаточное условие достижения R_min в точке х = х₀ выражается неравенством

(6.27)

Для получения выражения (6.27) в явном виде определим сна­чала условие существования экстремума функции (6.26), т.е. решим уравнение вида

(6.28)

С учетом (6.26) оно запишется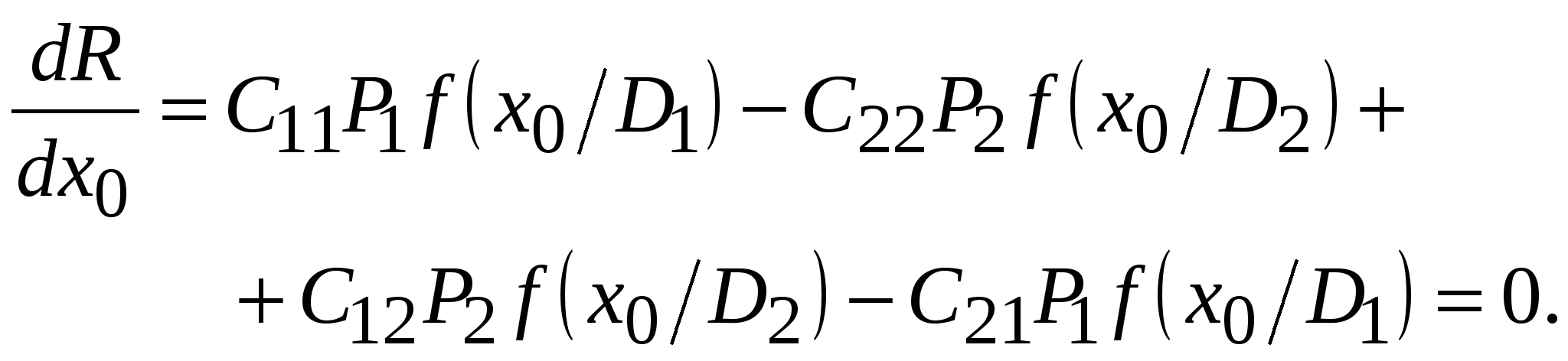

(6.29)

или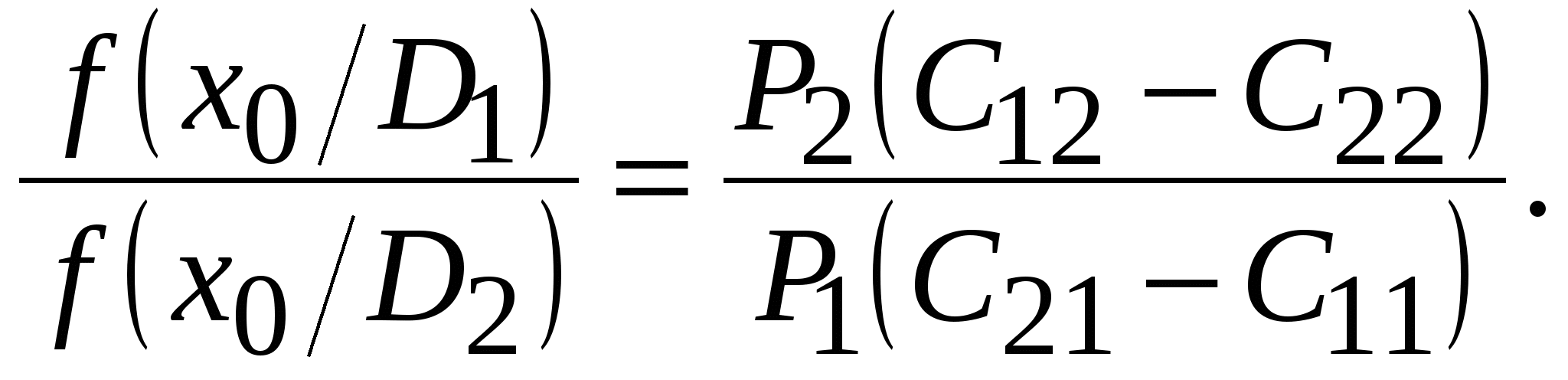

(6.30)

Пусть плотности распределения f(х / D₁) и f(х / D₂) подчинены нормальному закону и имеют по одному максимуму (рисунок 6.5). Искомое оптимальное значение х₀, доставляющее минимум функ­ции риска R, будет располагаться на рисунке 6.5 между центрами х₁ и х₂ распределений f(х / D₁) и f(х / D₂), т.е.

х_1СР < х₀ < х_2СР. (6.31)

С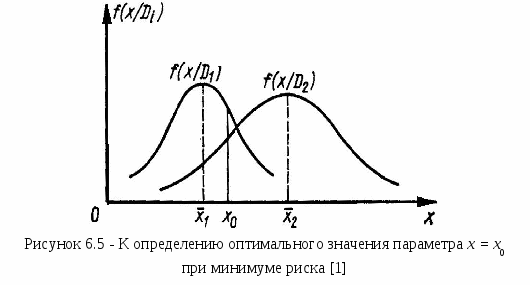
учетом положения x₀ теперь можно утверждать, что условие (6.27) приводит к необходимости выполнения следующего неравенства относительно производных плотностей распределения: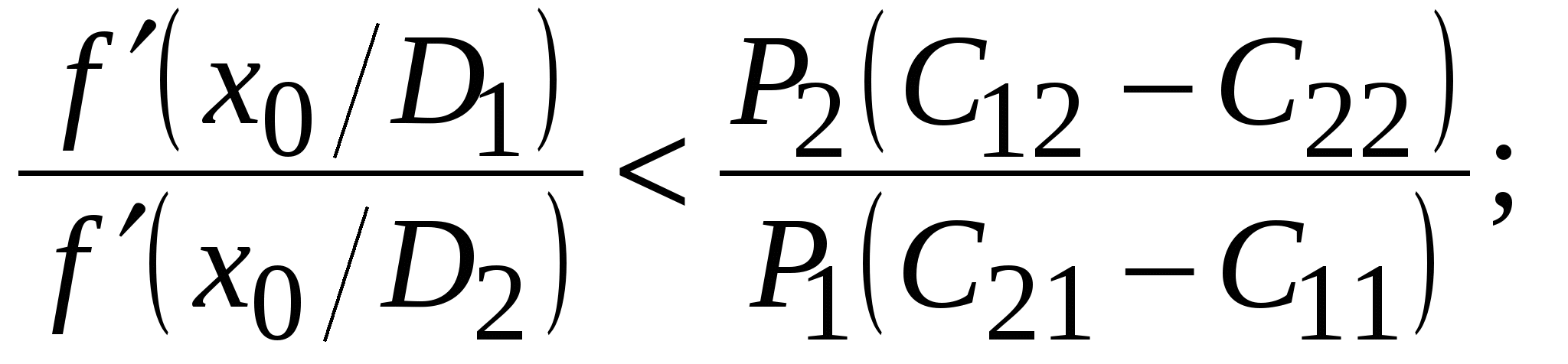

(6.32)

Заметим, что (6.32) всегда выполняется, так как в правой час­ти неравенства стоит положительная величина, а слева отрица­тельная. Это объясняется тем, что С₁₂ > С₂₂, a С₂₁ > С₁₁ и при х > х₁ производная f'(х₀/D₁) < 0, а производная f '(х₀/ D₂) > 0 вплоть до х₀ < х_2СР (см. рисунок 6.5).

Запишем решающее правило метода минимального риска с использованием отношения правдоподобия (6.30) и условия (6.22):

x  D₁, если f(х/D₁) / f(х/D₂) > P₂(С₁₂ - С₂₂) / [P₁(С₂₁ - С₁₁)]; х < х₀; (6.33)

x  D₂, если f(х/D₁) / f(х/D₂) < P₂(С₁₂ - С₂₂) / [P₁(С₂₁ - С₁₁)]; х > х₀; (6.34)

Пороговым значением отношения правдоподобия счи­тают величину

λ = P₂(С₁₂ - С₂₂) / [P₁(С₂₁ - С₁₁)]. (6.35)

Если цены принятия правильных решений С₁₁ и С₂₂ не учитывают, т.е. считают их равными нулю, то выражение (6.35) принимает вид

λ = P₂С₁₂ / (P₁С₂₁). (6.36)

Используем метод минимального риска при решении диагностической за­дачи.

Пример 6.7 [1].

В преобразователе частоты при нормальной работе в состоянии D₁ среднее значение частоты F_СР = 400 Гц, а ее среднеквадратическое отклонение σ = 15 Гц. При неисправном D₂ состоянии пре­образователя F₂ = 430 Гц, а σ₂ = 50 Гц. Из статистических данных известно также, что у 5% таких преобразователей при эксплуатации наблюдаются отказы. Требуется определить предельную частоту F₀ преобразователя, при которой еще можно продолжать его эксплуатацию, имея в виду, что отношение стоимости пропуска цели С₁₂ к стоимости ложной тревоги C₂₁ равно 50.

Решение.

Будем считать, что распределение частоты у исправного и неисправного преобразователей подчиняется нормальному закону, а С₁₁ = С₂₂ = 0. Тогда из условия (6.30) получим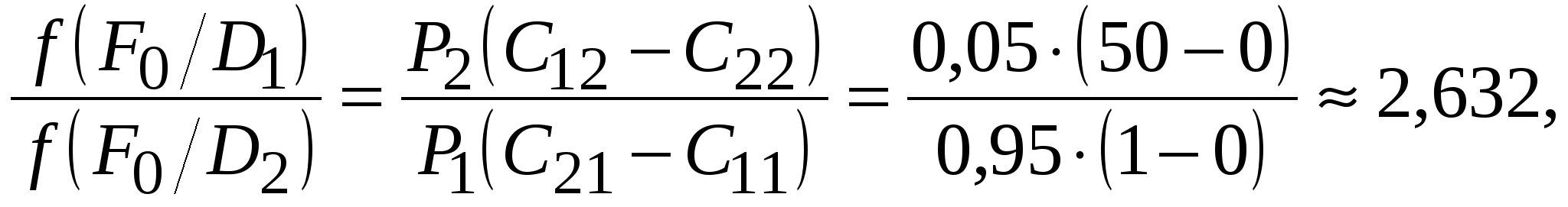



где Р₂ = 0,05 и P₁ = 1- Р₂ = 0,95 - вероятности пребывания преобразователя частоты соответственно в неисправном и исправном состояниях. Плотности распределения при нормальном законе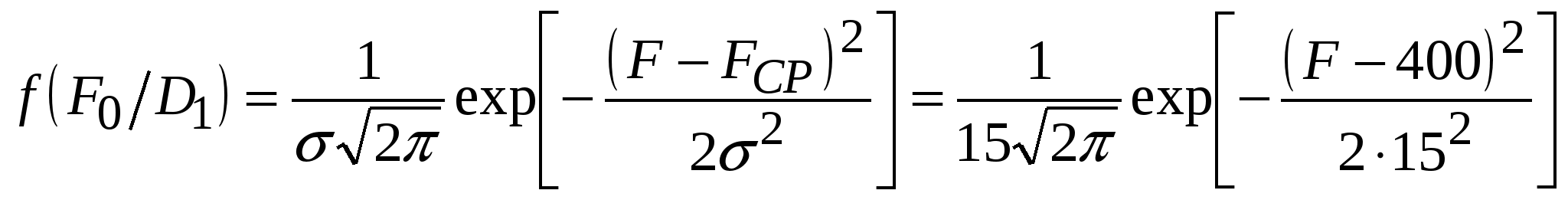

;



Подставим полученные значения в предыдущее равенство и, логарифмируя его, получим

-(F - 400)² / (215²) + (F - 430)² / (250²) = ln(2,632 15 / 50) = - 0,2362.

Это уравнение можно упростить:

F² - 0,79410³F + 15,7410⁴ = 0.

Положительный корень этого уравне­ния F₀ = 411,46. Следовательно, мож­но рассчитывать на то, что до часто­ты 411,46 Гц преобразователь будет работать нормально. Очевидно, что отклонение частоты преобразователя от его среднего значения не должно превышать 411,46 – 400 = 11,46 Гц при его нормальной работе. Полученное решение может быть проиллюстрировано графиче­ски на рисунке 6.3, если принять х₁ = 400 Гц, х₂ = 430 Гц, а х₀ = 411,46 Гц.

Метод наибольшего правдоподобия, как и метод минимального рис­ка, для записи своего решающего правила использует отношение правдоподобия

x  D₁, если f(х/D₁) / f(х/D₂) > 1; (6.37)

x  D₂ ,если f(х/D1) / f(х/D₂) < 1, (6.38)

где x - диагностируемый параметр.

Граничное значение х = х₀ находят из следую­щего условия:

f(х/D₁) = f(х/D₂). (6.39)

Сравнивая (6.39), (6.35) и (6.30), видим, что они совпадают, если

λ = P₂(С₁₂ - С₂₂) / [P₁(С₂₁ - С₁₁)] = 1. (6.40)

Из этого следует, что метод наибольшего правдоподо­бия является частным случаем метода минимального риска. При С₁₁ = С₂₂ = 0 (6.40) приобретает вид

P₂С₁₂ / (P₁С₂₁) = 1. (6.41)

Отметим в заключение, что всегда надо иметь в виду, что P₁ >> Ρ₂ и С₁₂ >> С₂₁. Метод наибольшего правдоподобия проиллюстрируем примером 6.8.

Пример 6.8 [1].

Условия задачи совпадают с примером 6.7. Необходимо решить ее методом наибольшего правдоподобия.

Решение.

Значение граничной частоты F₀ преобразователя определим из ус­ловия (6.39). Используя данные примера 6.7, получим



После логарифмирования это равенство приводится к виду:

F² - 0,79410³F + 15,7510⁴ = 0.

Положительный корень полученного уравнения F₀ = 407,44. Следовательно, граничное значение частоты F₀, при котором будут еще сохране­ны нормальные условия функционирования преобразователя, будет F₀ = 407,44 Гц. Сравнивая результаты решений в примерах 6.7 и 6.8, убеждаемся в их близости. Незначительные их расхождения обусловлены приближенностью ис­пользованных методов прогнозирования.

Точность предсказа­ний, которую они гарантируют, примерно одного порядка, но для их использования требуется различный объем статистической ин­формации. Наибольший он в методе Байеса, наименьший - в ме­тоде последовательного анализа. В инженерной практике все же несколько боль­шее распространение получили методы последовательного анали­за и минимального риска.

Физические методы прогнозирования

Физические методы прогнозирования надёжности РЭС базируются на анализе физических и физико-химических процессов, протекающих в РЭС под влиянием дестабилизирующих факторов. Наиболее подробно эти методы описаны в [20], откуда и взят материал данного подраздела.

Так как износ и разрушение реальных устройств обычно локализованы и зависят от конкретных причин, то наиболее приемлемой моделью надёжности ЭС является физическая модель, основанная на принципе суммирования компонентов надёжности, каж­дый из которых представляет надёжность элемента фи­зической структуры (ЭФС) изделия. Под физическими моделями надёжности понимают математическое описа­ние физических процессов и явлений, определяющих параметры надёжности изделий. Любое изделие в них делят на ЭФС, каждый из ко­торых имеет свою характеристику надёжности.

Изучение и моделирование кинетики процессов, про­исходящих в выделенных ЭФС, позволяет установить связь между их геометрией, свойствами материалов, экс­плуатационными факторами и временем наработки ЭС до отказа. При этом следует учитывать, что в каждом ЭФС может действовать несколько механизмов отказа. Следовательно, каждый компонент надёжности необхо­димо рассматривать как систему, число элементов в которой равно числу действующих механизмов отказов.

При прогнозировании надёжности результаты фи­зических исследований должны дополняться данными анализа отказов и данными статистического характера. Их можно получить при работе ЭС в форсированных рабочих ре­жимах при испытании, что лежит в основе метода уско­ренных испытаний. Ускорить физико-химические процессы, приводящие к отказу, можно усиливая нагрузку на ЭС при испытании (температуру, напряжение, ток, дав­ление, скорость вибрации, частоту циклов и т.д.), т.е. в форсированном режиме. Ускоренными форсированными называют испытания в форсированных режимах с последующей экстраполяцией полученных результатов к условиям испытаний ЭС в нормальных режимах.

Физическая сущность ускоренных испытаний заключается в ус­корении только того механизма отказов, который является харак­терным для испытываемых изделий при их работе в нормальном режиме. Поэтому при увеличении нагрузки на ЭС с целью сокраще­ния времени испытания на надёжность необходимо всегда иметь в виду, что механизм отказов должен сохраняться неизменным. Это является наиболее сложной проблемой ускоренных испытаний, по­скольку выявить характерный механизм отказов бывает иногда очень трудно.

Опыт показывает, что механизм отказов при испытании изделий в форсированном режиме остается тем же самым, что и при испы­тании в нормальном режиме, если закон распределения вероятно­сти безотказной работы и коэффициент вариации остаются неизмен­ными при переходе от нормального режима к форсированному. В этом случае графики зависимости вероятности безотказной работы Р(t) от отношения t / M(t) для форсированного и нормального ре­жимов испытаний совпадают и можно графически экстраполировать результаты ускоренных испытаний к нормальным условиям.

Выбор величины нагрузки, прикладываемой для ускорения ис­пытаний изделий, определяется не только требованием сохранения механизмов отказов, характерных для нормального режима, но и прочностными характеристиками испытываемых изделий. Наиболее изученными в настоящее время являются физико-стати­стические модели старения изделий, созданные в результате недорогих ускорен­ных испытаний, проводимых при термической нагрузке. Установлено, что протекающие во многих материалах физико-химические процессы, обусловливающие старе­ние ЭС под действием термической нагрузки, достаточно точно описываются уравнением Аррениуса. Уравнение Аррениуса характеризует зависимость скорости химической реакции от абсолютной температуры Т при постоянном объеме и имеет вид:

(6.42)

где J – количество вещества, вступающего в реакцию; dJ / dt – скорость реакции; С - константа; q - заряд электрона; Е - энергия активации, необходимая для вступления молекул в химическую реакцию; k - постоянная Больцмана. Чем больше Е, тем меньше скорость химической реакции. После преобразований уравнение (6.42) при­нимает вид

lg t_ср= C₁Е / Т + lg C₂ , (6.43)

где С₁ = q / (2,303k); С₂ = const; t_ср - статистическая оценка средней наработки на отказ.

Если построить зависимость (6.43) в координатах lg tср и 1/Т, по­лучим семейство прямых (рисунок 6.6, а), каждой из которых соответст­вует постоянное значение отказов. Отрезок, отсекаемый прямой 1 или 2 на оси ординат, равен lg C₂, а тангенс угла φ наклона этой прямой связан с энергией активации соотношением tg φ = C₁Е. Чем больше энергия активации, тем больше угол φ и тем выше надёжность изделий. Рассмотрим прямые 1 и 2 на рисунке 6.6, а, характеризующие соответственно результаты испытания изделий двух типов при термической нагрузке. При одном и том же приращении нагрузки (1 / Т₂ - 1/ Т₁) для отказа одного и того же процента из­делий второго типа потребуется меньше времени, чем для изделий первого типа. Следовательно, изделия первого типа более надежны. Таким образом, по углу наклона прямой или по значению энергии активации можно сопоставить качественно (по принципу «лучше - хуже») надёжность двух (и более) типов изделий. Если сравнить различные модификации одного и того же изделия, то изменение угла наклона прямой характеризует лишь изменение конструкции изделия (улучшение или ухудшение), в то время как параллельное перемещение этой прямой характеризует технологические изменения. Прямая является графическим изображением зависимости (6.43) только в том случае, если механизм отказов во всем рассматриваемом диапазоне нагрузок остается неизменным. Если же механизм отказов при увеличении или уменьшении нагруз­ки изменяется, то, как правило, изменяется и энергия активации, что приводит к появлению изломов на прямой.

Н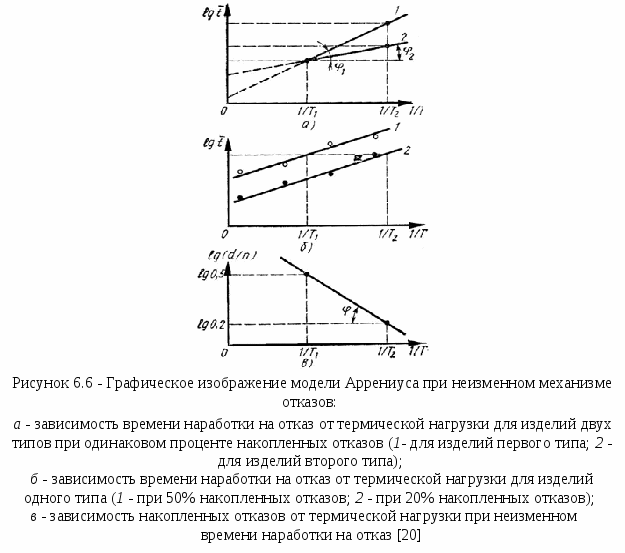
а практике обычно добиваются линейной зависимости лога­рифма отношения числа d отказов в выборке к ее объему n от ве­личины нагрузки. В этом случае старение изделий может быть опи­сано также моделью Аррениуса, но вид зависимости (6.43) несколь­ко изменится. Поскольку энергия активации пропорциональна величине С tg φ, в (6.43) нельзя автоматически заменить время зна­чением накопленных отказов (%). Однако графическим путем не­трудно перейти к зависимости накопленных отказов (%) от нагруз­ки. Для этого предположим, что испытания при различных терми­ческих нагрузках проходят восемь равных выборок, взятых из од­ной и той же партии изделий, и механизм отказов всех изделий в этом эксперименте один и тот же. В процессе испытаний зафикси­руем время, в течение которого в первых четырех выборках отка­жет, например, 20% изделий, а во вторых четырех - 50%. Учиты­вая, что на каждую группу выборок подавалось четыре различных значения нагрузки, получим восемь различных значений времени на­работки на отказ. Выделив их на графике зависимости lg t_ср от 1 / Т и соединив точки при одном и том же проценте накопленных отка­зов, построим две прямые параллельные линии (рисунок 6.6, б). Восста­вим перпендикуляр из любой точки оси ординат до пересечения с прямыми 1 и 2. Проекции точек пересечения на ось абсцисс дадут значения 1 / Т₁, и 1 / Т₂ соответствующие двум значениям логарифма накопленного процента отказов. Нанеся эти значения на график за­висимости lg (d / n) от 1 / Т и соединив полученные точки, построим прямую (рисунок 6.6, в), которая описывается уравнением Аррениуса. Эта прямая определяет значения накопленных отказов (%) в зави­симости от нагрузки за определенный промежуток времени, а по углу ее наклона можно судить о факторе ускорения.

При постоянном механизме отказов по результатам испы­тания изделия в форсированном режиме в течение вре­мени t_у можно судить о времени испытания изделий t = K_yct_у в нормальном режиме для получения того же числа отказов. По моде­ли Аррениуса фактор ускорения равен

K_yc = ехр[-(qЕ / k)  (1 / Т₂ – 1 / Т₁)], (6.44)

где Т₁ и Т₂ - температура при форсированном и нормаль­ном режиме соответственно (Т₁ > Т₂). Для более надежных изделий фактор ускорения меньше, чем для менее надежных [20].

6.6.1 Определительные ускоренные испытания на надёжность с использованием прогнозирования

Ускоренные испытания служат для получения в укороченный промежуток времени t_у до появле­ния в РЭС первого отказа необходимой диагностической информа­ции, по которой можно судить о состоянии РЭС при ее дальней­шей технической эксплуатации в течение времени t при t_y << t.

Введение между работоспособным и неработоспособным состояниями промежуточного предотказового состояния характеризует процесс накопления нарушений в контролируемом объекте или, что то же самое, процесс изменения технического состояния, предшествующий возникновению неработоспособного состояния контролируемого объекта. Предотказовым состоянием изделия называется такое его состояние, при котором накапливающиеся в нем нарушения, различимые с помощью заданных средств и мето­дов, не препятствуют в течение некоторого периода времени безотказной работе.

Различают ускоренные испытания в нормальном и форсиро­ванном режимах. Ускорение испытаний в нор­мальных условиях можно достигнуть назначением более жестких допусков Δх_И на изменение диагностируемого параметра х по сравнению с допуском на него Δх, заданного ТУ. Время t_y, в течение которого х не выйдет за границы Δх_И, будет меньше времени t его пребывания в границах допуска Δх. Другим способом ускорения испытаний в нормальных услови­ях является увеличение объема испытуемой партии, так как с увеличением числа проверяемых приборов увеличивается вероят­ность появления отказов [1].

Существует также ряд эмпирически установленных косвенных признаков, по изменению которых можно с определенной досто­верностью судить о предотказовом состоянии объекта и, следовательно, прогнозировать в скором будущем наступление отказа. Определение предотказового состояния по этим признакам осуществляют методами локальной и методами интегральной диагностики. Методы интегральной диагностики позволяют обнаружить потенциально ненадёжные изделия, например, изделия со скрытыми дефектами, нестабильными характеристиками и др. Но они не позволяют установить причину дефекта или локализовать его местоположение в изделии.

К методам локальной диагностики относятся: методы дефектоскопии (рентгеновские, тепловые, ультразвуковые и др.), методы физического эксперимента (растровая электронная микроскопия, радиоспектральные методы и др.) и методы локального измерения специально выбранных характеристик электромагнитных, тепловых и других полей.

При предотказовом состоянии происходит измене­ние спектра электрического шума полупроводниковых приборов и увеличение средней мощности такого шума, увеличение перегрева радиоэлементов, появление характерных для предотказового состояния звуков при работе электродвигателей, вентиляторов подшипников и т.п. При подаче синусоидального напряжения на участок цепи, имеющий строго постоянное (не зависящее от силы тока, протекающему по нему) сопротивление, ток, протекающий через элемент будет тоже строго синусоидальным. Несинусоидальность тока при подаче на участок цепи строго синусоидального напряжения свидетельствует о том, что в цепи имеется переменное, зависящее от тока сопротивление. Если элементы в цепи должны иметь строго постоянное сопротивление, значит, в цепи возник ненадёжный контакт, представляющий собой источник нелинейности. Степень искажения оценивают по доле третьей гармоники в кривой тока. Прогнозирование надёжности полупроводниковых приборов производят по отклонению формы вольтамперной характеристики от образцовой. Более подробно вопросы диагностики предотказового состояния при неразрушающем контроле элементов и узлов радиоэлектронной аппаратуры изложены в [29].

Ускоренными испытаниями в форсированных режимах (или просто форсированными испытаниями) называют такие, которые проводят в условиях форсирования процесса возникновения отка­зов. Создать такие условия можно, изменив, например, тем­пературу, влажность и давление среды, в которой осуществляется испытание, или увеличив рабочие нагрузки и диапазон частот, в котором работает прибор. Форсированные режимы ускоряют фи­зико-химические процессы в материалах испытуемых изделий и способствуют более быстрому развитию в них процессов износа и старения.

В качестве примера приведём результаты ускоренных испытаний на срок службы в форсированном циклическом режиме транзисторов типа П210 (рисунок 6.7). Испытания проводились в 50 нагрузочных циклов одинаковой д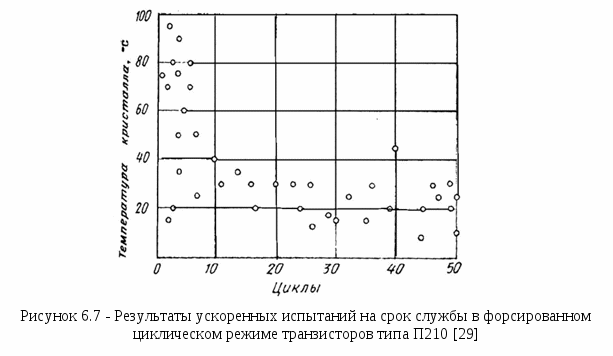
лительности и напряжённости.

Транзисторы, имеющие большое тепловое сопротивление переход- корпус и соответственно повышенные температуры кристалла, имеют значительно меньший срок службы, чем остальные транзисторы. Транзисторы, имеющие тепловое сопротивление ниже определённого уровня, имеют срок службы, практически не зависящий от теплового сопротивления. Надёжность этих транзисторов определяется другими факторами, а у транзисторов с большим тепловым сопротивлением, тепловое сопротивление является доминирующим фактором, определяющим их надёжность.

Для обнаружения предотказовых состояний с целью прогнозирования надёжности различных элементов можно использовать переходные тепловые характеристики. Результаты прогнозирования надёжности резисторов по переходным тепловым характеристикам иллюстрируются рисунком 6.8, на котором приведены графики изменения сопротивления резисторов типа МЛТ-0,5 во времени форсированных испытаний при импульсной нагрузке с повышенным тепловыделением. Амплитуда и длительность импульса выбираются такими, чтобы выделяемая в резистивном элементе энергия была немного меньше энергии, приводящей к необратимым изменениям в резисторе. В результате исследований, проводившихся на резисторах типа МЛТ мощностью 0,5 Вт было установлено, что для резисторов, не имеющих дефектов, изменение сопротивления (рисунок 6.8, а) имеет линейный характер при длительности импульса не более 5 с и мощности не превышающей номинальную более чем в 4-7 раз.

Т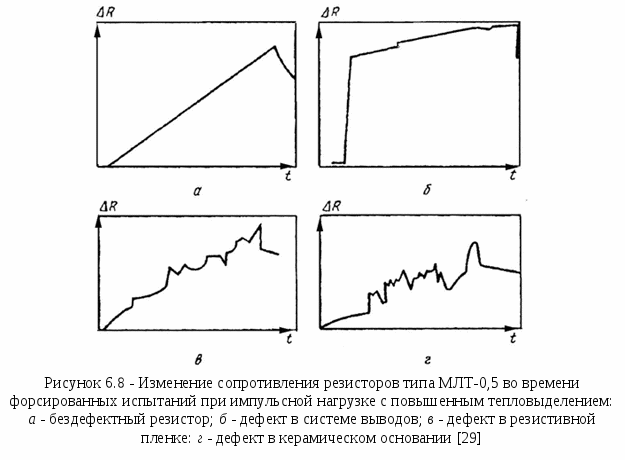
емпературная зависимость изменения сопротивления резистора с различными дефектами изображена на рисунке 6.8 б, в, г. Было подвергнуто исследованию 1180 резисторов, значительная часть которых специально была выбрана из числа забракованных производственным контролем. У 136 резисторов была обнаружена нелинейная характеристика. Вся партия была подвергнута испытаниям при номинальной нагрузке в течение 5000 ч при повышенной температуре. За это время отказало 13 резисторов, 11 из них имели нелинейную характеристику (8,1 % от общего количества таких резисторов) и 2-линейную (0,19% от общего количества резисторов с линейной характеристикой). При данном режиме испытаний резисторы с нелинейной характеристикой отказывали почти в 50 раз чаще, чем резисторы с линейной характеристикой. Поэтому появление у резистора во время эксплуатации нелинейности в переходной тепловой характеристике можно считать прогнозом появления в ближайшем времени его отказа.

В основе идеи ускоренных испытаний при форсированных ре­жимах лежат уравнения вида [1]

q₀(ε₀, t₀ ) = φ[q_Ф(ε_Ф, t_y)], (6.45)

λ₀  t₀ ≈ λ_Ф  t_y, (6.46)

где q₀, q_Ф - соответственно вероятности возникновения отказов в нормальном и форсированном режимах; ε₀, ε_Ф - признаки, харак­теризующие соответственно нормальное состояние РЭС и ее со­стояние при форсированных испытаниях; t₀, t_y - время работы РЭС, гарантированное ТУ для работы в нормальном режиме, и время форсированных испытаний; λ₀ и λ_Ф - интенсивности отказов РЭС при работе в нормальном и форсированном режимах.

Проиллюстрируем графически возможность практического ис­пользования уравнений (6.45) и (6.46). Для этого по известным статистическим данным построим график q₀(ε₀, t₀) = f(t). Пусть он, например, имеет вид кривой во втором квадранте на рисунке 6.9. Форсированные испытания проведем в интервале времени t_y. Полученный в результате график q_Ф(ε_Ф, t_{y) =} φ(t) поместим в первый квадрант рисунка 6.9. Зная время t_y (как показано на рисунке стрелками), определим q = q_Ф и приравняем ее к q₀, т.е. q_Ф = q₀. По из­вестному q₀ и кривой q₀(ε₀, t₀) = f(t) определим искомое t₀.

О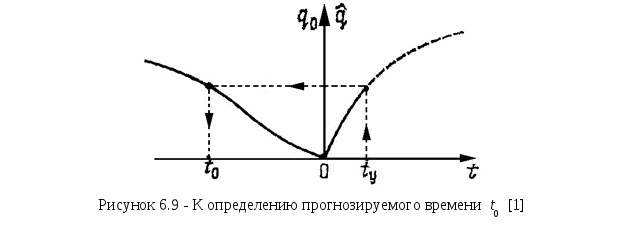
тно­шение t₀ / t_y = λ_Ф / λ₀ [в соответствии с (6.46)] называют коэффициен­том ускорения испытаний.

Форсированные испытания менее точны, чем ускоренные в нормальном режиме, а последние усту­пают испытаниям, проводимым в нормальных условиях и в нату­ральном масштабе времени [1].

Для экстраполяции результатов ускоренных испытаний в нормальном режиме необхо­димо знать истинное распределение наработки на отказ испытывае­мых изделий. Подходить к этой проблеме нужно так же, как к ре­шению любой статистической задачи, не делая заранее предположе­ний о законе распределения. Для установления закона распределения следует обязательно удалить из генеральной совокупности изделия с ранними отказами (потенциально ненадежные), так как появление ранних отказов из-за дефектов изготовления может привести к по­лучению распределения, отличающегося от истинного. При этом не­обходимо выбрать такое время испытания, которое позволит не только удалить из исследуемой совокупности потенциально ненадеж­ные изделия со скрытыми дефектами, но и установить истинное рас­пределение наработки на отказ. Тогда, например, при экспоненциальном законе распределения вероят­ности безотказной работы значения вероятностей Р₂(t_Г) и Р₂(t_И), заданных на гарантированное время безотказной работы t_Г и на время ускоренных испытаний в нормальном режиме t_И, связаны соотношением (6.7), приведённым ранее в разделе 6.1.2:

ln Р₂(t_И) = [ln Р₂(t_Г)]  t_И / t_Г. (6.7)

Испытания ЭС для определения фактора ускорения можно осуществлять при фиксированной или переменной нагрузке. Из испытаний при переменной нагрузке большой практический интерес представляют испытания РЭС методом шаговой нагрузки (ступенчатые испытания). При этом методе первоначально измеряют значения вы­бранных параметров-критериев годности (ПКГ) изделий, после чего изделия подвергают действию нагрузки. По окончании испытания снова изме­ряют параметры РЭС с целью обнаружения отказов. За­тем эти же РЭС вновь подвергают воздействию большей нагрузки. Шаговое (ступенчатое) увеличение нагрузки производят до тех пор, пока не будет достигнут опреде­ленный процент отказов. Преимущество метода ступенчатых испытаний по сравнению с методом испытаний при фиксированной на­грузке состоит в том, что требуется меньшее число изде­лий для определения фактора ускорения и режима уско­ренных испытаний, так как достаточно лишь одной вы­борки, чтобы выявить ту перегрузку, при которой сохраняется один и тот же механизм отказов. Кроме то­го, при ступенчатом методе испытаний затрачивается меньшее время для получения информации о надёжности испытываемых изделий, так как отказы наступают за меньший промежуток времени, чем при фиксированной нагрузке, за счет эффекта накопления деградационных изменений в физической структуре объекта испытаний по мере перехода от одной ступени к другой. Благодаря от­меченным преимуществам метод ступенчатых ускоренных испытаний может быть полезен на раннем этапе исследо­вания надёжности изделий. Однако в процессе разработ­ки этого метода приходится сталкиваться с рядом труд­ностей, которые отсутствуют при испытании при фикси­рованной нагрузке. Это выбор высоты ступени (приращение нагрузки) и продолжительности этой сту­пени (времени действия на изделие данной нагрузки) [20].

Например, при уменьшении продолжительности сту­пени возрастает интенсивность отказов по сравнению с испытаниями при фикси­рованной нагрузке. Это связано с тем, что один уровень нагрузки может влиять на результаты последующих более высоких нагрузок, что затрудняет интерпретацию результатов испытаний.

Итак, ускоренные испытания позволяют:

• 
  прогнозировать интенсивность отказов при данной нагрузке или при данных условиях путём экстраполяции за пределы периода испытания изделия при этих условиях;
  
• 
  установить корреляцию между сроком службы изделия и уровнями нагрузок с целью предсказания путём экстраполяции отказов изделий на других уровнях нагрузок;
  
• 
  выявить влияние различных факторов на надёжность изделия;
  
• 
  разработать методы испытаний изделий на надёжность, обеспечивающих получение максимума сведений при минимальных затратах.
  

Ускоренные испытания могут быть использованы для количественной оценки надёжности только тогда, когда фактор ускорения, полученный путём сравнения результатов испытания под нормальной и форсированной нагрузками остаётся в процессе производства или в процессе эксплуатации изделий неизменным. Если учесть также, что всякого рода экстраполяции обладают сравнительно низкой точностью, то результаты ускоренных испытаний могут служить только для ориентировочной оценки показателей надёжности.