Теория надежности. Учебное пособие для студентов

• Название: Учебное пособие для студентов
• Анкор: Теория надежности.doc
• Дата: 07.05.2017
• Размер: 3.48 Mb.
• Имя файла: Теория надежности.doc
• Тип: Учебное пособие; #7212
• страница: 4 из 23

3.Показатели надёжности

3.1.Общие сведения о показателях надёжности для различных видов объектов

Надёжность относится к числу свойств, которые проявляются при ис­пользовании изделий по назначению в тече­ние некоторого времени. Количе­ственная характеристика одного или не­скольких свойств, составляющих на­дёжность объекта называется показателем надёжности. Наборы показателей, описывающих надёжность объекта, отличаются, в зависимости от того, яв­ляется ли объект обслуживаемым, восстанавливаемым, ремонтируемым или нет.

Техническое обслуживание - это комплекс работ (операций) для под­держания РЭС в исправном или работоспособном состоянии при подготовке и применении по назначению, хранении и транспортировании [50].

Восстановление - это процесс перевода объекта в работоспособное состояние из неработоспособного состояния.

Ремонт - это комплекс операций по восстановлению исправности или работоспособности и восстановлению ресурсов РЭА или её составных частей [4].

Обслуживаемый объект - это объект, для которого проведение техни­ческого обслуживания предусмотрено нормативно-техни­ческой документа­цией и (или) конструкторской (проектной) документацией, а необслуживае­мый объект- это объект, для которого проведение технического обслужива­ния не предусмотрено этой документацией.

Восстанавливаемый объект - это объект, для которого в рассматриваемой си­туации проведение восстановления работоспособ­ного состояния предусмотрено в нормативно-тех­нической и (или) конструкторской (проектной) документации, а невосстанавливаемый объект- это объект, для которого в рассматриваемой си­туации проведение восстановления работоспособ­ного состояния не предусмотрено этой документацией.

Ремонтируемый объект - это объект, ремонт которого возможен и преду­смотрен нормативно-технической, ремонтной и (или) конструкторской (проектной) документа­цией, а неремонтируемый объект - это объект, ремонт которого не возможен и не преду­смотрен этой документацией.

В зависимости от характерных особенностей показатели надёжности подразделяют на несколько типов.

Единичный показатель надёжности - это показатель надёжности, характеризующий одно из свойств, составляющих надёжность объекта.

Комплексный показатель надёжности - это показатель надёжности, характеризующий не­сколько свойств, составляющих надёжность объ­екта.

Расчётный показатель надёжности - это показатель надёжности, значения которого оп­ределяются расчетным методом.

Экспериментальный показатель надёжности - это показатель надёжности, точечная или интер­вальная оценка которого определяется по данным испытаний.

Эксплуатационный показатель надёжности - это показатель надёжности, точечная или интер­вальная оценка которого определяется по дан­ным эксплуатации.

Экстраполированный показатель надёжности - это показатель надёжности, точечная или интер­вальная оценка которого определяется на осно­вании результатов расчетов, испытаний и (или) эксплуатационных данных путем экстраполиро­вания на другую продолжительность эксплуата­ции и другие условия эксплуатации.

В зависимости от оцениваемых свойств, характеризующих надёжность, показатели надёжности подразделяют на:

• 
  показатели безотказности,
  
• 
  показатели долговечности,
  
• 
  показатели ремонтопригодности,
  
• 
  показатели сохраняемости;
  
• 
  комплексные показатели надёжности.
  

3.2.Показатели безотказности

3.2.1 Набор показателей безотказности для различных видов объектов

Для необслуживаемых, невосстанавливаемых и неремонтируемых объектов в качестве показателей безотказности используют вероятность безотказной работы, интенсивность отказов, среднюю наработку до отказа и гамма-процентную наработку до отказа. Для обслуживаемых, восстанавливаемых и ремонтируемых объектов в качестве показателей безотказности используют среднюю наработку на отказ, параметр потока отказов и осреднённый параметр потока отказов.

3.2.2 Вероятность безотказной работы, вероятность отказа и частота отказов

Вероятность безотказной работы - это вероятность того, что в пределах заданной на­работки отказ объекта не возникнет. Вероятность безотказной работы определяется в предположении, что в на­чальный момент времени (момент начала исчисления наработки) объект нахо­дился в работоспособном состоянии.

Обозначим через t время или суммарную наработку объекта (в дальнейшем для краткости называем t просто наработ­кой). Возникновение первого отказа - случайное событие, а наработка τ от начального момента до возникновения этого события - случайная величина. Вероятность безотказной работы P(t) объекта в интервале наработки от 0 до t включительно определяют как

(3.1)

Здесь Ρ{τ > t} - вероятность события, заключенного в скобках. Вероятность без­отказной работы Ρ(t) является функцией наработки t . Обычно эту функцию предполагают непрерывной и дифференцируемой.

Если способность объекта выполнять заданные функции характеризуется одним параметром х, то вместо (3.1) имеем формулу

P(t) = Ρ{х_ниж(t₁) <х(t₁) < х_верх(t₁)}; 0 < t₁ t , (3.2)

где х_ниж(t₁)и х_верх(t₁)- предельные по условиям работоспособности значения парамет­ров (эти значения, вообще, могут изменяться во времени). Аналогично вводят вероятность безотказной работы в более общем случае, когда состояние объекта характеризуется набором параметров с допустимой по условиям работоспособности областью значений этих параметров [14].

Вероятность безотказной работы P(t) связана с функцией распределения F(t) и плотностью распределения f(t) наработки до отказа:

F(t) = 1 - P(t); f(t) = dF(t) / dt = - dP(t) / dt . (3.3)

Наряду с понятием «вероятность безотказной работы» часто используют понятие «вероятность отказа» Q(t), то есть вероятность того, что объект откажет хотя бы один раз в течение заданной наработки, будучи работоспособным в начальный момент времени:

Q(t) = 1 - P(t) = F(t) . (3.4)

Из (3.3) с учётом (3.4) получим:

(3.5)

. (3.6)

Плотность распределения f(t) наработки до отказа в литературе по надёжности называют частотой отказов, хотя в стандарте этот термин отсутствует. Типичная зависимость частоты отказов f от времени (от наработки) t изображена на рисунке 3.1.

Из неё видно, что всё время рабо­ты изделий можно разделить на три участка, соответ­ствующие трём независимым группам отказов. Временной промежуток от 0 до t₁ называется участком приработки. На нем происходят отказы, в основном, из-за дефектов производства. На самом протяжённом основном временном промежутке от t₁ до t₂ выход изделий из строя обусловлен, в основном, внезапными от­казами. Временной промежуток от t₂ до t₃ характеризуется возрастанием частоты отказов из-за деградационных процессов, ухудшающих состояние с точки зрения безотказности (старение и износ изделий). На участке после времени t₃ час­тота отказов уменьшается из-за уменьшения количества исправных изделий. В сложной системе на стадии эксплуатации наряду с деградационными процессами действуют и стабилизирующие про­цессы, обеспечивающие сопротивление развитию деградации, под­держивающие работоспособность устройства или системы в за­данных пределах или восстанавливающие, парирующие ухудше­ние состояния. К стабилизирующим про­цессам относятся та­кие, как автоматическая подстройка и регулировка состояния РЭС при функциональном использовании (автоматическая регули­ровка усиления - АРУ, автоподстройка частоты - АПЧ и др.), а для восстанавливаемых изделий также подстройки, регулировки, замены на этапах технического обслуживания и ремонта (если отказ всё-таки произошел) [3].

Точечные статистические оценки для вероятности безотказной работы P_стат(t), вероятности отказа Q_стат(t) и час­тоты отказов f_стат(t) для наработки от 0 до t даются формулами:

P_стат(t) =1 - n(t) / N, (3.7)

Q_стат(t) = n(t) / N, (3.8)

f_стат(t) = n(∆t) / (N∆t), где (3.9)

N – число объектов, работоспособных в начальный момент времени (наработки); ∆t - промежуток времени (наработки); n(∆t) - число объектов, отказавших в интервале времени (наработки)от t - ∆t / 2 до t + ∆t / 2; n(t) - число объектов, отказавших на отрезке от 0 до t.

Для получения достоверных оценок объем выборки N должен быть достаточно велик [10, 14].

3.2.3 Интенсивность отказов

Показателем, наиболее полно характеризующим надёжность неремонтируемых изделий, является интенсивность отказов.

Интенсивность отказов λ(t) – это условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не возник. Её определяют по формуле

. (3.10)

Для высоконадежных систем Р(t) близко к единице, так что интенсивность отказов приближенно равна плотности распределения наработки до отказа. Преобразуем формулу (3.10), чтобы выразить Р(t) через λ(t). Из формулы (3.10) следует, что

λ(t)dt = - d Р(t) / Р(t). (3.11)

Интегрируя обе части выражения (3.11) в пределах от 0 до t, получим

(3.12)

откуда

(3.13)

Используя начальные условия t = 0 и Р(0) = 1, найдем постоянную С = 0. При этом

(3.14)

Статистическая оценка для интенсивности отказов λ_стат(t) имеет вид

(3.15)

Типичная зависимость интенсивности отказов λ от времени (от наработки) t изображена на рисунке 3.2.

Э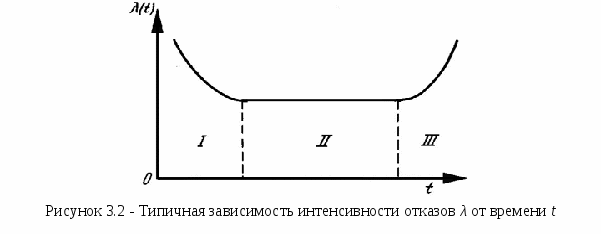
та зависимость имеет те же характерные участки, что и зависимость частоты отказов. На участке нормальной работы изделий, находящемся между участком приработки изделий и участком постепенных износовых отказов, интенсивность отказов λ определяется внезапными отказами и постоянна, то есть не зависит от времени. Для этого участка, на котором изделия работают наиболее долго, формула для расчёта вероятности безотказной работы (3.14) упростится и примет вид:

(3.16)

Это выражение называют экспоненциальным законом вероятности безотказной работы. Его наиболее часто используют для расчета этой вероятности.

3.2.4 Средняя наработка до отказа

Средняя наработка до отказа Т₁ - это математическое ожидание наработки объекта до первого отказа. Её вычисляют по формуле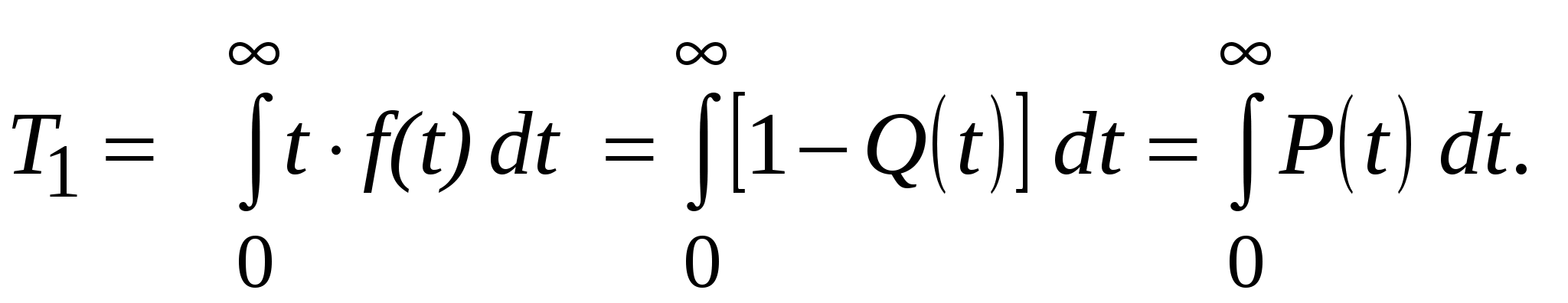

(3.17)

Для второго участка работы (рисунок 3.2), когда интенсивность отказов λ не зависит от времени t, средняя наработка до отказа равна

Т₁ = 1 / λ. (3.18)

Среднее время безотказной работы в интервале 0 ... t при экспоненциальном законе вероятности безотказной работы

. (3.19)

Дисперсия времени безотказной работы

(3.20)

а среднее квадратическое отклонение

(3.21)

Статистическую оценку средней наработки до отказа Т_1стат вычисляют по формуле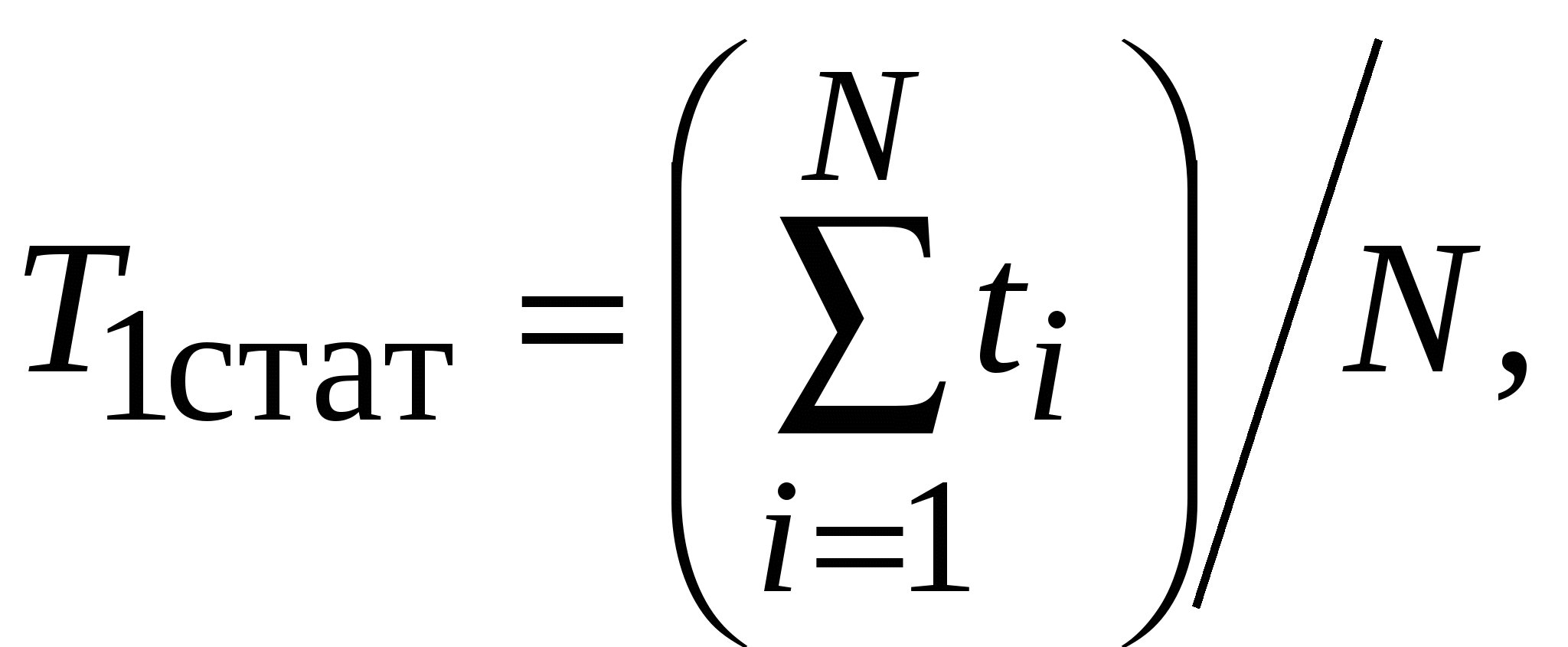

(3.22)

где N - число отказов, про­изошедших за наработку t; t_i - наработка (время) отказа i-ro элемента. Формула (3.22) соответствует плану испытаний, при котором все объекты испы­тываются до отказа [14].

3.2.5 Гамма - процентная наработка до отказа

Гамма - процентная наработка до отказа - это наработка t_γ, в течение которой отказ объекта не возникнет с вероятностью γ, выраженной в процентах. Её определяют как корень t_γ уравнения

F(t_γ) =Q(t_γ) = 1- Р(t_γ) = 1 - γ / 100, (3.23)

где F(t_γ) = Q (t_γ) – функция распределения наработки до отказа (вероятность отказа), а P(t_γ) - вероятность безотказной работы.

Как видно из формулы (3.23), гамма - процентная наработка до отказа равна кванти­ли соответствующего распределения. Если вероятность, отвечающая этой квантили, выражают в процентах, то для показателей безотказности обычно задают значения 90; 95; 99; 99,5% и т.д. Тогда вероятность возникновения отказа на отрезке [0 .. t] будет составлять: 0,10; 0,05; 0,01; 0,005 и т.д. Зада­ваемые значения γ для критических отказов должны быть весьма близки к 100 %, чтобы сделать критические отказы практически невозможными события­ми [14].

3.2.6 Средняя наработка на отказ

Средняя наработка на отказ (наработка на отказ) Т определяется как отношение суммарной наработки восстанав­ливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки.

Этому определению средней наработки на отказ соответствует формула

Т = t/ М{r(t)}. (3.24)

Здесь t - суммарная наработка, r(t) - число отказов, наступивших в течение этой наработки, М{r(t)} - математическое ожидание этого числа. В общем случае средняя наработка на отказ оказывается функцией t. Для стационарных потоков отказов средняя наработка на отказ от t не зависит.

Статистическую оценку средней наработки на отказ Т вычисляют по формуле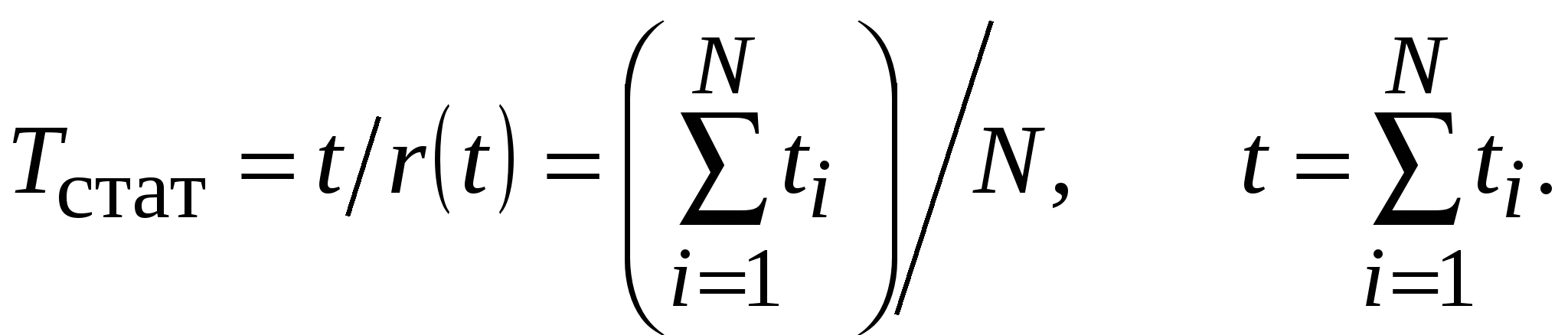

(3.25)

В отличие от формулы (3.24), здесь r(t) = N - число отказов, фактически про­изошедших за суммарную наработку t; t_i - наработка (время) отказа i-гo элемента. Показатель средняя наработка на отказ введен применительно к восстанавливаемым объектам, при эксплуатации которых допускаются многократно повторяющиеся отказы, не приводящие к серьез­ным последствиям и не требующие значительных затрат на восстановление работоспособного состояния. Эксплуатация таких объектов может быть описана следующим образом: в начальный момент времени объект начинает работать, и продолжает работать до первого отказа; после отказа происходит восстановление работоспособности, и объект вновь работает до отказа и т.д. На оси времени моменты отказов образуют поток отказов, а моменты восстановлений - поток восстановлений. На оси суммарной наработки (когда время восстановления не учитывается) моменты отказов образуют поток отказов [14].

3.2.7 Параметр потока отказов и осреднённый параметр потока отказов

Параметр потока отказов ω(t) – это отношение математического ожидания числа отказов восстанавливаемого объекта за достаточ­но малую его наработку к значению этой нара­ботки. Осреднённый параметр потока отказов ω_оср(t) - это отношение математического ожидания числа отказов восстанавливаемого объекта за конечную наработку к значению этой наработки. В стандарте параметр потока отказов обозначен μ(t), но поскольку во всей цитируемой литературе буквой μ обозначена интенсивность восстановления, то во избежание путаницы будем обозначать параметр потока отказов ω(t). Параметр потока отказов ω(t) определяют по формуле

(3.26)

где Δt - малый отрезок наработки, r(t) - число отказов, наступивших от начального момента времени до до­стижения наработки t. Разность представляет собой число отказов на отрезке Δt.

В расчетах при обработке эксперимен­тальных данных часто используют осредненный параметр потока отказов

(3.27)

По сравнению с формулой (3.26) здесь рассматривается число отказов за конечный отрезок (t₂ - t₁), причем t₁ ≤ t ≤ t₂. Если поток отказов стационарный, то параметры ω(t) и ω_оср(t), определяемые по формулам (3.26) и (3.27) от t не зависят.

Статистическую оценку для параметра потока отказов ω_стат(t) определяют по формуле

ω_стат(t) = [r(t₂) - r(t₁)] / (t₂ - t₁), (3.28)

которая по структуре аналогична формуле (3.27). Для стационарных потоков можно применять формулу

ω_стат = 1 / T_стат.. (3.29)

Если время t стремится к бесконечности, на практике выполняется равенство параметра потока отказов интенсивности отказов для второго участка работы (рисунок 3.2), когда λ не зависит от времени

λ(t) = λ = ω(t) = 1 / Т₁. (3.30)

Поэтому для стационарных потоков отказов ремонтируемых объектов, вместо параметра потока отказов часто используют показатель надёжности неремонтируемых объектов - интенсивность отказов λ. Это свойство функции ω(t) отражает тот факт, что с течени­ем времени единый процесс отказов и восстановлений становится стационарным и среднее число отказов не зависит от предшеству­ющей эксплуатации [3].