Теория надежности. Учебное пособие для студентов

• Название: Учебное пособие для студентов
• Анкор: Теория надежности.doc
• Дата: 07.05.2017
• Размер: 3.48 Mb.
• Имя файла: Теория надежности.doc
• Тип: Учебное пособие; #7212
• страница: 6 из 23

3.6.Комплексные показатели надёжности

К комплексным показателям надёжности относятся коэффициенты: готовности, оперативной готовности, технического использования и сохранения эффективности. Все комплексные показатели описывают надёжность восстанавливаемых объектов.

Коэффициент готовности К_Г – это вероятность того, что объект окажется в рабо­тоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается. Различают стационарный и нестационарный коэффициенты готовности, а также средний коэффициент готовности [3].

Выведем выражение для стационарного коэффициента готовности восстанавливаемых объектов. С точки зрения потребителя интерес представляют два состояния таких объектов:

• 
  S₀(t) с вероятностью пребывания P₀(t), в котором система может использоваться по своему назначению,
  
• 
  S₁(t) с ве­роятностью P₁(t) - система использоваться по своему назначе­нию не может.
  

По определению К_г = P₀ – вероятность застать систему в установившемся режиме в исправном состоянии, а К_п = P₁ - вероятность застать систему в этом же режиме в неисправном состоянии. Граф переходов и зависимость состояния от времени такой системы показаны на рисунке 3.3 а и б (слева).

Дифференциальные уравнения для вероятностей состояний объекта можно составить по виду графа состояний, используя инженерное правило, сформулированное академиком А. Н. Колмогоровым [5]: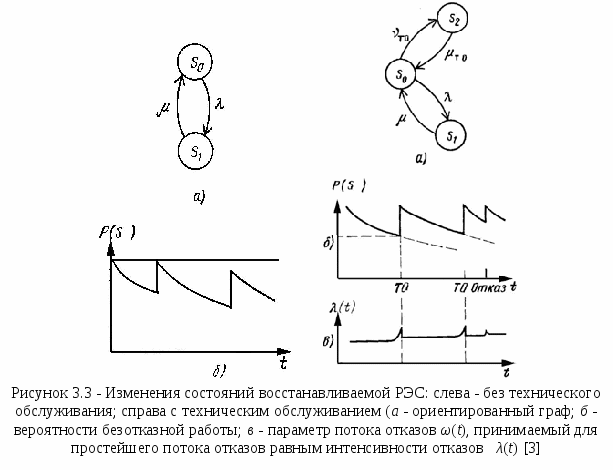


Производная по времени от вероятности P_k(t) пребывания системы в любой момент времени t в состоянии k равна алгебраической сумме произведений интенсивностей переходов в k-ое состояние (или из k-го состояния) на вероятность того состояния, откуда совершается переход в k-е состояние. Причем, тем слагаемым, которым соответствуют уходящие стрелки из k-го состояния приписывается знак “минус”, а входящим - “плюс”.

Кроме того, используется нормировочное отношение

(3.33)

В итоге для нашего примера имеем

dP₀(t) / dt = -λ·P₀(t) + μ·P₁(t); (3.34)

dP₁(t) / dt = λ·P₀(t) - μ·P₁(t); (3.35)

P₀(t) + P₁(t) = 1. (3.36)

С учётом того, что в установившемся режиме P_k не зависит от времени t и dP_к(t) / dt = 0 выражения (3.34) и (3.36) примут вид

0 = -λ·P₀ + μ·P₁; (3.37)

P₀ + P₁ = 1. (3.38)

Из двух последних уравнений имеем

P₀ = (μ / λ)·P₁ = (μ. / λ)·(1- P₀) = (μ / λ) – (μ· P₀) / λ. (3.39)

Откуда

P₀ = (μ / λ) / (1 + μ / λ) = μ / (λ + μ) = К_г; (3.40)

P₁ = 1- P₀ = λ / (μ + λ) = К_п. (3.41)

Учтём, что интенсивности восстановления μ и интенсивности отказов λ определяются выражениями

μ = 1 / Т_в , (3.42)

λ = 1/ Т, (3.43)

где Т_в – среднее время восстановления, а Т - средняя наработка до отказа.

Тогда получим выражения для стационарных коэффициента готовности К_г и для коэффициента простоя К_п:

К_г = Т / (Т + Т_в), (3.44)

К_п = Т_в / (Т + Т_в). (3.45)

Коэффициент оперативной готовности К_ОГ(t) - это вероятность того, что объект окажется в ра­ботоспособном состоянии в произвольный момент времени t, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается, начиная с этого момента, будет работать безотказно в течение заданного интервала времени. При экспоненциальном законе вероятности безотказной работы

К_ОГ(t) = К_Г ехр(- λt). (3.46)

Коэффициент готовности характеризует готовность объекта к применению по назначению только в отношении его работоспособности в произвольный мо­мент времени. Коэффициент же оперативной готовности характеризует надёжность объекта, необходимость применения которого возникает в произвольный момент времени, после которого требуется безотказная работа в течение заданного интервала времени.

Нестационарный коэффициент готовности k_Г(t), называемый также функцией готовности - это вероятность того, что объект окажется в рабо­тоспособном состоянии в заданный момент времени, отсчитываемый от начала работы (или от другого строго определённого момента времени). Иными словами, вероятность k_Г(t) пребывания системы в состоянии готовно­сти к функциональному применению называется функцией готов­ности [19, 21]:

(3.47)

При t→ ∞

k_Г(t) = К_г. (3.48)

Средний коэффициент готовности - это усреднённое на данном интервале времени значение нестационарного коэффициента готовности [21].

Восстановительные работы могут состоять из работ по техническому обслуживанию (ТО) работоспособного, хотя и неисправного, изделия и ремонта отказавшего изделия. Пребывание изделия в этих состояниях учитывается и оценивается с помощью коэффициента технического использования - К_ТИ. Коэффициент технического использования характеризует долю продолжительности нахождения объекта в работоспособном состоянии относительно общей продолжительности эксплуатации [3, 14].

Выведем выражение для коэффициента технического использования восстанавливаемых объектов. Граф переходов и зависимость состояния от времени такой системы показаны на рисунках 3.3 а и б (справа). Дифференциальные уравнения для вероятностей состояний объекта составим по виду графа состояний, используя инженерное правило А. Н. Колмогорова. Кроме того, запишем нормировочное отношение (3.29). В итоге получим:

dP₀(t) / dt = -P₀(t)(λ +Ʋ_ТО) + μР₁(t) + μ_ТОР₂(t); (3.49)

dP₁(t) / dt = λ·P₀(t) – μP₁(t); (3.50)

P₀(t) + P₁(t) + Р₂(t) = 1. (3.51)

Здесь: интенсивности восстановления μ и интенсивности отказов λ определяются выражениями (3.42) и (3.43); интенсивность μ_ТО связана со средней продолжительностью ТО (Т_ТО), а интенсивность Ʋ_ТО - с периодом времени между предыдущим и последующим ТО (τ_ТО) зависимостями

Т_ТО = 1 / μ_ТО, (3.52)

τ_ТО = 1 / Ʋ_ТО. (3.53)

При t → ∞ с учетом стационарности наблюдаемого случайного процесса имеем [3]:

К_ТИ = Т / [Т + Т_В + Т_ТО(Т / τ_ТО)]. (3.54)

Оптимальный период времени между предыдущим и последующим ТО, в котором минимизируется величина коэффициента простоя К_П, находят по формуле [5]:

τ_{ТО ОПТ} = (2Т_ТОТ)^0,5 . (3.55)

Однако в литературе коэффициент технического использования К_ТИ часто рассчитывают как отно­шение математического ожидания времени пребывания объекта в работоспособном состоянии за некоторый период эксплуатации к сумме математических ожиданий интервалов времени пребывания изделий в работоспособном состоянии и простоев, обусловленных техническим обслуживанием и ремонтом за тот же период:

К_ТИ = Т / (Т + Т_В + Т_ТО), (3.56)

то есть принимают отношение (Т / τ_ТО) в формуле (3.54) равным единице.

В процессе технического обслуживания также должно осуще­ствляться полное или частичное обновление системы, что зафик­сировано на графиках рисунков 3.3 б и в (справа) зависимостями Р(t) и λ(t). Однако в современных сложных РЭС отказ элемента или РЭУ не всегда ведет к отказу системы и с этой точки зрения являет­ся дефектом. В процессе эксплуатации возникает необходимость выявления дефектов и предотвращения отказов. Эффективность этого процесса можно характеризовать вероятностью отсутствия дефекта в произвольный момент времени при, нахождении РЭС в рабочем состоянии - коэффициентом отсутствия дефектов [3]:

(3.57)

где P_К(t) - представляется суммарной вероятностью пребывания РЭС в подмножестве К состояний, включающем в себя все ситуа­ции, когда в рабочем режиме отсутствуют дефекты.

Коэффициент сохранения эффективности - это отношение значения показателя эффективно­сти использования объекта по назначению за оп­ределенную продолжительность эксплуатации к номинальному значению этого показателя, вычисленному при условии, что отказы объекта в те­чение того же периода не возникают. Коэффициент сохранения эффективности характеризует степень влияния отказов объекта на эффективность его применения по назначе­нию. Для каждого конкретного типа объектов содержание понятия эффектив­ности и точный смысл показателя (показателей) эффективности задаются тех­ническим заданием и вводятся в нормативно-техническую и (или) конструк­торскую (проектную) документацию [14].
3.7.Распределения Пуассона, Эрланга и временные зависимости показателей надёжности для законов распределения наработки на отказ, характерных для участка приработки и участка постепенных износовых отказов

3.7.1 Распределение Пуассона

Распределение Пуассона, которым описывают поведение дискретных случайных величин, применимо для оценки надёжности ремонтируемых изделий с простейшим потоком отказов, называемым стационарным пуассоновским потоком. Простейшие потоки это потоки, обладающие свойствами ординарности, стационарности и отсутствия последствия. Ординарность потока означает, что вероятность появления двух и более событий в один и тот же момент равна нулю. Стационарность потока означает, что вероятность попадания любых событий в промежуток от времени t до времени t + ∆t не зависит от t, а зависит только от длины участка ∆t. Отсутствие последствия заключается в том, что для двух отрезков времени ∆t₁ и ∆t₂ число событий, попадающих в один из них, не зависит от числа событий, попадающих в другой.

Случайная величина t распределена по закону Пуассо­на, если вероятность того, что она примет определенное значение К на отрезке [0 .. t] выражается формулой [3]:

Ρ_К(К, t) = (а^К / К!) ехр(-а), (3.58)

где а - параметр закона Пуассона (математическое ожидание случайной величи­ны t).

Дисперсия случайной величины t,распределенной по закону Пуас­сона, равна ее математическому ожиданию:

D_t = a.(3.59)

Вид распределения Пуассона при различных значениях а показан на рисунке 3.4, а. Интервалы времени между отказами в пуассоновском потоке отказов взаимозависимы и распределены по экспоненциаль­ному закону. Среднее число отказов в интервале [0 .. t] для пуассоновского потока

а = λ t. (3.60)

Параметр пуассоновского потока отказов

ω(t) = λ, (3.61)

то есть совпадает с интенсивностью отказов экспоненциального распределения.

Если время безотказной работы изделия подчиняется экспонен­циальному закону, то поток отказов восстанавливаемого РЭС яв­ляется пуассоновским и вероятность появления К от­казов на отрезке [0 .. t] определяется формулой Пуассона:

Q(К, t) = [(λ t)^К / К!] ехр(-λ t). (3.62)

Если время безотказной работы каждого элемента велико и подчиня­ется экспоненциальному закону распределения, то поток отказов системы, как сумма N простейших потоков, также является простейшим и имеет суммарную интенсивность

(3.63)

П
ри этом должно выполняться условие, что доля каждого элемента в фор­мировании общего потока отказов мала [3].

3.7.2 Нормальное распределение времени безотказной работы при постепенных отказах и учёт влияния этих отказов при расчёте надёжности

Рас­пределение времени безотказной работы до появления постепенного (износового) отказа (на третьем участке рисунка 3.2) в большинстве практических ситуаций, когда все отказы однородны по качеству и имеют малый разброс по времени возникновения, близко к нормальному, то есть хорошо описывает­ся законом Гаусса (рисунок 3.4, б). При отрицательных значениях величины наработки до отказа t плотность распределения наработки до отказа f(t) равна нулю

f(t) = 0, t ≤ 0; (3.64)

В этом случае количественные показатели надёжности имеет смысл рассматривать только при усеченном гауссовском распределении, когда плотность распределения наработки до отказа равна [1]

(3.65)

где σ² и Т₀ – соответственно дисперсия и среднее значение (математическое ожидание) случайной величины t, а с - постоянная усеченного нормального распределения, равная

(3.66)

которая находится из условия нормировки

- табулированные значения интеграла вероятности (нормированной функции Лапласа). Таблица Р_Д(t) = 2Ф(t) (таблица 7.6) приведена в разделе 7;

(3.67)

Нормированная функция Лапласа является нечётной

Ф(-t) = -Ф(t). (3.68)

Вероятность безотказной работы системы определяется по формуле

(3.69)

Интенсивность отказов λ(t), с учётом выражений (3.10), (3.65) и (3.69), определяют по формуле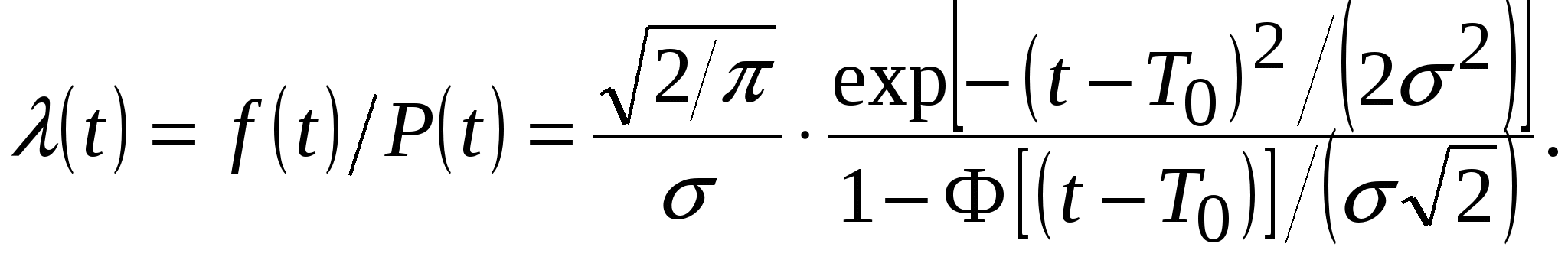

(3.70)

Среднюю наработку до отказа определяют по формуле [1]

Т_{1стат ус} = Т₀ + σf₁(Т₀ / σ), (3.71)

где f₁(Т₀ / σ) имеет тот же физический смысл, что и f(t) [см. формулу (3.65)].

Непосредственно нормальный закон распределения для расчета показателей безотказности может применяться только в случае, если

Т₀ >> σ. (3.72)

В этом случае постоянная с и средняя наработка до отказа Т_1стат равны

, Т_1стат = Т₀. (3.73)

Безусловная вероятность отказа изделия на временном интер­вале от t₁ до t₂ в этом случае равна [4]

(3.74)

Если условие (3.72) не выполняется, то нормальная плотность распределения (3.65) не является односторонней, т.е. она отлична от нуля и при t < 0. При Т_1стат >> σ этот недостаток практически не сказывается, так как в этом случае частью кривой распределения при t < 0 можно пренебречь. Однако если условие (3.72) не выполняется, то использование нормального распределения может привести к заметным погрешностям. Поэтому на практике используют усеченное нормальное распределение (рисунок 3.4, в). Для этого отсекают часть кривой распределения при t < 0 и вводят с нормирующий множитель с, рассчитываемый по формуле (3.66) чтобы сохранить условия нормирования плотности вероятности [4].

Пример 3.1 [1].

Известно, что исследуемая неремонти­руемая РЭС имеет нормальное распределение наработки до отказа с парамет­рами Т₀ = 520 ч и σ = 150 ч. Требуется определить вероятность безотказной рабо­ты РЭС при наработке t = 400 ч и ее интенсивность отказов.

Решение. Из (3.69) следует, что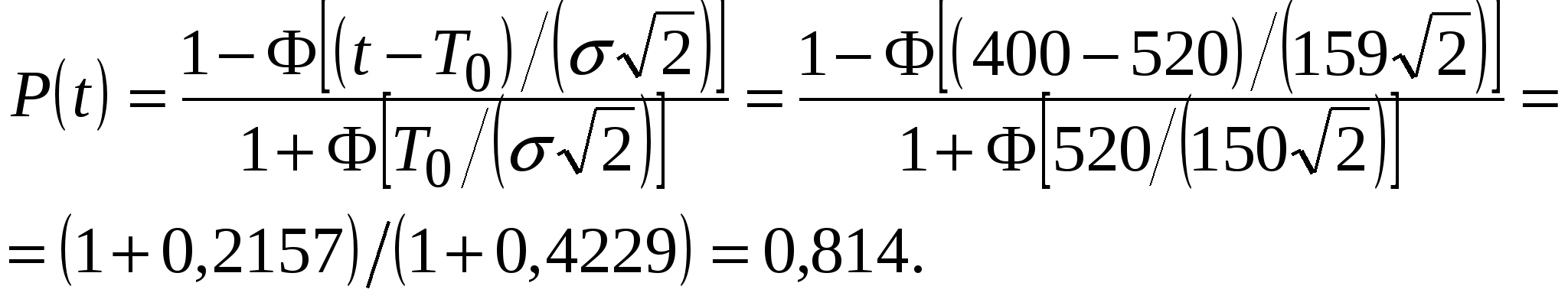



Значения функций Лапласа Ф(t) =0,5Р_Д(t) находим из таблицы 7.6, приведенной в разделе 7: Φ(0,5657) = 0,2157 и Ф(2,4513) = 0,4929. Знак плюс в числителе P(t) появился потому, что функция Ф(t) нечетная, т.е. Ф(-0,5657) = -0,2157. Из (3.70) следует, что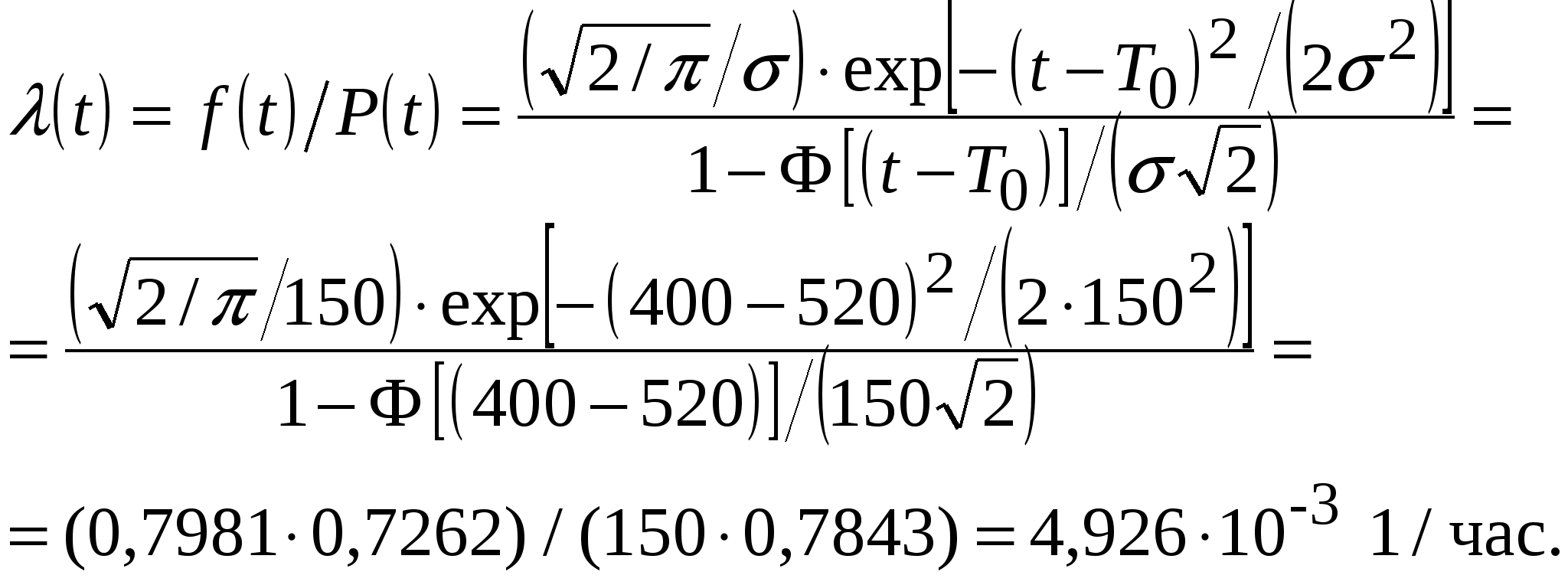



Рассмотрим в общих чертах учёт влияния постепенных отказов при расчёте надёжности для нормального распределения времени безотказной работы [7].

Пусть случайное изменение значения выходного параметра У в партии изделий происходит, например, в сторону его уменьшения во времени τ (рисунок 3.4). Полная вероятность безотказной работы P_П(τ) (по внезапным и постепенным отказам) в момент времени τ определяется по формуле

(3.75)

где P(τ) - вероятность безотказной работы системы по внезапным отказам, рассмотренная в разделе 3.2.2; N - число учитываемых выходных параметров системы, изменение которых во времени может привести к её отказу; P_постi(τ) - вероятность безотказной работы системы по постепенным отказам, связанным с выходом i-го выходного параметра за пределы допустимых значений и возникающим из-за деградационных процессов старения и износа. Так как выход параметра изделия за границы α или β поля считается параметрическим отказом, то вероятность P_постi(τ) называют параметрической надёжностью.

Распределение времени пересечения границы поля допуска реализациями случайных функций, представляющих изменения выходных параметров конкретных изделий во времени - кривая У(τ), характеризует параметрическую надёжность данного типа изделия. Параметрическая надёжность определяется плотностью распределения У(τ) и представляет собой вероятность того, что время непрерывной работы τ_Р изделия будет больше заданного времени τ_ЗАД при условии, что выходной параметр останется в пределах поля допуска:

P_{пост i}(τ) = вер(τ_Р > τ_ЗАД ) при β ≥ У_i ≥ α. (3.76)

Распределение f(У) выходных параметров изделий У в партии в поле допуска характеризует динамическую точность изделий в рассматриваемый момент временя τ. Под динамической точностью D_У понимают вероятность нахождения параметра У изделия в пределах допуска в момент времени τ

D_У(τ) = вер(β ≥ У_i ≥ α, τ). (3.77)

Если распределение выходного параметра У подчиняется усеченному нормальному закону распределения, то динамическая точность определяется выражением:

(3.78)

где У_СР (τ) - среднее значение выходного параметра распределения в момент времени τ; σ_У(τ)- среднеквадратичное отклонение выходного параметра У в момент времени τ; С_Н - нормирующий множитель, определяемый по аналогии с формулой (3.73) выражением:

С_Н = Ф[У_СР(τ)] / σ_У(τ). (3.79)

Значения У_СР(τ) и σ_У(τ) определяются путем расчета допусков для партии изделий с учетом старения.

На рисунке 3.5 видно, что в моменты времени τ₂ и τ₃ имеются отказавшие изделий (заштрихованные площади распределений в соответствующих сечениях τ₂ и τ₃ случайного процесса). Расчет параметрической надёжности ведется через динамическую точность [7]. Так как и этот расчет, и учёт в нём процессов деградации сложно осуществлять, то обычно ограничиваются расчетом надёжности изделий по внезапным отказам. Если же параметрическую надёжность учитывать всё же необходимо, то её запас можно оценить по рез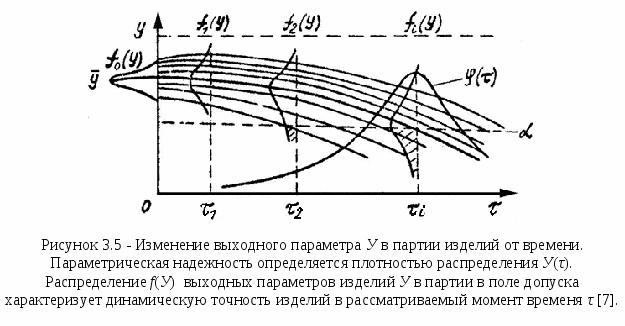
ультатам граничных испытаний, описанных в разделе 6.7.

3.7.3 Распределение времени безотказной работы по закону Релея

Распределение времени безотказной работы по закону Релея (рисунок 3.6, а) достаточно полно описывает поведение ряда изделий с явно выраженным эффектом старения и износа. Зависимости вероятности безотказной работы P(t), интенсивности отказов λ(t) и частоты отказов f(t) для этого закона определяются выражениями [4]:

f(t) = (t / С²)ехр[-t ² / 2С²]; (3.80)
Ρ(t) = ехр[ - t² / 2С²]; (3.81)
λ(t) = t / С² ; (3.82)

(3.83)

где С – параметр распределения.

3.7.4 Распределение времени безотказной работы по закону Вейбулла

Распределение Вейбулла (рисунок 3.6, б) достаточно хорошо описывает распределение отка­зов в объектах, содержащих большое количество однотипных неремон­тируемых элементов (ЭВП, полупроводниковые приборы, микромо­дули и др.). Зависимости вероятности безотказной работы P(t), интенсивности отказов λ(t) и частоты отказов (f(t) для этого закона определяются выражениями [4]:

f(t) = λ ₀bt ^b-1ехр[-λ₀ t^b]; (3.84)
Ρ(t) = ехр[-λ ₀  t^b], t ≥ 0; λ₀ > 0; b > 0; (3.85)
λ(t) = λ₀ b t^{b -1}; (3.86)

Т₁ = λ₀^{–1 / b}  Г(1 + 1 / b), (3.87)

где Г(1 + 1 / b) - табулированная полная гамма-функция.

Ч
асто поведение РЭА на первом участке эксплуатации (см. рисунок 3.1) хорошо описывается законом распределения Вейбулла с b < 1, на втором участке - экспоненциальным законом, а на третьем - нормальным распределением, распределением Релея или распределением Вейбулла с b > 1. Для стратегии ТО по состоянию особенно важно определение поведения РЭА в начале третьего участка эксплуатации.

3.7.5 Законы распределения времени ремонта

Если аппаратура модульного типа и ремонт осуществляется заменой модуля, то имеет место экспоненциальный закон распределения вре­мени ремонта:

f(t_ρ) = (1 / Т_р)ехр(-t_ρ / Т_р); (3.88)

F( t_ρ) = 1 - exp(-t_ρ / T_p), (3.89)

где T_p – среднее вре­мя ремонта.

Для экспоненциального распределения среднеквадратическое отклонение σ_ρ = Т_р. В случаях, когда поиск отказов проводится вручную, закон распре­деления времени текущего ремонта отличен от экспоненциального и, как правило, время ремонта распределено по закону Эрланга (рисунок 3.6, в) [4]:

f(t_ρ) = (4t_ρ / T_p²)exp(-2 t_ρ / T_p); (3.90)

F(t_ρ) = 1 - (1 + 2 t_ρ / T_p)exp(-2 t_ρ / T_p). (3.91)

Для распределения Эрланга среднеквадратическое отклонение σ_ρ ≈ 0,707 Т_р.