1_Вычисления в Excel. Учебное пособие Набережные Челны 2003 г
 Скачать 7.26 Mb. Скачать 7.26 Mb.
|
3. ВычисленияВ этой главе предлагается освоить арифметические и логические выражения, функции Excel и научиться проектировать рабочие книги для вычислений. 3.1. Алгебраические формулы Ввод формул рассматривался в главе 2 (стр.7). В этой главе уделяется внимание правилам написания сложных формул. Прежде чем приступить к выполнению упражнений, рекомендуется переименовать первый лист рабочей книги на имя "Формулы". Затем научиться присваивать имена ячейкам и таблицам для наглядности формул. И  мя - это легко запоминающийся набор символов2, который можно использовать для ссылки на ячейку, блок, формулу. мя - это легко запоминающийся набор символов2, который можно использовать для ссылки на ячейку, блок, формулу. Любой ячейке или блоку можно присвоить текстовое имя, отражающее смысл записанной информации. Ссылка с помощью имени сохраняется на всех листах рабочей книги. Создание имени объекта:
список имён вызывается двумя способами:
Удалить имя объекта - команда Вставка/Имя/ Присвоить, указать в списке удаляемое имя, Удалить. Упражнение 3.1.1. Ввести серию формул, зависящих от двух аргументов: x и у.
Для этого нужно выполнить следующее:
появится адрес В1,
Поместить в В1 число 4, а в В2 число 3.
=(1+X)/(4*Y). При этом учесть следующие правила:
операций в Excel (рис.2.);
В ячейке ВЗ выводится результат 0.416667. Примечание: Формулу можно было ввести и без использования имен: =(1+B1)/(4*B2). У  пражнение 3.1.2. пражнение 3.1.2.Вычислить 25% от числа х (ячейка В1) Решение: = 25%*х (=25%*В1) Рис.2. Приоритет выполнения арифметических операций в Excel. Задача 3.1.
Результат: - 5.93548.
3.2. Использование функций Д  ля выполнения упражнений перейти на второй лист текущей рабочей книги и переименовать лист, присвоив ему имя "Функции". ля выполнения упражнений перейти на второй лист текущей рабочей книги и переименовать лист, присвоив ему имя "Функции".Функции используются для быстрого и эффективного выполнения сложных, но стандартных вычислений.  кнопка Функция, как правило, содержит переменную часть – аргументы. Аргументы могут быть разного типа у разных функций, их может быть много или не быть вовсе. Аргументы – это исходные данные, которые используются функцией для получения результата. Использование Мастера функций существенно облегчает ввод функций.
В Кнопка (Справка) в диалоге Мастера функций дает подробное описание выделенной функции, её аргументов. Здесь же приводятся примеры применения функции. Список соответствия между русскими и английскими названиями функций имеется в файле FUNCS.XLS, который находится в папке C:\Program Files\ Microsoft Office\0ffice. Из этого файла также есть выход к справке по функциям и примеры. Использование панели формул для ввода и изменения формул. О  тобразить панель формул - нажать кнопку Изменить формулу (=) слева от строки ввода. Рис.3. Использование панели формул. С помощью панели формул можно легко вставить функцию в формулу – открыть список функций и выбрать нужную. Если функция отсутствует в списке, для вывода дополнительного списка функций следует выбрать строку «Другие функции». После вставки функции в панели формул отображается имя функции и ее аргументы, описание функции и аргументов, а также возвращаемое функцией и формулой значение. Кроме того, панель формул можно использовать для изменения функции в формуле. Для этого достаточно указать курсором имя функции в строке формул и щелкнуть кнопку Изменить формулу (=). Появляется окно ввода аргументов этой функции, в котором можно произвести необходимые изменения. Упражнение 3.2.1. В ячейку А1 ввести формулу: tg x. З  десь и далее в качестве аргумента x вводится число из ячейки В1 листа "Формулы" (см. упр. 3.1.1 главы 2). десь и далее в качестве аргумента x вводится число из ячейки В1 листа "Формулы" (см. упр. 3.1.1 главы 2).
  Примечание. Обозначение функций в математике и соответствующие им имена в Excel различаются, например: матем. Excel матем. Excel Примечание. Обозначение функций в математике и соответствующие им имена в Excel различаются, например: матем. Excel матем. Exceltg x - TAN(x) |x| - ABS(x) arcsin x - ASIN(x) ln x - LN(x) arccos x - ACOS(X) lg x - Log10(x) arctg x - ATAN(x) ex - EXP(x) Упражнение 3.2.2.В ячейку А2 ввести формулу: tg2 x. При этом следует учесть, что функция в формуле обладает наивысшим приоритетом. Поэтому правильным будет решение: = TAN(x)^2, ошибочно: = TAN^2 (x). З 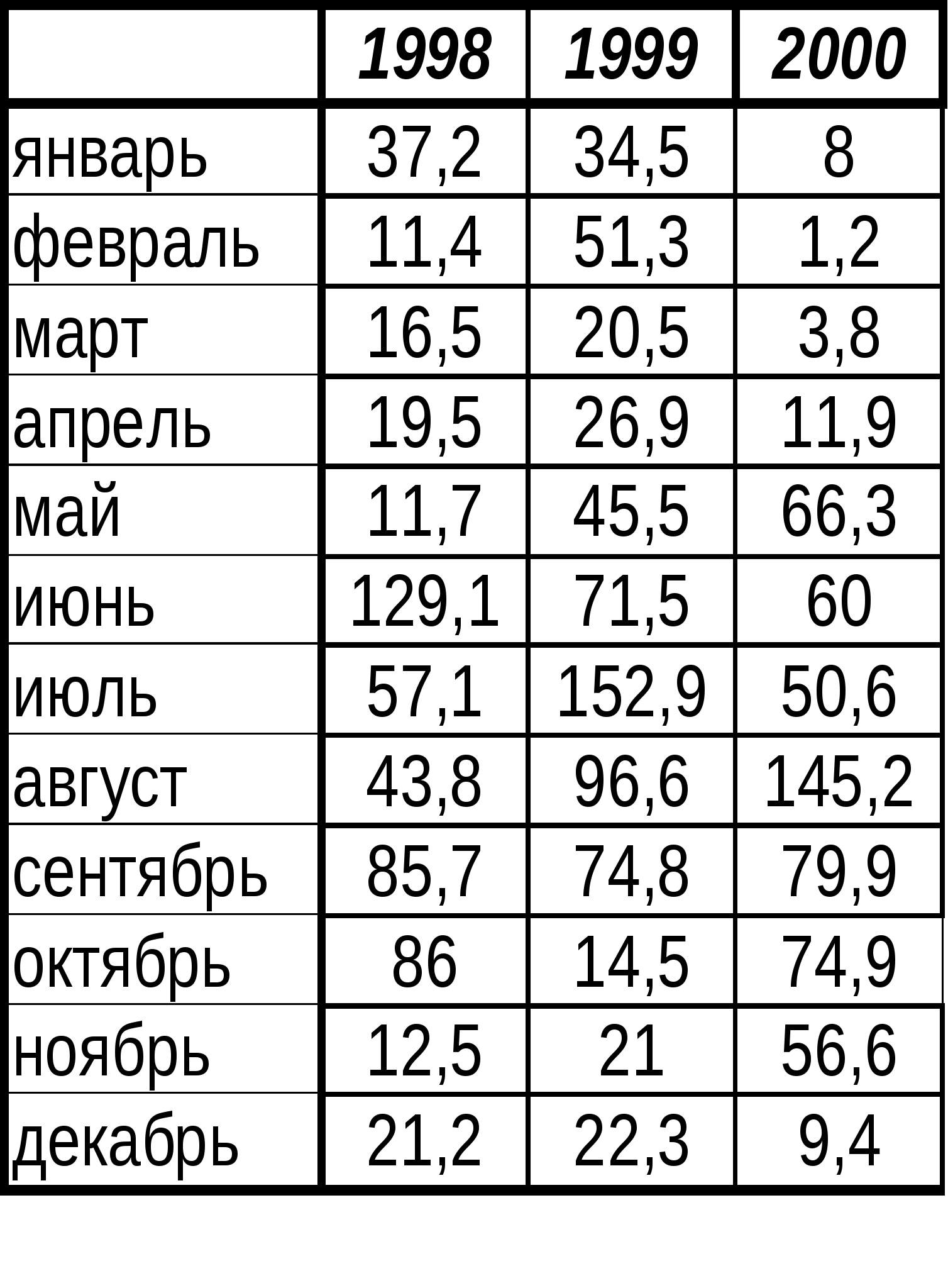 адача 3.2.1. Имеются данные о месячном количестве осадков (в мм) по наблюдениям метеостанции за три года. Подсчитать суммарное, максимальное, минимальное и среднемесячное количество осадков за каждый год и за три года. Подсчитать стандартное отклонение от среднего по годам. адача 3.2.1. Имеются данные о месячном количестве осадков (в мм) по наблюдениям метеостанции за три года. Подсчитать суммарное, максимальное, минимальное и среднемесячное количество осадков за каждый год и за три года. Подсчитать стандартное отклонение от среднего по годам.Рекомендации.
(вызвать список имен - F3).
Упражнение 3.2.3. Вычислить: Эта функция представляет собой комбинацию двух функций: y = Соответствующие функции Excel: KOPEHb(z) и TAN(x)+1. Порядок действий:
Внимание! Не следует щёлкать кнопку "ОК", как обычно — это досрочно завершит ввод формулы. Вместо этого установить в поле ввода курсор на функции КОРЕНЬ(т.е. на внешней функции). Тотчас второе окно Мастера функций для TAN заменится на второе окно для функции КОРЕНЬ.
Окончательная формула в строке ввода: = КОРЕНЬ (TAN(x)+1). Результат = 1.468952. Примечание. Функции можно вводить в строке ввода вручную, причем имена функций следует вводить строчными буквами, например: =корень(tan(x)+1). Если введены имена функций правильно, то по завершении ввода они автоматически будут преобразованы в прописные буквы. Задача 3.2.2. В Excel имеется функция ПИ(), она не имеет аргументов (хотя скобки обязательны) и возвращает число Каким образом вычислить в Excel число е = 2.71828... — основание натуральных логарифмов, если функция, аналогичная ПИ(), для числа е отсутствует? Задача 3.2.3. Что больше: е 3.3. Функции округления В бухгалтерских расчетах большую роль играют функции, позволяющие округлять результаты вычислений. В Excel их несколько, все из категории "Математические".
Между функциями ЦЕЛОЕ и ОСТАТ имеет место соотношение: n = d*ЦЕЛОЕ (n/d) + ОСТАТ (n,d)
Упражнение 3.3.1. В ячейке А1 записано число 143,3184.
Результат - число 143,32.
Р  езультат: число 143. езультат: число 143.
Результат - число 140.
ОКРУГЛВНИЗ (число, число_разрядов), ОКРУГЛВВЕРХ (число, число_разрядов). В соответствии с их названиями они работают как функция ОКРУГЛ, но округляют всегда в большую или меньшую сторону. Рассмотрите примеры самостоятельно. Примечание.
Упражнение 3.3.2. В ячейке А1 записано целое число, лежащее в промежутке от 0 до 999. В ячейку В1 ввести формулу, которая вычисляет сумму цифр числа. ( Пример: для числа 143 сумма цифр = 1+4+3 = 8 ) Ответ: ЦЕЛОЕ(A5/100)+ЦЕЛОЕ(ОСТАТ(A5/10;10))+ОСТАТ(A5;10) (сотни) (десятки) (единицы) Упражнение 3.3.3. Имеется выручка от реализации продукции в сумме 21 675 рублей. Рассчитать налог на пользователей автодорог 2,5%, в том числе федеральный 0,5% и московский 2%. Решение: А В С D
Задача 3.3.1. Идет к -я секунда суток (записана в В3). Сколько полных часов h от 0 до 23 (в В4), полных минут m от 0 до 59 (в В5) и секунд s от 0 до 59 (в В6) прошло к этому моменту. (Пример: k = 13257 = 3*3600+40*60+57, т.е. h = 3, m = 40, s = 57.) Задача 3.3.2. В ячейке А2 записано положительное число. Поместить в В2 формулу, которая возвращает первую цифру из дробной части числа. (Пример: для числа 32.597 формула вернет 5.) Ответ: = ЦЕЛОЕ((A2-ЦЕЛОЕ(A2))*10). 3.4. Логические функции Для использования логических функций следует вспомнить некоторые простые факты из математической логики. Для работы с упражнениями перейти на новый рабочий лист. Дать ему имя "Логика". Упражнение 3.4.1. Логические выражения.
П  равые части обеих формул представляют собой высказывания. равые части обеих формул представляют собой высказывания.
Ввести в А4 число 6. Формула возвращает значение ИСТИНА. В В4 записан предикат.  С пример: b2 > 4ac  равнение двух арифметических выражений, содержащих переменные, даёт предикат. равнение двух арифметических выражений, содержащих переменные, даёт предикат. Высказывание и предикат имеют общее название — логическое выражение. Логические операции - операции, которые объединяют сложные логические выражения. Логические операции реализованы в Excel как функции.
Рис. 4. Перечень логических операций и соответствующих им функций Excel. У  логических функций аргументы могут принимать только два значения: ИСТИНА и ЛОЖЬ. Поэтому логические функции можно задать таблицей, где перечислены все возможные значения аргументов и соответствующие им значения функций. Такие таблицы называются таблицами истинности. логических функций аргументы могут принимать только два значения: ИСТИНА и ЛОЖЬ. Поэтому логические функции можно задать таблицей, где перечислены все возможные значения аргументов и соответствующие им значения функций. Такие таблицы называются таблицами истинности.Таблица для функции НЕ :
Таблица для функций И и ИЛИ имеет вид :
Ф 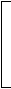 ункция И – логическое умножение - объединяет два или более логических выражения. Выдаёт результат ИСТИНА, если все условия (логические выражения) выполняются совместно (одновременно), и ЛОЖЬ, если хотя бы одно не выполняется. ункция И – логическое умножение - объединяет два или более логических выражения. Выдаёт результат ИСТИНА, если все условия (логические выражения) выполняются совместно (одновременно), и ЛОЖЬ, если хотя бы одно не выполняется. Общий вид функции: И(лог_выражение1; лог_выражение2;…и т.д.) Упражнение3.4.2. Принадлежит ли значение ячейки А1 диапазону чисел [10 ,100] ? Решение:И (А1 >= 10; А1 <=100) Ф 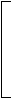 ункция ИЛИ – логическое сложение - предлагает выбрать или одно, или другое из нескольких условий (логических выражений). Результат будет ИСТИНА, если хотя бы одно условие выполняется (имеет значение ИСТИНА), и ЛОЖЬ, если ни одно из условий не выполняется, все ложны. ункция ИЛИ – логическое сложение - предлагает выбрать или одно, или другое из нескольких условий (логических выражений). Результат будет ИСТИНА, если хотя бы одно условие выполняется (имеет значение ИСТИНА), и ЛОЖЬ, если ни одно из условий не выполняется, все ложны.Общий вид функции: ИЛИ (лог_выражение1; лог_выражение2;…и т.д.) Упражнение 3.4.3. Находятся ли значения ячейки А1 вне диапазона чисел [10 ,100] ? Решение:ИЛИ (А1 < 10; А1 >100)  Рис.5. Иллюстрация к упражнениям 3.4.2 и 3.4.3. Если учесть то, что лучи [-∞,10] и [100, ∞] дополняют отрезок [10,100] до полной числовой оси, то можно воспользоваться функциями НЕ и И для определения ИЛИ: ИЛИ (А1 < 10; А1 >100) ≡ НЕ (И (А1 >= 10; А1 <=100)) и наоборот. На практике логические выражения используются в сочетании с функцией ЕСЛИ, являясь первым аргументом её. и  спользуется для проверки содержимого ячейки и возврата логического значения ИСТИНА или ЛОЖЬ. спользуется для проверки содержимого ячейки и возврата логического значения ИСТИНА или ЛОЖЬ.Если возвращаемое значение ИСТИНА, выполняется оператор1, иначе - оператор2: ЕСЛИ (логическое выражение; оператор1;оператор2) Упражнение 3.4.4.
=ЕСЛИ(А1>В1; А1;В1).
Варианты решения: Функция результат
Примечание. Чтобы вернуться из вложенной функции во внешнюю функцию, нужно в строке формул щёлкнуть по имени внешней функции. Упражнение 3.4.5. Выписать счета клиентам по заданным условиям (см. стр.34 - а),b)). Выполнить запросы - c) f). А B C D E
Рис.6. Таблица расчётов с клиентами для случая (а).
(двумя способами - с функциями И и ИЛИ); Решение:
=ЕСЛИ(И(D5>=750;D5<=800);"да";"нет"), скопировать в F6 : F9.
=ЕСЛИ (ИЛИ(D5<750;D5>800);"нет";"да") скопировать в G6 :G9. Сравнить результаты.
=СЧЁТ(C5:C9) (категория статистические)
=СЧЁТЗ(A5:A9) (категория - статистические) В чем отличие функций СЧЁТЗ и СЧЁТ? Прочитайте об этом в справке функций.
=СЧЁТЕСЛИ(E5:E9;«да») (категория - статистические)
=СУММЕСЛИ(E5:E9;«да»;D5:D9) (математические) Задача 3.4.1. Задать ячейкам А2, В2 и С2 имена и, v, w. В ячейках содержатся числа. Ввести в ячейки А3, А4 и т.д. логические формулы, которые возвращают значение ИСТИНА тогда и только тогда, когда а) каждое из чисел и, v, w является положительным; б) хотя бы одно из чисел и, v, w является положительным; в) только одно из чисел и, v, w является положительным; г) ни одно из чисел и, v, w не является положительным; д) хотя бы одно из чисел и, v, w не является положительным. Задача 3.4.2. Ввести в ячейку с именем z любое число. Если z>50, то в ячейке B5 выводить сообщение "Превышено пороговое значение!", иначе выводить z. Задача 3.4.3. Если z [10,25], то возвращать z; если z <10, то возвращать 10; если z > 25, то возвращать 25. Задача 3.4.4. Торговый агент получает процент от суммы совершенной сделки: если объем сделки до 3000, то 5%; если объем до 10 000, то 2%; если выше 10 000, то 1,5%. Введите в ячейку А10 текст "Объем сделки", в ячейку А11 — "Размер вознаграждения". В ячейку В10 введите объем сделки, а в В11 — формулу, вычисляющую размер вознаграждения. Задача 3.4.5. Дать решение примера 3.4.4.(с) (о принадлежности точки отрезку или одному из двух лучей) без использования функций И, ИЛИ, НЕ, а с помощью вложенных функций ЕСЛИ. Задача 3.4.6. В трех ячейках записаны числа. Если все они ненулевые, вернуть 1, в противном случае - 0. Решить задачу с использованием только одной функции ЕСЛИ (без вложений). Задача 3.4.7. Проверить, что вернёт функция ЕСЛИ, когда опущен третий аргумент функции, а условие в первом аргументе ложно? Когда опущен и второй аргумент? Как исправить такую ошибку в цепочке формул? Задача 3.4.8. Вычислить сумму цифр трехзначного числа. Если число (в ячейке с именем п) не является целым или не лежит в промежутке от 0 до 999, то формула возвращает сообщение об ошибке #Н/Д, иначе — возвращает сумму цифр. Задача 3.4.9. Найти действительные корни квадратного уравнения x2 + px + q = 0 по заданным коэффициентам p и q. Если действительных корней нет, вывести об этом сообщение. Лабораторная работа № 2 по теме "Вычисления" Задание. Даны три стороны треугольника а, b, с. Вычислить элементы треугольника:
где р — полупериметр,
(р-с)).
тей. - В ячейки А10 и А11 ввести г и R, а в В10 и В11 — соответствующие формулы.
ранее (кнопка "Формат по образцу).
Сервис/ Зависимости/Влияющие ячейки. Обратить внимание на синие стрелки от ячеек, содержащих длины сторон и площадь треугольника, к ячейке В10.
Стороны 10, 4, 5 не образуют треугольника, при вычислении площади под корнем получается отрицательное число.
=р*(р-a)*(р-b)*(р-с_) в ячейке В7 и определить его знак.
Если же нет, то в ячейке В8 вывести текстовую строку "Это не треугольник!", а в ячейках В10 и В11 вывести пустые строки. Результирующая таблица:
Аналогично можно скрывать и показывать столбцы.
Чтобы предохранить таблицу от непреднамеренной порчи неопытным пользователем, нужно защитить рабочий лист. Но сначала нужно "объявить беззащитными" ячейки с исходными данными.
Например, определить величину а при R = 3.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 елкнуть мышкой в окне ввода имени -
елкнуть мышкой в окне ввода имени - 
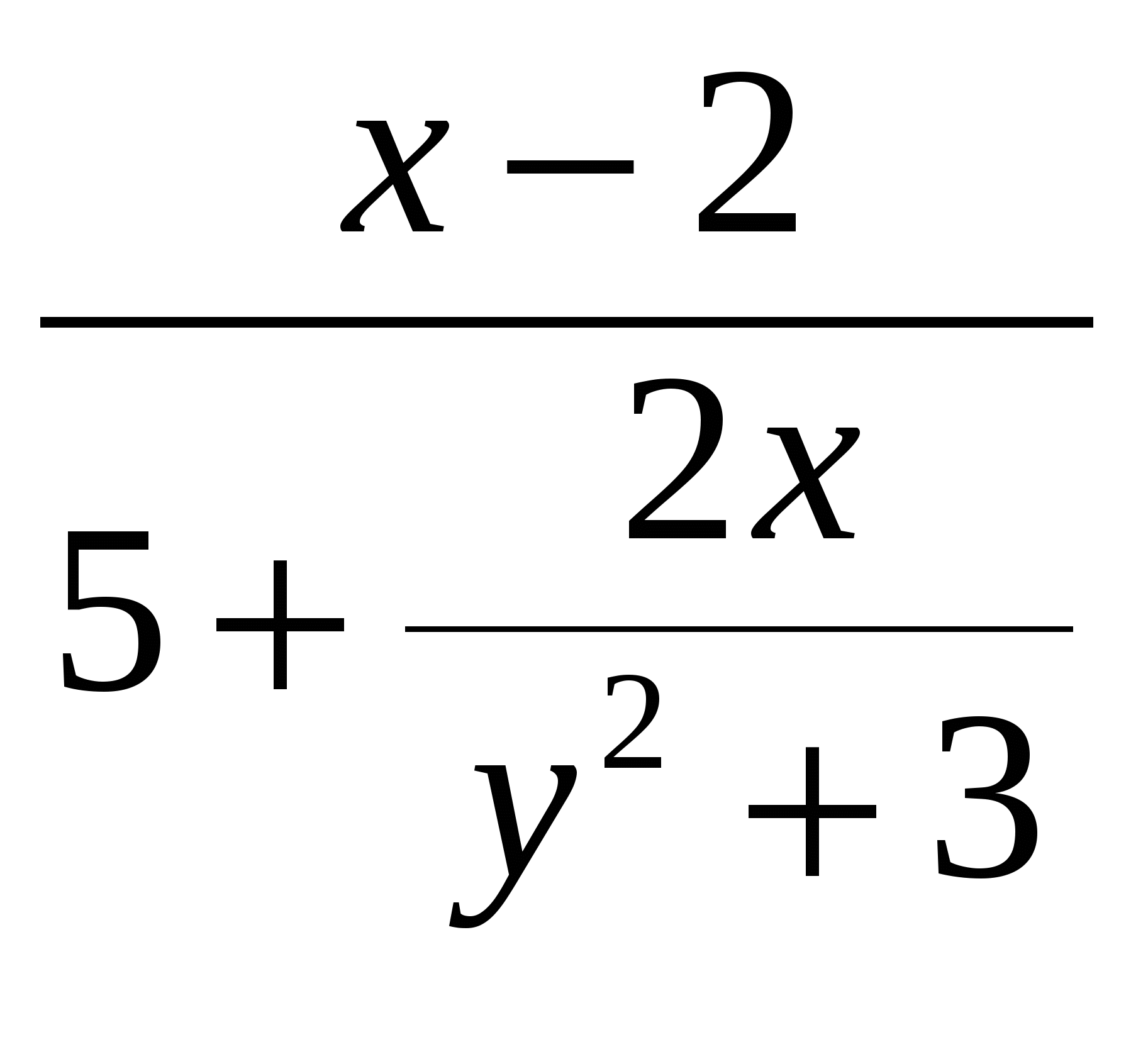 .
.  спользовать копирование формул.
спользовать копирование формул. азместить в В1 формулу =ОКРУГЛ(А1,2).
азместить в В1 формулу =ОКРУГЛ(А1,2).  х НЕ(х)
х НЕ(х)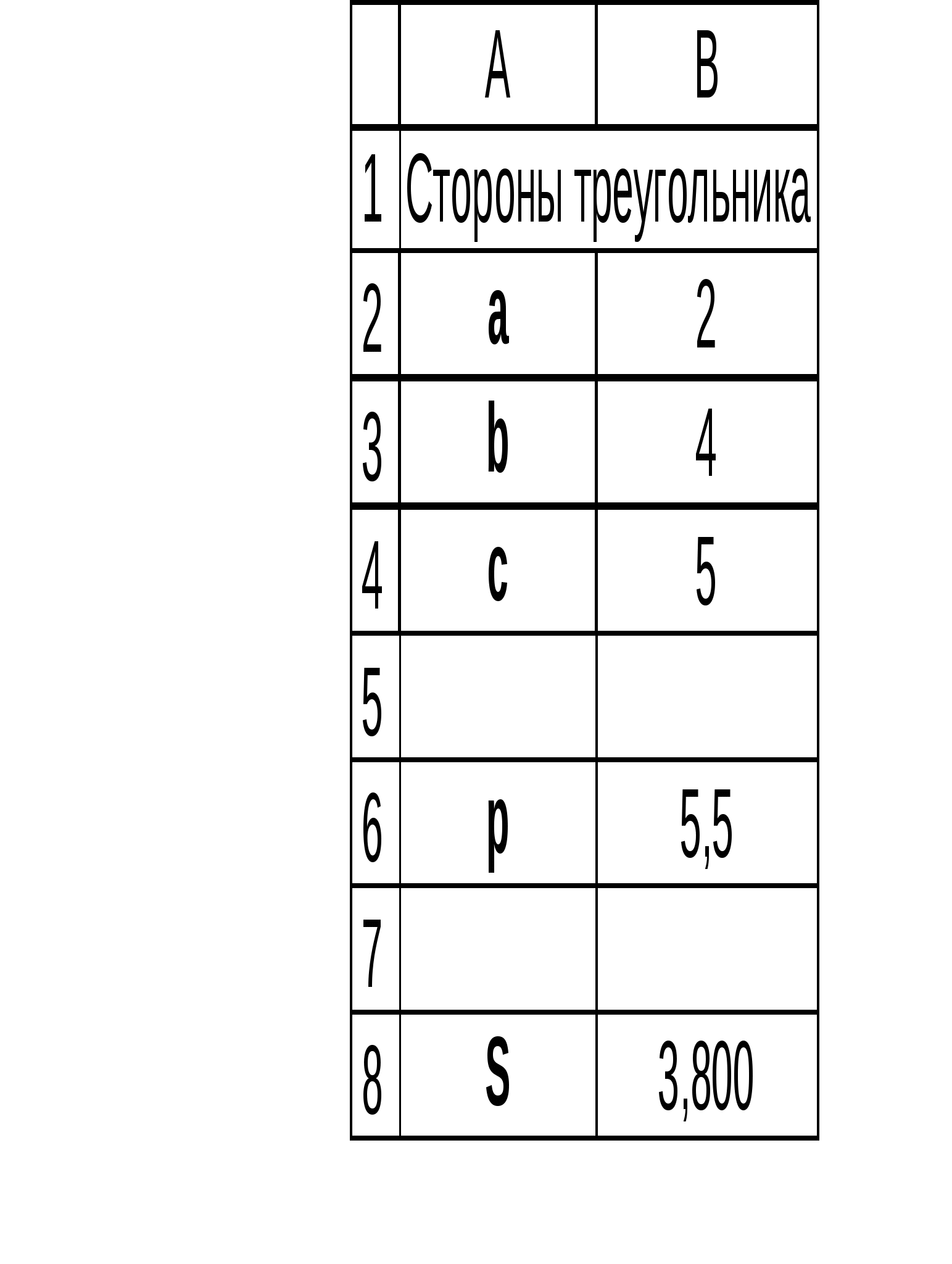 ячейку В6 ввести формулу =(В2+ВЗ+В4)/2.
ячейку В6 ввести формулу =(В2+ВЗ+В4)/2.