|
|
1_Вычисления в Excel. Учебное пособие Набережные Челны 2003 г
7 .2. Сложные проценты .2. Сложные проценты
В договорах указываются годовая ставка r и количество начислений процентов m в течение года. Это означает, что базовый период составляет год, деленный на m, а ставка сложных процентов для периода равна r/m. Формула для сложных процентов приобретает вид:
S + P ( 1 + 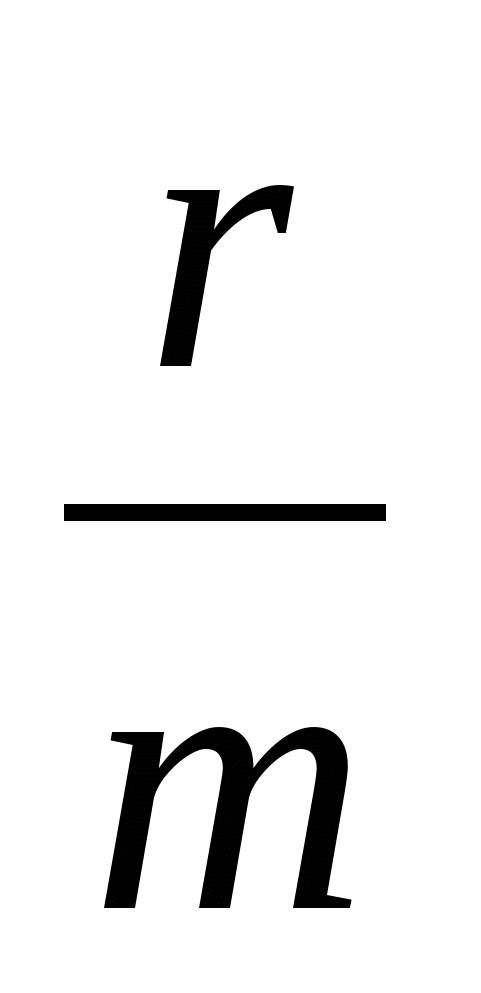 )T = 0 (Т измеряется в периодах). )T = 0 (Т измеряется в периодах).
Если начисление происходит k лет, то формула приобретает вид: S + P (1 + 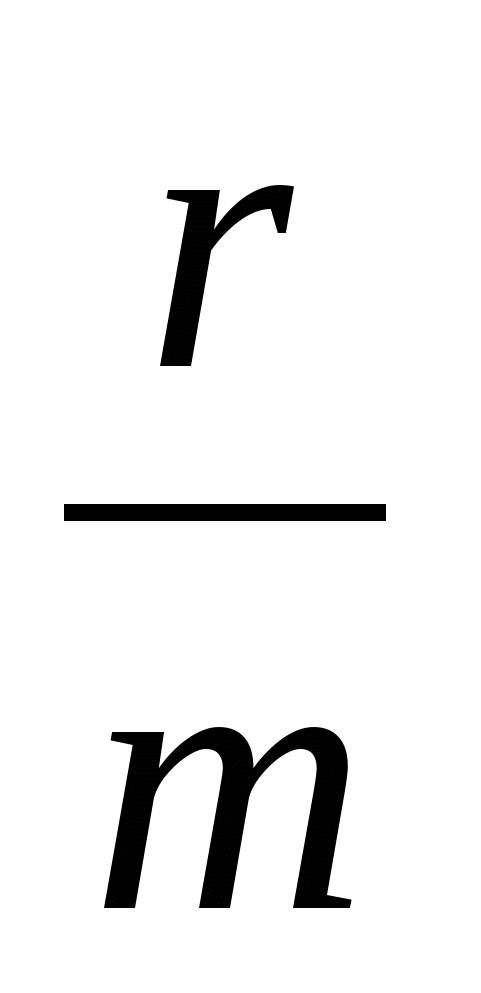 )km = 0. )km = 0.
Упражнение 7.2.1. Ссуда в 20 000 долл. дана на полтора года под ставку 28% годовых с ежеквартальным начислением. Определить сумму конечного платежа.
Решение. Здесь базовый период — квартал. Срок ссуды составляет 6 периодов (4 квартала в году, срок полтора года), за период начисляется 7% = 28%/4. Тогда формула, дающая решение задачи, имеет вид: = Б3 (28%/4, 4 * 1.5,, 20000).
Она возвращает результат: -30 014.61$.
Упражнение 7.2.2. По вкладу размером 2000 тыс. руб начисляется 10% годовых. Рассчитать, какая сумма будет на сберегательном счете через 5 лет, если проценты начисляются ежемесячно.
Решение: БЗ(10%/12;5*12;;-2000) Ответ - 3 290.62 тыс.руб.
Упражнение 7.2.3. На сберегательный счет вносятся платежи по 200 тыс.руб в начале каждого месяца. Рассчитать, какая сумма окажется на счете через 4 года при ставке процента 13,5 годовых.
Решение: =БЗ(13,5%/12;4*12;-200;;1)
Ответ - 12 779,34 т.руб.
Сравнить будущее значение счета, если платежи вносятся в конце каждого месяца.
Решение: =БЗ(13,5%/12;4*12;-200) Ответ - 12 637,17 тыс.руб.
Упражнение 7.2.4. Банк принимает вклад на срок 3 месяца с объявленной годовой ставкой 10% или на 6 месяцев под 11%. Как выгоднее вкладывать деньги на полгода: дважды на три месяца или один раз на 6 месяцев?
Решение: Вычислить коэффициенты наращения для обеих предлагаемых схем.
Для 1-ой схемы = Б3(10% * (3/12), 2,,-1000р.) =1 050,63р.,
для 2-ой схемы = Б3(11% * (6/12), 1,,-1000р.) =1 055,00р.
Упражнение 7.2.5. Рассчитать будущее значение вклада 1000 руб. через 0, 1, 2, 3, 4, 5 лет при годовых процентных ставках 10%, 20%,..., 50%.
Дополнительные поступления и выплаты отсутствуют.
Решение.
В ячейку В1 поместить величину начального значения вклада;
в ячейки B2:G2 разместить числа 0, 1,..., 5 - срок вклада;
в ячейки АЗ:А7 величины 10%, 20%,..., 50% - процентные ставки;
протабулировать функцию двух переменных (процентная ставка и количество лет), зависящую от параметра — начального вклада:
ввести в ячейку ВЗ формулу =БЗ( $АЗ; В$2;; -$В$1)
скопировать формулу в остальные ячейки интервала B3:G7.
и
зменяя значение в ячейке В1 рассчитать будущую сумму вклада.
Рис. 20. Таблица расчётов упражнения 7.2.5.
Если процентная ставка меняется с течением времени, то для расчёта будущего значения инвестиции (единой суммы) после начисления сложных процентов можно использовать функцию БЗРАСПИС (в англ. варианте - FvSchedule). Синтаксис функции:
БЗРАСПИС (инвестиция, {ставка1; ставка2; …; ставкаN})
Примечания.
Ставки необходимо вводить не в виде процентов, а как числа (0,1; 0,15; 0,05).
Вместо массива ставок можно указывать блок ячеек, содержащий процентные ставки.
Упражнение 7.2.6. По облигации номиналом 100 тыс.руб., выпущенной на 6 лет, предусмотрен следующий порядок начисления процентов: в 1-й год -10%, в два последующих года - 20%, в оставшиеся 3 года - 25%.
Рассчитать будущую стоимость облигации по сложной процентной ставке.
Решение: БЗРАСПИС (100, А1:А6) Результат= 309,38
(А1:А6 - 10%, 20%, 20%, 25%, 25%, 25%).
Задача 7.2.1. Построить семейство графиков зависимости будущего значения от срока (Упр.7.2.5).
Ф
орматировать шкалу значений как логарифми-ческую
и объяснить вид полученных графиков (рис. 21).
РРис. 21. Семейство графиков к задаче 7.2.1.
Задача 7.2.2. Рассчитать будущую стоимость облигации номиналом $300, выпущенной на 5 лет, если порядок начисления процентов таков: в первые два года -13,5% годовых, в следующие два года - 15%, в последний год - 20%.
|
|
|
 Скачать 7.26 Mb.
Скачать 7.26 Mb.