Математика и информатика. Учебное пособие по всему курсу Тольятти 2008 удк 51 004 (075. 8) Ббк 22. 1832. 81 Е егорова, Э. В. Учебное пособие по дисциплине Математика и информатика для студентов гуманитарных и педагогических специальностей очной формы обучения

• Название: Учебное пособие по всему курсу Тольятти 2008 удк 51 004 (075. 8) Ббк 22. 1832. 81 Е егорова, Э. В. Учебное пособие по дисциплине Математика и информатика для студентов гуманитарных и педагогических специальностей очной формы обучения
• Дата: 27.10.2020
• Размер: 1.82 Mb.
• Имя файла: Математика и информатика.doc
• Тип: Учебное пособие; #146041
• страница: 3 из 12

Глава 2. Основные понятия теории множеств. Основные структуры

В конце XIX века в математической науке возникла необходимость уточнить смысл таких понятий, как число, функция, непрерывность и т. д. Для этого нужно было определить, что такое натуральное число. Поиски ответа на эти сложные вопросы способствовали развитию новых математических идей. Поэтому в конце XIX и начале ХХ века происходил пересмотр старых представлений буквально во всех областях математических знаний. В результате в конце XIX века возникла новая область математики – теория множеств, одним из создателей которой был немецкий математик Георг Кантор [1845-1918]. За небольшой срок теория множеств стала фундаментом всей математики. В теории множеств в полной мере используется аксиоматический подход, то есть используются постулаты, утверждения без доказательств. В частности, аксиомы, определяющие множество N – натуральных чисел, множество Z – целых чисел, аксиомы умножения, полной упорядоченности. Ввиду очевидности каждого из постулатов, данные аксиомы в дальнейшем изложении опускаются.

Современная математика занимается не столько объектами исследования, сколько структурой отношений между этими объектами. Математика в первую очередь уделяет внимание основным структурам, в частности, таким понятиям: число, точка, векторные пространства, числовые функции, пределы и так далее, которые составляют в целом элементарную математику.

Основные структуры являются началом для построения всех разделов математики. Теория множеств занимается структурой отношений между этими объектами. В ней уточняется смысл основных терминов обиходного языка, вводятся символы, устанавливающие условия существования отношений, позволяющие выразить сжато, с помощью формул высказывания, которые лучше выявят их логическое и математическое содержание. На основе теории множеств появился теоретико-множественный язык, который позволяет описывать и объяснять математические высказывания в краткой и понятной форме, используя специальные символы и термины. Этот язык применяется во всех разделах математики. Каждый обучающийся математике независимо от специализации должен знать и понимать этот язык, как фундамент, на котором строятся основные понятия, методы в последующих разделах и курсах, которые требуется изучить.

2.1. Понятие множества

Главные математические понятия: точка, прямая, множество, функция, вектор, уравнение, отношение и т.д. образуют основания математики. В каждом разделе математики используется какое-то понятие из оснований математики. Понятия: натуральные числа, целые или вещественные числа, геометрические фигуры, числовые функции и т.д. называют множествами. Понятие множества является фундаментальным понятием математики. Если обратиться к первой главе, то можно это понятие по правилам аксиоматического построения теории отнести к первичным, для которых нет определений. Обычно слово «множество» связывают с большим числом предметов. Например: множество дорог, машин, газет, учащихся школ, студентов вузов. В отличие от обыденных представлений «множество» как производное от слова «много», в математике можно рассматривать множество, состоящее из одного объекта или не содержащее ни одного объекта.

В 1872 г. Георг Кантор, создатель теории множеств, определил множество как «объединение в одно целое объектов, хорошо различимых нашей интуицией или нашей мыслью». Понятие множества аналогично определениям совокупности, собрания, класса, семейства и т.д. Математическое понятие множества постепенно выделилось из выше перечисленных представлений. Понятие числа относится к так называемым начальным понятиям, т.е. к понятиям, которые могут быть разъяснены, но не могут быть строго определены. Для числовых множеств в математике приняты стандартные обозначения:

N – множество натуральных чисел;

Z – множество целых чисел;

Q – множество рациональных чисел (дробь m/n,где m,n – целые числа);

R – множество вещественных (действительных чисел) чисел;

R+ – множество вещественных положительных чисел;

C – множество комплексных чисел.

Таким образом, можно сделать вывод:

Понятие «множество» является фундаментальным понятием математики и не имеет определения. Природа порождения любого множества разнообразна, в частности, окружающие предметы, живая природа и др.

Определение 1: Объекты, из которых образовано множество, называются элементами данного множества. Для обозначения множества используют заглавные буквы латинского алфавита: например X, Y, Z, а в фигурных скобках через запятую выписывают его элементы строчными буквами, например: {x,y,z}.

Пример обозначения множества и его элементов:

X = {x₁, x₂,…, x_n} – множество, состоящее из n элементов. Если элемент x принадлежит множеству X, то следует записать: xX, иначе элемент x не принадлежит множеству X, что записывается: xX. Элементами абстрактного множества могут быть, например, числа, функции, буквы, фигуры и т.д. В математике в любом разделе используется понятие множества. В частности, можно привести некоторые конкретные множества вещественных чисел. Множество вещественных чисел х, удовлетворяющих неравенствам:

• 
  а ≤ x ≤ b называется сегментом и обозначается [a,b];
  
• 
  а ≤ x < b или а < x ≤ b называется полусегментом и обозначается: [a,b) или (a,b];
  
• 
  а < x < b называется интервалом и обозначается (a,b).
  

Определение 2: Множество, имеющее конечное число элементов, называется конечным. Пример. X = {x₁, x₂, x₃}.

Определение 3: Множество называется бесконечным, если оно состоит из бесконечного числа элементов. Например, множество всех вещественных чисел бесконечно. Пример записи. X = {x₁, x₂, ...}.

Определение 4: Множество, в котором нет ни одного элемента, называют пустым множеством и обозначают символом .

Характеристикой множества является понятие мощности. Мощность – это количество его элементов. Множество Y={y₁, y₂,...} имеет ту же мощность, что и множество X={x₁, x₂,...}, если существует взаимно однозначное соответствие y= f(x) между элементами этих множеств. Такие множества имеют одинаковую мощность или равномощны. Пустое множество имеет нулевую мощность.

2.2. Способы задания множеств

Можно отметить два способа задания множеств:

1. 
   Задать полный перечень элементов этого множества. Первый способ задания множества называется перечислением. Пример. F={3,5,7,9}.
   
2. 
   Указать Р – свойство или правило для определения того, принадлежит или нет рассматриваемому множеству данный объект. В этом случае указывается характеристическое свойство элементов множества.
   

Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит. С его помощью можно описывать какие угодно множества в удобном и компактном виде.

Запись в виде {x  X: P(x)} или {x  X | P(x)} обозначает множество элементов х, обладающих свойством Р. Запись Х={x | P(x)} означает, что элемент х принадлежит множеству Х (х  Х) тогда и только тогда, когда P(x) истинное утверждение.

Пример 1. Запись Х={x | x  N: x < 9} означает, что х  Х тогда и только тогда, когда х – натуральное число и меньше 9.

Пример 2. Учитывая, что N – множество натуральных чисел, то запись:

{x  N: x²–25=0} означает множество корней уравнения x²–25=0, являющихся натуральными числами. В данном случае это множество состоит из одного элемента {5}. В этих примерах вначале указывается элемент множества, далее характеристика порождения элемента. Для бесконечных множеств предпочтительнее второй способ описания. Примеры записи:

1) Z={z | z – нечётные числа};

2) S={s | s = x_i² + y_i², где: x_i, y_i – координаты точки, i =1,2,...}.

2.3. Алгебра множеств

Первоначально алгеброй называли учение о решении уравнений. За много столетий своего развития алгебра превратилась в науку, которая изучает операции и отношения на различных множествах. Математика рассматривает не только объекты, но и главным образом связи между ними. Современная алгебра рассматривает общие понятия: понятия соответствия, отношения, алгебраических операций и другие.

2.3.1. Отношения между множествами

В математике часто используется для обозначения какой-либо связи между предметами или понятиями термин «отношение». Примеры отношений: отношение равенства между двумя или несколькими переменными, фигурами. В математике изучают не только те или иные множества, но и отношения, взаимосвязи между ними.

Определение 5: Множество В является подмножеством множества А, если каждый элемент множества В является также элементом множества А. Утверждение, что множество В является подмножеством множества А, записывают так: ВА. Такая запись означает, что каждый элемент множества В является элементом множества А и множество В включено во множество А.

Пример 3. Пусть В {2, 4, 6} – множество чётных чисел, А{1, 2, 3, 4, 5, 6, 7} – множество целых чисел. Следовательно, множество В включено во множество А, что записывается так: ВА, но множество А не включено во множество В, что записывается так: А  В. Например, множества {4, 8} и {6} являются подмножествами множества {2, 4, 6, 8}; а числа 2, 4, 6, 8 – его элементы.

Свойства включения множеств:

1. 
   Пустое множество является подмножеством любого множества:   А.
   
2. 
   Любое множество является подмножеством самого себя, т.е. для любого множества А справедливо включение А  А.
   

Определение 6: Два множества равны, если каждое из них является подмножеством другого (A = B  (A  B и В  А)). Множества, состоящие из одних и тех же элементов, называются равными. При этом порядок перечисления элементов множества значения не имеет. Например. Равны множества {8,2,5}, {2,5,8} и {5,8,2}.

Если множество X равно множеству Y, то можно записать X = Y. В противном случае X ≠ Y. Другой пример. Даны множества: Z ={3,5,7}, Y = {7,5,3,5,7}. Они равны Z=Y, так как они состоят из одних и тех же элементов. Множество Z={3,5,7}, X={{7,5}, {3,5,7}} не равны Z≠X, так как элементами второго множества являются множества. Таким образом, данные множества состоят из элементов различной природы и не могут быть равны.

Считается, что пустое множество является подмножеством любого множества. У любого множества есть обязательно хотя бы два подмножества: пустое множество и само множество. Эти два подмножества называются несобственными подмножествами. Любое подмножество, отличное от несобственного, называется собственным подмножеством данного множества.

У пустого множества нет собственных подмножеств, а оба несобственных подмножества равны между собой. У любого одноэлементного множества также нет собственных подмножеств, но его несобственные подмножества различны. У любого двухэлементного множества есть уже два собственных подмножества. С ростом количества элементов во множестве количество собственных подмножеств растет. Например, если F={3,5}, то собственными подмножествами множества F будут являться множества {3} и {5}.

Определение 7: Множество всех подмножеств множества А называется множеством-степенью множества А и обозначается через R(A).

Пусть А={5,3,9}. Тогда множество-степень состоит из:

1) А={5,3,9} – исходного множества.

2) пустого множества .

3) трёх одноэлементных подмножеств: {5}; {3}; {9}.

4) трех двухэлементных подмножеств множества А: {{5,3}{3,9}{5,9}}.

Таким образом, множество-степень:

R(A) = {А,{5},{3},{9},{5,3},{3,9},{5,9},{}}; состоит из 2³=8 элементов.

Для n-элементного множества множество-степень состоит из 2ⁿ элементов.

2.3.2. Операции над множествами

Известно, что над числами можно производить следующие элементарные операции: сложение, умножение, вычитание. Над множествами вводятся аналогичные операции.

Определение 8: Объединением двух множеств называется третье множество С, состоящее из элементов, принадлежащих хотя бы одному из множеств А или В. Объединение множеств А и В обозначается:

AB = {x xA или xB}.

Пример 4. Пусть А = {1, 2, 3}, В = {3, 4, 5}. Тогда АВ = {1,2,3,4,5}. Таким образом, если элемент x принадлежит объединению АВ, то он может принадлежать или множеству А, или множеству В, или обоим этим множествам. Можно сформулировать иначе: x  АВ тогда и только тогда, когда х есть элемент хотя бы одного из этих множеств. В последнем примере числа 1, 2 принадлежат множеству А. Числа 4, 5 принадлежат множеству В, число 3 принадлежит обоим множествам сразу. Графически объединение множеств А и В можно представить на рис. 2.1.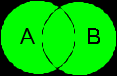



Рис. 2.1. Объединение множеств А и В

Определение 9: Пересечение множеств А и В есть множество, состоящее из элементов, общих для обоих множеств. Пересечение множеств обозначается: AB = {x xA и xB}.

Пример 5.

Пусть даны множества: А = {1, 2, 3}, В = {3, 4, 5}. Тогда: АВ = {3}.

В результате можно сделать вывод, что:

• 
  Пересечение множеств А и В включено во множество А, что записывается: ABA.
  
• 
  Пересечение множеств А и В включено во множество В, что записывается: ABB.
  
• 
  Пересечение множеств А и В включено в объединение множеств, что записывается:ABAB.
  

Может оказаться, что множества не имеют ни одного общего элемента. В этом случае множества не пересекаются и их пересечение – пустое множество.

Пример 6. Пусть А = {7,9,5}, В = {2, 4,6}. Тогда АВ =.

Пересечение множеств А и В графически можно представить на рис. 2.2 (затенённая область).



Рис. 2.2. Пересечение множеств А и В

Свойства пересечения множеств:

1. A=.

2. AA=A.

3. AB=BA.

4. A(BC)=(AB)C=ABC.

5. ABAB=A.

Определение 10: Разностью двух множеств А и В называется новое множество, все элементы которого являются элементами множества А, но не являются элементами множества В. Обозначается:

A\B = {x xA ; xB}.

Пример 7. Пусть А = {1, 2, 3, 4}; В = {3, 4, 5, 6}.

Тогда А\В = {1, 2}; В\А= {5, 6}.

Разность множеств А и В графически можно представить на рис. 2.3 (затенённая область):



Рис. 2.3. Разность множеств А\В

Если рассматриваемое множество В является подмножеством некоторого фиксированного множества А, то разность А\В называется дополнением множества В или дополнением до А множества В.

Определение 11: Разбиением множества Х называется такая расчленённая система Y непустых подмножеств множества Х, что каждый элемент множества Х является элементом некоторого множества системы Y.

Пример 8. Множество Y={{7,5}, {3,4}, {9,6}, {17,8}} есть результат операции разбиения множества X = {7, 5, 3, 4, 9, 6, 17, 8}. Данная операция позволяет образовать новое множество Y из одного существующего множества X. Можно выделить такое множество, что все рассматриваемые предметы являются его элементами. Такое множество называется универсальным. Обычно универсальное множество обозначается через U.

Дополнением множества А называется множествоА, состоящее из элементов множества U, не являющихся элементами множества А:

А ={x | xU;xA}.

На диаграммах универсальное множество обозначают в виде прямоугольника и буквы U, а множества, входящие в универсальное множество, – в виде кругов внутри прямоугольника (рис. 2.4).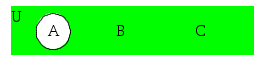



Рис. 2.4. Универсальное множество U

Разность между универсальным множеством U и множеством А называется дополнением множества А.

Обозначается:A=U\A (затенённая область рис. 2.5).



Рис. 2.5. Разность U\A

2.3.3. Алгебраические свойства операций над множествами

После изучения операций над множествами следует рассмотреть свойства этих операций и связи между ними. Эти свойства во многом аналогичны свойствам обычных операций сложения и умножения чисел. Свойства записываются в виде тождеств и не зависят от того, каково универсальное множество U и какие именно конкретные его подмножества в них фигурируют. Далее формулируются основные свойства объединения и пересечения.

Для любых подмножеств А, В, С универсального множества U справедливы следующие тождества, которые приведены в таблице 2.1.

Таблица 2.1

1	Коммутативность
для объединения		для пересечения
1a	A  B = B  A	1b	A  B = B  A
2	Ассоциативность
2а	A  (B  C) = (A  B)  C	2b	A  (B  C) = (A  B)  C
3	Дистрибутивность
3а	A(BC) = (AB)  (AC)	3b	A (BC) = (AB)(AC)
4	Операции с пустым и универсальным множествами
4а	A   = A	4b	A  U = A
5а	A  = U	5b	A  = 

Каждое из этих тождеств можно доказать, показав, что множество, стоящее по одну сторону тождества включено во множество, стоящее по другую сторону. Если:

1. 
   Операции объединения множеств  поставить в соответствие операцию сложения чисел.
   
2. 
   Операции пересечения  поставить в соответствие операцию умножения чисел.
   
3. 
   Универсальному множеству U поставить в соответствие единицу.
   
4. 
   Пустому множеству  поставить в соответствие нуль, то возникает аналогия между множествами и числами.
   

Закон коммутативности для множеств в табл. 2.1 аналогичен переместительному закону для чисел:

1a

a+b=b+а;

1b

a  b = b  а;

Закон ассоциативности для множеств в табл. 2.1 аналогичен сочетательному закону для чисел:

2a

a+(b+c)=(a+b)+c;

2b

a  (b  c) = (a  b)  c.

Закон дистрибутивности 3б) для множеств в табл. 2.1 аналогичен распределительному закону для чисел: a  (b+c) = a  b+a  c.

Закон дистрибутивности 3а) для множеств нарушается для чисел.

Десять свойств, сформулированных в этом разделе, являются фундаментальными в том смысле, что все остальные свойства операций над множествами непосредственно следуют из них.

2.3.4. Геометрическая интерпретация операций над множествами

Диаграммами Эйлера [1707-1783] (в США – диаграммами Венна) называют фигуры, изобржающие множества и наглядно демонстрирующие операции над множествами и некоторые свойства этих операций. С помощью диаграмм Эйлера удобно иллюстрировать операции над множествами. Все ранее приведённые рисунки являются геометрической интерпретацией операцией над множествами (рис. 2.12.5). Диаграммами Эйлера можно представить всю последовательность выполнения алгебры множеств.

2.4. Декартово произведение множеств. Бинарные отношения

Отношения между двумя и более множествами рассматриваются в разделе 2.3.1. Данная операция позволяет их сравнивать и делать вывод о равенстве или включении одного множества в другое. Известно, если два множества состоят из одних и тех же элементов, то эти множества равны независимо от порядка их следования. Однако в математике рассматриваются множества, где учитывается порядок следования элементов множества. В том случае, когда важен порядок следования элементов, в математике вводят понятие упорядоченных наборов элементов. Двухэлементное множество {x, y}, в котором элемент х стоит на первом месте, а y – на втором называется упорядоченной парой (x; y). Упорядоченную пару, образованную из элементов: х , y принято записывать в круглые скобки (x; y). Элемент x называют первой координатой пары, а элемент y – второй. Две пары равны, если их координаты совпадают. Если сравнить два множества: {2,5}; {5,2}, то можно отметить, что они равны, так как они состоят из одинаковых элементов. Если сравнить две упорядоченные пары: (2; 5), (5; 2), то следует отметить, что они не равны, так как их координаты не совпадают. В этом основное отличие упорядоченной пары от двухэлементного множества.

Упорядоченные пары можно образовывать как из элементов одного множества, так и двух множеств. В примере 9 рассматривается образование упорядоченных пар из элементов двух множеств.

Пример 9.

Пусть заданы два множества: X={7,5}, Y={1,4,8}. Из этих множеств можно создать новое множество, перечислив все упорядоченные пары:{(7;1), (7;4), (7;8), (5;1), (5;4), (5;8)}. В полученном множестве каждый элемент является упорядоченной парой, в которой первая компонента принадлежит множеству X, вторая множеству Y.

При создании нового множества элементы первого множества должны стоять на первом месте, элементы второго множества должны стоять на втором месте. Множество, элементами которого являются упорядоченные пары чисел, называется декартовым произведением. На примере 9 можно отметить: создание нового множества, состоящего из упорядоченных пар, аналогично перемножению элементов двух скобок, т.е. заданных множеств X,Y , только операция умножения заменяется построением соответствующих пар.

Определение 12: Декартовым произведением множеств X и Y называется множество всех пар (x, y), первая компонента которых xX, вторая компонента y  Y. Декартово произведение множеств X и Y обозначают X  Y и его можно записать: X  Y = {(x; y) | x  X ; y  Y }.

Аналогично можно конструировать новые множества, используя вместо пар (x,y) наборы из n –элементов {а, x, y,...}. Упорядоченные наборы, состоящие из n – элементов (n-ки) называют кортежами. Длина кортежа – это число элементов, из которых он состоит. Например, (с, т, у, д, е, н, т) – это кортеж длины 7. Тогда, декартово произведение n – множеств есть множество кортежей, построенных из n – элементов этих множеств.

В упорядоченных кортежах компоненты могут находиться в какой-то связи, т.е. отношении. Если рассматривают отношения между объектами, то это: «больше», «меньше», «равно». Например: x>y; z
Из этих примеров видно, что отношение используется для двух объектов, записанных в определенном порядке. Если две упорядоченные пары равны, то они находятся в отношении равенства. Чтобы определить отношение, достаточно перечислить все пары, которые находятся в данном отношении.

Отношение –  из X в Y есть некоторое множество упорядоченных пар (x; y), где: x  X, y  Y. Так как отношение связывает два объекта, его назывют бинарным. Если (x, y)  , где  есть некоторое множество упорядоченных пар, то элемент х находится в отношении  с элементом y.

Если рассматривают отношения между тремя элементами, то их называют тернарными, отношения между n элементами – n-арными. Примером тернарного отношения может служить отношение между точками прямой: точка х лежит между двумя точками прямой (z, y). Если рассматривать некоторую точку, удовлетворяющую или нет данному отношению (например, принадлежности прямой), то данное отношение будет унарным. В математике чаще всего встречаются бинарные отношения – множество пар, т.е. отношения, заданные на декартовом произведении двух множеств: А1А2.

Примеры бинарных отношений:

• 
  Бинарное отношение старшинства между двумя людьми по возрасту или воинскому званию.
  
• 
  Бинарное отношение между целыми числами – «иметь одинаковые остатки от деления на 7».
  

Можно отметить виды отношений между элементами множества.

1. 
   Отношения эквивалентности. В этом случае выделяется какое-то свойство множества (например, положительные или отрицательные числа, чёрный или белый цвет). По этому свойству элементы, принадлежащие одному классу эквивалентности, являются эквивалентными. Например. Отношение параллельности на множестве прямых. Отношение подобия на множестве всех треугольников на плоскости.
   
2. 
   Отношения частичного порядка. Примеры отношений частичного порядка: числа кратные двум, или трём, или семи и т. д., отношения «больше» или «меньше», x > y, z < r. Пример. Отношение на множестве задано неравенством: 5x-2y>0. Можно построить новое множество, которое соответствует данному отношению: {(1,0);(2,1);(3,2)}. Данное множество состоит из упорядоченных пар, каждая из которых удовлетворяет заданному отношению.
   
3. 
   Отношения строгого порядка (зависимости). Примеры отношений зависимости: табличная, функциональная y=f(x). График функции есть множество упорядоченных пар: G = {(x, y) | x  X; y  f(x)}.
   

Рассмотрим различные виды бинарных отношений на примерах. Множество {(2;4), (7;3), (3;3), (2;1)} есть множество упорядоченных пар. Однако между парами отсутствует связь. Если установить отношение «меньше»: x < y , то множество можно записать для примера в виде: {(2;3), (4;7), (5;8), (8;17)}. В последнем примере элементы множества располагаются по возрастанию. Такое отношение называется отношением частичного порядка, а множество из таких элементов получится частично упорядоченным.

Иначе можно записать бинарные отношения, если между ними установить функциональную зависимость.

Пример 10.

y=x+2, множество из порядоченных пар можно записать в виде:

{(2;4), (4;6), (6;8), (8;10)}. В общем виде: {(x, y) | x  X; y = x+2}.

Пример 11.

Пусть задано отношение на множестве в виде функциональной зависимости. Z = {(x, y) | x  X; y = x²}. В этом примере можно строить любое множество из упорядоченных пар, задаваясь значением х и вычисляя y = x². Например. {(1,1);(2,4);(3,9)(4,16)}.

Пример 12.

D={(x; y)| x  X; y = cos x}. Если построить график данной зависимости на координатной плоскости, то он будет наглядным представлением отношения. В данном случае каждая упорядоченная пара отношения (x, y)   графически может быть представлена точкой на плоскости. Соединив все точки данной функциональной зависимости кривой линией, можно получить графическое представление бинарного отношения.

Обобщая выше рассмотренное, можно отметить:

1. 
   Бинарное отношение из множества X в множество Y есть подмножество декартова произведения множеств:   X  Y. Отношения состоят из однотипных кортежей.
   
2. 
   Бинарное отношение на множестве Х есть всякое подмножество декартова произведения   Х  Х.
   

Пример 13.

Пусть на множестве Х={3, 5, 7} задано отношение «меньше» (т.е. первый элемент меньше второго, второй меньше третьего). Записать декартово произведение X  Х.

Решение.

Декартово произведение X  Х может быть записано в виде множества из упорядоченных пар: {(3,3);(3,5);(3,7);(5,3);(5,5);(5,7);(7,3);(7,5);(7,7)}. Из этого множества следует выбрать элементы, которые должны удовлетворять отношению «меньше». В результате получится новое множество из упорядоченных пар: {(3;5), (3;7), (5;7)}. В новом множестве все пары являются элементами декартова произведения Х  Х. Отношение «меньше» на множестве Х является подмножеством декартова произведения Х  Х.

3. Подмножество R декартова произведения множеств Х₁Х₂Х₃ ... X_n называется отношением степени n (n-арным отношением).

В математике, как правило, отношения заданы на бесконечных множествах и имеют бесконечную мощность. Отношение – понятие очень широкое. Поскольку отношения являются множествами, то к ним применимы все теоретико-множественные операции: объединение, пересечение, дополнение и др.

2.5. Символический язык логической структуры математических предложений

Математика описывает исследуемые процессы, используя кроме словесного языка символический. Каждое математическое предложение характеризуется содержанием и логической формой, причем они взаимосвязаны.

При записи математических предложений используются обозначения логики:

1. 
   Логические символы:
   

a)  логический вывод (дедукция), который означает: «влечет за собой».

b)  логическая равносильность, которая означает: «эквивалентно».

2. 
   Кванторы:
   

a)  квантор существования.

«x» означает: «существует по меньшей мере один х такой, что …».

Запись: «x:А(х)»; означает: «существует такое значение х, что А(х) – истинное высказывание».

b) – квантор общности, который означает «любой» или «для всех».

Основным объектом математической логики является высказывание.

Определение 13: Высказыванием в математике называют предложение, относительного которого имеет смысл вопрос истинности или ложности его.

В логике считают, что из двух данных предложений можно образовать новые предложения, используя для этого слова: «и, или, если…, то», которые называют логическими связками. Предложения, образованные из других предложений с помощью логических связок, называют составными. Выделяют пять основных логических связок, которые позволяют получить новые высказывания:

1. Отрицание – это высказывание, которое получается из данного высказывания А с помощью слова «не». Отрицание обозначаетсяА.

2. Конъюнкция высказываний А и В – это высказывание АB, которое истинно, когда оба высказывания истинны, и высказывание АB ложно, когда хотя бы одно из этих высказываний ложно. Конъюнкция получается из двух данных высказываний А и В с помощью союза «и».

Пример 14. Пусть высказывание А: «студент сдал экзамен по истории», высказывание В: «сдал экзамен по иностранному языку».

Конъюнкция высказываний А и В (АB): «студент сдал экзамен по истории и сдал экзамен по иностранному языку».

3. Дизъюнкция высказываний А или В – это высказывание АB, которое истинно, когда истинно хотя бы одно из этих высказываний, и высказывание АB ложно, когда оба высказывания ложны. Дизъюнкция получается из двух данных высказываний А, В с помощью союза «или».

Пример 15. Пусть высказывание А: «студент сдаёт экзамены на хорошо», высказывание В: «сдаёт экзамены на отлично».

Дизъюнкция высказываний А или В (АB): «студент сдаёт экзамены на хорошо или сдаёт экзамены на отлично».

4. Импликация образуется из двух данных высказываний А и В с помощью слов «если…, то…».

Импликация обозначается AB (если А, то В).

Пример 16. Если студент сдаёт сессию без троек и двоек, то он получает стипендию. Здесь высказывания: А – «студент сдаёт сессию без троек и двоек», В – «он получает стипендию».

5. Эквиваленция образуется из двух данных высказываний А и В с помощью слов «тогда и только тогда, когда…».

Эквиваленция обозначается: AB.

Пример 17. «Студент получает стипендию тогда и только тогда, когда он сдаёт экзамены на хорошо или отлично». Здесь высказывания: А – «студент получает стипендию», В – «он сдаёт экзамены на хорошо или отлично».

Для примера рассмотрим несколько высказываний с применением кванторов.

Пример 18. Если В есть подмножество Х и элемент х принадлежит В, то это можно записать в виде: x:xBxX. Эту строку можно прочитать так: для любого х, если х принадлежит подмножеству В, то это влечет за собой (следует) утверждение, что х принадлежит множеству Х.

Пример19. Запись: a:[aAB][aAaB] можно прочитать: для любого элемента а, если а принадлежит пересечению множеств А и В, то это равносильно, что а принадлежит множеству А и множеству В.

Пример 20. Запись: x:xAB означает: существует по меньшей мере один х такой, что элемент x принадлежит пересечению множеств А и В.

Пример 21. Запись «z:[zZ]xX:x=cos(z)», можно прочитать: для любого элемента z, если z принадлежит множеству Z, то из этого следует, что существует по меньшей мере один х, принадлежащий множеству Х такой, что элемент x равен cos(z).

2.6. Алгебраические операции над различными математическими объектами

В математике изучают не только отношения, но и различные операции над различными математическими объектами. В качестве математических объектов можно перечислить: числа, множества, высказывания.

Для чисел: умножение, деление сложение, вычитание. Для множеств: пересечение, объединение, вычитание. Над высказываниями: конъюнкция, дизъюнкция, отрицание. Операции над высказываниями и множествами появились в математике в XIX веке, и ввел их английский математик Дж. Буль [1815-1864] (булева алгебра). Операции над множествами ввел немецкий математик Г. Кантор. Оказалось, что операции над множествами и высказываниями обладают свойствами, аналогичными свойствам сложения и умножения чисел, но некоторые отличаются от свойств операций над числами. В XIX веке в математике возникли разные ветви алгебры: обычных чисел, множеств, высказываний и другие.

Появилось общее понятие алгебраической операции. В математике вводятся понятия операций над элементами множества произвольной природы и изучаются свойства таких операций. Основная идея состоит в том, чтобы изучать не свойства конкретных элементов конкретных множеств, а свойства операций над этими элементами. Множества вместе с определенными на них операциями образуют алгебру множеств. Последовательность выполнения операций задаётся с помощью формулы алгебры множеств.

Например, A(ВC), (X\Y)  Z – формулы алгебры множеств.

Пример 22.

Дано три множества М = {7, 2, 3, 5}, N = {1, 2, 4, 7, 9},

K = {6, 7, 9}.

Найти:

X=(MN)(MK)\(NК)(N\K).

Z=(NM)(MK)\(KN)(N\K).

Решение.

1) MN= {7, 2};

2) MК = {7};

3) NК={7, 9};

4) MK={2, 3, 5, 6, 7, 9};

5) NМ= {1, 2, 3, 4, 5, 7, 9};

6) KN={1, 2, 4, 6, 7, 9};

7) N\K={1, 2, 4}.

X=(MN)(MK)\(NК)(N\K)={1, 2, 4}.

Z=(NM)(MK)\(KN)(N\K)={1, 2, 3, 4,5}.

2.7. Вопросы для самоконтроля по теме «Теория множеств»

1. X={5,7,3} и Z={7,2,3,4,5}, тогда для них верным утверждением будет:

a) «Множества X и Z равны»;

b) «Множества X и Z не имеют общих элементов»;

c) «Множество X включает в себя множество Z»;

d) «Множество X есть подмножество множества Z».

2. Заданы множества M={9,3,1,5} и N={9,1}, тогда для них верным утверждением будет:

a) «Множество M есть подмножество множества N»;

b) «Множества M и N не имеют общих элементов»;

c) «Множества M и N равны»;

d) «Множество M включает в себя множество N».

3. Заданы множества A={1,2,3} и M={0,2,3,6,1}, тогда для них верным утверждением будет:

a) «Множество А включает в себя множество М»;

b) «Множества A и M равны»;

c) «Множество А есть подмножество множества М»;

d) «Множество М есть подмножество множества А».

4. Заданы множества A={2,4,3,1} и B={4,2,1,3}, тогда для них неверным утверждением будет:

a) «Множества A и B равны»;

b) «Множества A и B не имеют общих элементов»;

c) «Множество A включает в себя множество B»;

d) «Множество A есть подмножество множества B».

5. Заданы множества C={7,2,5} и D={3,2,1}, тогда для них верным утверждением будет:

a) «Множество D является подмножеством множества C»;

b) «Множество C является подмножеством множества D»;

c) «Множества C и D равны»;

d) «Множество C не равно множеству D».

6. Заданы множества M={9,5,4} и N={9,1,4,2,5,3}, тогда для них верным утверждением будет:

a) «Множество M есть подмножество множества N»;

b) «Множества M и N не имеют общих элементов»;

c) «Множества M и N равны»;

d) «Множество M включает в себя множество N».

7. Если сравнить две упорядоченные пары: (3;9) и (9;3), то они находятся в отношении:

a) «функциональной зависимости»;

b) «не имеют общих элементов»;

c) «равенства».

d) «не равенства».

8. Заданы две упорядоченные пары: (8;1), (1;8) двух множеств: A={8,4,1} и B={1,4,8}, которые находятся в отношении:

a) «равенства».

b) «функциональной зависимости»;

c) «не равенства».

d) «упорядоченности по убыванию».

9. Отношение задано неравенством: x-3y>0, тогда данному отношению принадлежит следующая пара чисел:

a) (5; 2); b) (1; 1); c) (5; 1); d) (0; 0).

10. Отношение задано неравенством: 5x+y<0, тогда данному отношению принадлежит следующая пара чисел:

a) (1; 2); b) (-1; 1); c) (1; -1); d) (0; 0).