Математика и информатика. Учебное пособие по всему курсу Тольятти 2008 удк 51 004 (075. 8) Ббк 22. 1832. 81 Е егорова, Э. В. Учебное пособие по дисциплине Математика и информатика для студентов гуманитарных и педагогических специальностей очной формы обучения

• Название: Учебное пособие по всему курсу Тольятти 2008 удк 51 004 (075. 8) Ббк 22. 1832. 81 Е егорова, Э. В. Учебное пособие по дисциплине Математика и информатика для студентов гуманитарных и педагогических специальностей очной формы обучения
• Дата: 27.10.2020
• Размер: 1.82 Mb.
• Имя файла: Математика и информатика.doc
• Тип: Учебное пособие; #146041
• страница: 7 из 12

Глава 6. Статистические оценки параметров распределения

Математическая статистика возникла в XVII в. и развивалась параллельно с теорией вероятностей. Большой вклад в развитие математической статистики внесли российские ученые в XIX в. – начале XX в.: в первую очередь П.Л. Чебышев, А.А. Марков, А.М. Ляпунов, а также учёные других стран – К. Гаусс, К. Пирсон, Ф. Гальтон и т.д.

В XX в. существенный вклад в развитие математической статистики был сделан советскими математиками, в частности, А.Н. Колмогоровым, В.И. Романовским, Е.Е. Слуцким, Н.В.Смирновым, а также английскими – Стьюдентом, Р. Фишером, Э. Пирсоном и американскими учёными – Ю. Нейманом, А. Вальдом и др.

6.1. Предмет и задачи математической статистики

Теория вероятностей изучает математические модели случайных явлений, при этом сама математическая модель считается заданной. В задачах теории вероятностей исходят из того, что задано вероятностное пространство, множество элементарных исходов и вероятность любого события.

Так, например, если изучается некоторое случайное событие А, то известно Р(А). Если же речь идёт о случайной величине Х, то известен закон распределения вероятностей в какой-либо форме и, как следствие, числовые характеристики исследуемой случайной величины.

В практических задачах эти характеристики, как правило, неизвестны, но имеются некоторые экспериментальные данные о событии или случайной величине. Требуется на основании этих данных построить подходящую вероятностную модель изучаемого явления, то есть приближённо оценить неизвестные закон распределения и числовые характеристики исследуемой случайной величины на основе экспериментальных данных. Это и является задачей математической статистики. В математической статистике единственный объект это данные эксперимента. Результаты эксперимента выражаются значениями некоторой случайной величины.

В теории вероятностей вероятностное пространство задано и требуется предсказать возможное поведение случайной величины. В математической статистике наоборот, известны лишь результаты (значения случайной величины), по которым восстанавливается вероятностное пространство. По экспериментальным данным строится вероятностная модель явления, соответствующая этим данным, т.е. интерпретация данных.

Математической статистикой называется наука, занимающаяся методами обработки экспериментальных данных, полученных в результате наблюдений над случайными явлениями. Первая задача математической статистики: указать способы сбора и группировки статистических данных, полученных в результате экспериментов. Вторая задача математической статистики: разработать методы анализа статистических данных.

Ко второй задаче относятся:

1. 
   Оценка неизвестных параметров (вероятности события, функции распределения и её параметров и т.д.) с построением доверительных интервалов (методы оценивания).
   
2. 
   Проверка статистических гипотез о виде неизвестного распределения и параметров распределения (методы проверки гипотез).
   

При этом решаются следующие в порядке сложности и важности задачи:

• 
  Описание явлений, то есть, упорядочение поступившего статистического материала, представление его в наиболее удобном для обозрения и анализа виде (таблицы, графики).
  
• 
  Анализ и прогноз, то есть приближённая оценка характеристик на основании статистических данных. Например, приближённая оценка математического ожидания и дисперсии наблюдаемой случайной величины и определение погрешностей этих оценок.
  
• 
  Выработка оптимальных решений. Например, определение числа опытов n, достаточного для того, чтобы ошибка от замены теоретических числовых характеристик их экспериментальными оценками не превышала заданного значения. В связи с этим возникает задача проверки правдоподобия гипотез о параметрах распределения и о законах распределения случайной величины, решением которой является возможность сделать один из выводов:
  

– отбросить гипотезу, как противоречащую опытным данным;

– принять гипотезу, считать ее приемлемой.

Математическая статистика помогает экспериментатору лучше разобраться в опытных данных, полученных в результате наблюдений над случайными явлениями; оценить, значимы или не значимы наблюдаемые факты; принять или отбросить те или иные гипотезы о природе случайных явлений.

6.2. Выборочный метод

6.2.1 Полигон и гистограмма

Генеральной совокупностью называют полный набор всех возможных N значений дискретной случайной величины Х. Практически сложно получить полную информацию о случайной величине. Поэтому случайным образом отбирают объекты, которые называется выборкой, при этом число – n называется объёмом выборки. Выборку делают либо из ранее полученных результатов, либо планируют эксперимент. По результатам выборки строят простой статистический ряд в виде таблицы, состоящей из двух строк, в первой – порядковый номер измерения, во второй – его результат x_i. Затем производят группировку данных. Вначале x_i располагают в порядке возрастания, интервал наблюдаемых значений случайной величины разбивают на последовательные непересекающиеся частичные интервалы, далее подсчитывают количество значений x_i, попавших в каждый интервал, т.е. n_i. Таким образом, получается группированный статистический ряд или статистическое распределение выборки.

Статистическим распределением выборки или статистическим рядом называют перечень вариант и соответствующих им частот или относительных частот.

Пример 1. После группировки данных в выборке статистический ряд задан таблицей 6.1 (где объём выборки n = 15).

Таблица 6.1

i	1	2	3	4
xi	2	3	5	10
ni	5	5	3	2

В таблице 6.1 значения x_i называют вариантами. Последовательность вариант, записанных в возрастающем порядке (вся строка x_i) называется вариационным рядом. Число наблюдений n_i называют частотами, i – номер варианты.

Учитывая, что



n – это объем выборки, можно найти относительную частоту p_i=n_i/n, наблюдаемого значения x_i – варианты, k – количество вариант.

Тогда таблица 6.1 будет иметь вид:

Таблица 6.2

i	1	2	3	4
xi	2	3	5	10
ni/n	0,33	0,33	0,2	0,14

Табличные данные могут быть представлены графически в виде полигона или гистограммы. Если выборка задана в виде отдельных точек, а не интервалов, тогда строят полигон частот. Полигоном частот называется ломанная, отрезки которой соединяют точки (x; n_i/n). На рис. 6.1 изображен полигон относительных частот, приведённых в таблице 6.2.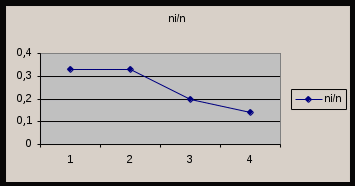



Рис. 6.1. Полигон

Пример 2.

В этом примере наблюдаемые значения случайной величины после группировки данных в выборке разбиты на последовательные непересекающиеся частичные интервалы. В результате получается статистический ряд, который задан таблицей 6.3.

Таблица 6.3

i	1	2	3	4
xi	02	24	46	68
ni	5	10	12	3

Данную таблицу можно представить через относительную частоту p_i =n_i/n (где объём выборки n = 30) в таблице 6.4.

Таблица 6.4

i	1	2	3	4
xi	02	24	46	68
рi=ni/n	0,17	0,33	0,4	0,1

При этом частоты р_i удовлетворяют условию

=1.

Если выборка задана в виде интервалов, тогда строят гистограмму.

Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат интервалы x_i, их высоты равны р_i =n_i/n (плотности относительной частоты). На рис. 6.2 изображена гистограмма относительных частот, приведённых в таблице 6.4.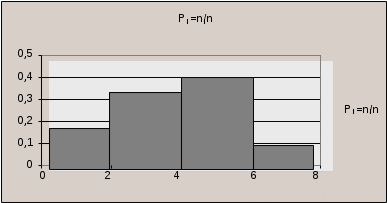



Рис. 6.2. Гистограмма

6.2.2. Эмпирическая функция распределения

Понятие функции распределения было дано в разделе теории вероятности для случайной величины. Для выборки вводится понятие эмпирической функции распределения. Эмпирическая функция распределения (функция распределения выборки) это функция F^*(x), которая определяет для каждого значения x_i относительную частоту события X

,

(6.1)

где: n_x – число вариант меньших х, n – объём выборки.

В отличие от эмпирической функции распределения для выборки, вводится понятие теоретической функции распределения для генеральной совокупности – F(x). Теоретическая функция распределения определяет вероятность события X*(x) по вероятности стремится к теоретической функции распределения F(x) при больших количествах испытаний и обладает всеми свойствами F(x):

1. 
   Значения эмпирической функции принадлежат отрезку F^*(x)  [0;1].
   
2. 
   F^*(x) – неубывающая функция.
   
3. 
   Если х₁ – наименьшая варианта, то F^*(x)=0 при x ≤ x₁.
   
4. 
   Если х_k – наибольшая варианта, то F^*(x)=1 при x > x_k.
   

Пример 3.

Учитывая свойства 1, 2, 3, найдём эмпирическую функцию распределения для примера 1.

Решение.

Объём выборки n=15.

Наименьшая варианта х₁=2, тогда: F^*(x)=0 при x ≤ x₁.

При значениях варианты в интервале 2*(x)=5/15=0,33.

При значениях варианты в интервале 3*(x)=10/15=0,66.

При 5*(x)=13/15 = 0,87.

При x>10: F^*(x) =1.

Эмпирическая функция распределения представлена в таблице 6.5.

Таблица 6.5

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14
xi	<2	2	>2	3	>3	4	5	>5	6	7	8	9	10	>10
F*(x)	0	0	0,33	0,33	0,66	0,66	0,66	0,87	0,87	0,87	0,87	0,87	0,87	1

На рис. 6.3 представлен график эмпирической функции распределения.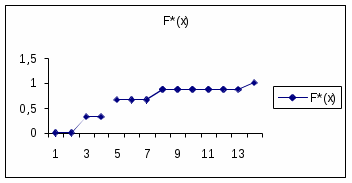



Рис. 6.3. Эмпирическая функция распределения

6.3. Статистические оценки параметров распределения

Пусть дискретная случайная величина Х задана генеральной совокупностью. Требуется оценить количественные характеристики заданной совокупности: математическое ожидание, дисперсию и установить функцию распределения дискретной случайной величины Х. Обычно практически известны лишь данные выборки. Через эти данные следует оценить количественные характеристики дискретной случайной величины Х.

Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Статистические оценки параметров распределения должны удовлетворять следующим требованиям: состоятельности, несмещённости, эффективности.

Состоятельной называют статистическую оценку, которая при неограниченном увеличении числа наблюдений стремится по вероятности к оцениваемому параметру.

Несмещённой называют статистическую оценку, если её математическое ожидание равно оцениваемой характеристике независимо от числа наблюдений. Несмещённая статистическая оценка называется эффективной, если она имеет минимально возможную дисперсию.

Генеральная средняя и выборочная средняя

Пусть задана дискретная случайная величина Х в виде генеральной совокупности. Генеральной средней называют среднее арифметическое значений признака генеральной совокупности:

.

(6.2)

где x_i – варианта генеральной совокупности, n_i – частота варианты x_i,

.

N – все возможные значения частот дискретной случайной величины Х.

В частном случае, когда генеральная совокупность содержит по одному значению каждой варианты, генеральная средняя равна:

.

(6.2а)

Если рассматривать значения Х генеральной совокупности как случайную величину, то математическое ожидание М(Х) равно генеральной средней М(Х)= x_г, а генеральная средняя определяется как математическое ожидание:

x_г = М(Х).

Пусть извлечена выборка объема n из генеральной совокупности относительно количественного признака X. Выборочной среднейx называется среднее арифметическое значение признака выборочной совокупности.

,

(6.3)

где

.

В частном случае, когда выборка содержит по одному значению каждой варианты, выборочная средняя равна:

.

(6.3а)

Аналогично генеральной совокупности можно сделать вывод относительно выборочной средней. Если рассматривать значения Х выборки, как случайную величину, то математическое ожидание m(Х) равно выборочной средней:

.

(6.4)

Генеральной дисперсией называют среднее арифметическое квадратов отклонения значений признака X от их среднего значения x_г. Рассеяние значений количественного признака X в выборке вокруг своего среднего значенияx характеризует выборочная дисперсия. Выборочной дисперсией D_в называется среднее арифметическое квадратов отклонения значений признака X от их среднего значения .

.

(6.5)

В частном случае, когда выборка содержит по одному значению каждой варианты, выборочная дисперсия равна:

.

(6.5а)

Пример 4.

Выборочная совокупность задана таблицей распределения в примере 1.

Таблица 6.6

i	1	2	3	4
xi	2	3	5	10
ni	5	5	3	2

Найти выборочное математическое ожидание, дисперсию, среднеквадратическое отклонение для распределения, заданного таблицей 6.6.

Решение.

Выборочная средняя вычисляется по формуле (6.4):



Выборочная дисперсия D_в вычисляется по формуле (6.5):



Выборочное среднее квадратическое отклонение: .

В задачах выборочная совокупность может быть задана таблицей распределения с относительной частотой. Рассмотрим пример 4, заменив в таблице 6.6 последнюю строку относительной частотой p_i=n_i/n. В примере n=15. Выборочная дисперсия D_в вычисляется по данным таблицы 6.7.

Таблица 6.7

i	1	2	3	4
xi	2	3	5	10
pi	P1 =5/15	P2 =5/15	P3 =3/15	P4 =2/15

Выборочная дисперсия D_в может быть вычислена как с использованием относительной частоты, так и абсолютной частоты.



Характеристики случайной величины, построенные на основании выборочных данных, называются выборочными или точечными оценками.

Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные в примере 4, являются точечными.

6.4. Некоторые статистические распределения

При обработке статистических данных результаты сравнивают со статистикой, результаты которой известны. С помощью такой статистики можно получить информацию о случайной величине из выборки. В результате, только на основании выборочных данных можно получить случайную величину с известным законом распределения. Многие важные статистики распределены по специальным законам. К ним относятся:

• 
  Распределение ² « Хи – квадрат».
  
• 
  Распределение Стьюдента.
  

6.4.1. ² – распределение

Пусть ₁, ₂,…, _k – независимые случайные величины, распределенные по стандартному нормальному закону – N (0,1), т.е. математическое ожидание равно нулю, а среднее квадратическое отклонение равно единице. Сумма квадратов этих случайных величин равна:

.

(6.6)

Сумма квадратов этих случайных величин в (6.6) распределена по закону ² «Хи – квадрат» с k=n степенями свободы.

Эту случайную величину обозначают ² (k):

.

Если случайную величину принять за х, то можно записать:

2 (k) = x12 + x22 + ... + xk2.

(6.6a)

Если же эти величины связаны одним линейным соотношением, например:

,

то число степеней свободы k = n – 1. Среднее значение равно:

.

Свойства ² –распределения:

1. 
   Случайная величина ²(k) имеет нулевую плотность распределения при х ≤ 0, так как данная величина есть сумма квадратов и всегда положительна.
   
2. 
   При большом числе степеней свободы k распределение ² (k) близко к нормальному. В этом случае математическое ожидание случайной величины распределенной по закону ² (с k степенями свободы) равно k:
   

M2(k) = k.

(6.7)

6.4.2. Распределение Стьюдента

Пусть случайная величина  распределена по стандартному нормальному закону N(0,1). Случайную величину  делят на корень из ²/k.

Закон Стьюдента – это отношение нормированной случайной величины  к квадратному корню из независимой случайной величины, распределенной по закону «Хи – квадрат» с k степенями свободы, делённой на k. Данная случайная величина и соответствующий закон распределения обозначаются через t(k), именуются «распределение Стьюдента»:

.

(6.8)

График плотности распределения Стьюдента похож на график нормального распределения, приведённого на рис 5.4. С увеличением k – степеней свободы кривая вытягивается вдоль оси y.

Свойства распределения Стьюдента:

Свойство 1. Распределение Стьюдента симметрично относительно оси Y, причём M t(k) = 0.

Свойство 2. При больших значениях k распределение Стьюдента близко к стандартному нормальному распределению N(0,1).

6.5. Интервальные оценки

В разделе 6.3 на примерах было показано определение выборочных числовых характеристик случайной величины: выборочной средней –x, выборочной дисперсии – D_в, выборочного среднего квадратического отклонения – _в. Полученные оценки являются приближенными. Поэтому вводится понятие интервальных оценок.

Интервальной называют оценку, которая определяется границами: началом и концом диапазона значений характеристики. Интервальные оценки позволяют установить точность и надёжность оценок. Однако граничные значения также случайные величины. Следовательно, строится интервал со случайными границами, который с заданной вероятностью содержал бы неизвестное значение параметра распределения.

Для определения погрешности полученных значений используют интервальные оценки, применяя понятие «доверительного интервала» – интервала, внутри которого параметр, как ожидается, найдется с некоторой доверительной вероятностью (надёжностью) . Иногда вместо  используют величину  = 1 – , называемую уровнем значимости. На практике уровнь значимости – малое число, которое принимается примерно равным:

 = 0,01;  =0,05;  = 0,1.

6.5.1. Доверительные интервалы для оценки математического ожидания нормального распределения случайной величины

Доверительным называют интервал (^*–,^*+ ), который покрывает неизвестный параметр с заданной надёжностью , где, ^* – статистическая характеристика, найденная по данным выборки, которая служит оценкой неизвестного параметра . Отклонение неизвестного параметра  от его оценки ^* задаётся величиной положительной >0,так как их разность задаётся по модулю | – ^*| < . Чем меньше отклонение , тем точнее оценка. Рассмотрим нахождение доверительного интервала для математического ожидания нормально распределенной случайной величины. Из теории вероятностей интервальные вероятности для нормального распределения N(a,) определяются формулой (5.20):

P (|X– a| ≤ ) = 2Ф(/) = 2Ф(t),

(6.9)

где t = /.

Пусть случайая величина Х генеральной совокупности распределена нормально. Требуется оценить неизвестное математическое ожидание по выборочной средней. Выборочную среднюю можно рассматривать как случайую величину, которая изменяется от выборки к выборке.

Из теории вероятностей дискретной случайной величины известны положения для числовых характеристик среднего арифметического. В частности:

1. 
   Дисперсия среднего арифметического n одинаково распределённых взаимно независимых случайных величин в n раз меньше дисперсии D каждой из величин:
   

.

2. 
   Среднее квадратическое отклонение n одинаково распределённых взаимно независимых случайных величин соответственно равно:
   

.

Заменив в (6.9) случайую величину Х на выборочную среднююx,  на



можно (6.9) переписать в виде:

,

(6.9а)

где:

.

Можно найти отклонение неизвестного параметра от его оценки:

.

(6.10)

Если в (6.9а) рассмотреть неравенство , то из него можно выразить неизвестное математическое ожидание а:

.

(6.11)

Если в (6.11) подставить вместо  значение из (6.10), то получим доверительный интервал для математического ожидания нормально распределенной случайной величины.

.

(6.12)

Вероятность



определяется законом нормального распределения, если известна дисперсия D=².

Если дисперсия неизвестна, а лишь подсчитано ее несмещённое значение

,

то вероятность



определяется законом распределения Стьюдента со степенями свободы k = n–1. С увеличением степеней свободы k, то есть с увеличением объема выборки, распределение Стьюдента стремится к нормальному.

6.5.2. Доверительные интервалы для математического ожидания при известной дисперсии

Пусть случайая величина Х генеральной совокупности распределена нормально, учитывая, что дисперсия и среднее квадратическое отклонение  этого распределения известны. Требуется оценить неизвестное математическое ожидание по выборочной средней. В данном случае задача сводится к нахождению доверительного интервала для математического ожидания с надёжностью . Если задаться значением доверительной вероятности (надёжности) , то можно найти вероятность попадания в интервал для неизвестного математического ожидания, используя формулу (6.9а):

(6.13)

где  – вероятность покрытия математического ожидания а доверительным интервалом .

Если приравнять правые части (6.9а) и (6.13), то получим:

 = 2Ф(t).

(6.14)

где Ф(t) – функция Лапласа (5.17а).

В результате можно сформулировать алгоритм отыскания границ доверительного интервала для математического ожидания, если известна дисперсия D = ²:

1. 
   Задать значение надёжности – .
   
2. 
   Из (6.14) выразить Ф(t) = 0,5. Выбрать значение t из таблицы для функции Лапласа по значению Ф(t) (см. Приложение 1).
   
3. 
   Вычислить отклонение  по формуле (6.10).
   
4. 
   Записать доверительный интервал по формуле (6.12) такой, что с вероятностью  выполняется неравенство:
   

.

(6.15)

Пример 5.

Случайная величина Х имеет нормальное распределение. Найти доверительные интервалы для оценки с надежностью  = 0,96 неизвестного математического ожидания а, если даны:

1) генеральное среднее квадратическое отклонение  = 5;

2) выборочная средняя ;

3) объём выборки n = 49.

Решение.

В формуле (6.15) интервальной оценки математического ожидания а с надёжностью  все величины, кроме t, известны. Значение t можно найти, используя (6.14):  = 2Ф(t) = 0,96. Ф(t) = 0,48.

По таблице Приложения 1 для функции Лапласа Ф(t) = 0,48 находят соответствующее значение t = 2,06. Следовательно, . Подставив в формулу (6.12) вычисленное значение , можно получить доверительный интервал: 30-1,47 < a < 30+1,47.

Искомый доверительный интервал для оценки с надёжностью  = 0,96 неизвестного математического ожидания равен: 28,53 < a < 31,47.

6.5.3. Оценка генеральной дисперсии по исправленной выборочной

Пусть из генеральной совокупности объёмом n извлечена выборка. Требуется по данным выборке оценить неизвестную генеральную дисперсию D_г.

Выборочная дисперсия является смещённой оценкой генеральной дисперсии. Отличие математического ожидания выборочной дисперсии от оцениваемой генеральной дисперсии определяется следующим соотношением:

.

(6.16)

Выборочная дисперсия может быть исправлена. Исправленная выборочная дисперсия равна:

.

(6.17)

Исправленная выборочная дисперсия (6.17) является несмещённой оценкой генеральной дисперсии. Таким образом, получена оценка генеральной дисперсии по исправленной выборочной дисперсии.

6.5.4. Доверительные интервалы для математического ожидания при неизвестной дисперсии

Пусть случайая величина Х генеральной совокупности распределена нормально, учитывая, что дисперсия неизвестна. Требуется оценить неизвестное математическое ожидание с помощью доверительных интервалов.

Во-первых, по данным выборки объёмом n можно найти исправленную выборочную дисперсию s², используя (6.17).

Во-вторых, по данным выборки можно строить случайную величину, которая имеет распределение Стьюдента с k = n–1 степенями свободы, используя формулу (6.8):

.

(6.18)

Если сравнить распределение Стьюдента по данным выборки (6.18) с (6.8), то следует отметить, что в (6.18):

1. 
   За случайную величину  принята разность ( ), которая является отклонением неизвестного математического ожидания а от среднего выборочного.
   
2. 
   За ² принимается исправленная выборочная дисперсия s².
   

Если в числителе (6.18) заменить разность ( ) на , то (6.18) можно записать в виде:

.

(6.19)

Из уравнения (6.19) можно найти  – отклонение неизвестного математического ожидания от среднего выборочного:

.

(6.20)

Из уравнения (6.18) можно найти неизвестное математическое ожидание, если известно значение случайной величины t_, по (6.19), где индекс переменной указывает на особенность задачи с использованием понятия надёжности  в отличие от (6.8). Математическое ожидание записывается в виде доверительного интервала, подставив отклонение  из выражения (6.20) в неравенство (6.11):

.

(6.21)

Если задаться значением надёжности , то можно найти вероятность попадания в интервал для неизвестного математического ожидания, который строится по аналогии с (6.15):

.

(6.22)

Из уравнений (6.8) и (6.19) видно, что распределение Стьюдента определяется параметром n – объёмом выборки (числом степеней свободы k=n–1) и не зависит от неизвестных параметров а и . Эта особенность является его большим достоинством.

Можно сформулировать алгоритм отыскания границ доверительного интервала для математического ожидания, если неизвестна дисперсия D = ²:

1. 
   Задают значение надёжности в формуле (6.22) – .
   
2. 
   Находят значение t_, пользуясь таблицей Приложения 2 по значениям k и уровню значимости  = 1– , выбрав верхний вариант: [Уровень значимости  (двусторонняя крит. область)].
   
3. 
   Из уравнения (6.20) находят отклонение неизвестного математического ожидания от среднего выборочного – .
   
4. 
   Строится доверительный интервал по (6.21) или (6.11), содержащий неизвестное математическое ожидание с вероятностью .
   

Пример 6.

Случайная величина Х имеет нормальное распределение. По выборке объёма n=61 найдена выборочная средняяx =30 и исправленное среднее квадратическое отклонение s = 1,5. Найти доверительный интервал для оценки с надёжностью =0,95 неизвестного математического ожидания – а.

Решение. Дано по условию задачи:

1. 
   Исправленное среднее квадратическое отклонение s = 1,5.
   
2. 
   Выборочная средняяx =30.
   
3. 
   Надёжность  = 0,95;
   
4. 
   Объём выборки n = 61.
   

Пользуясь таблицей приложения 2 по значениям k = n – 1 = 60 и уровню значимости  = 1 –  = 1–0,95 = 0,05 находим значение t_=2,00.

Вычисляем по формуле (6.20):

Полученное значение  подставим в формулу доверительного интервала (6.11): 30 – 0,387 < a < 30+ 0,387.

Доверительный интервал для неизвестного математического ожидания с надёжностью  = 0,95 равен: 29,613 < a < 30,387.