Учебное пособие Теории отраслевых рынков
 Скачать 1.74 Mb. Скачать 1.74 Mb.
|
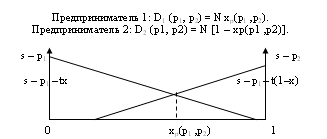 . Когда, например, p2 - р1 ≥ t, то товар предпринимателя 2 спросом не пользуется. Функция спроса предпринимателя 1: если p1 ≤ s - t, то D1 (p1, p2) = N. 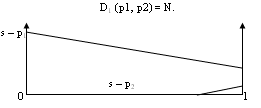 Если p1 ≥ s - t, то D1 (p1, p2) = N(s - p1) / t . 3. Когда p1 и р2 находятся в интервале [s-t, s], каждый из предпринимателей обладает локальной монопольной властью. Функции спроса: D1 (p1, p2) = N(s - p1) / t; D2 (p1, p2) = N(s - p2) / t. Часть потребителей совсем не покупает товар (рынок не покрыт). 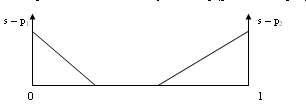 III.4 Равновесие горизонтальной дифференциации Примем в модели линейного города общее число покупателей за 1. Транспортные расходы t являются линейной функцией. Спрос на продукцию предпринимателя 1: D1 = N хр(p1 ,р2) = хр(p1 ,р2) = (p2 - р1 + t) / 2 t; спрос на продукцию предпринимателя 2: D2 (p1, p2) = N [1 - хр(p1 ,р2)] = 1 - хр(p1 ,р2) = (р1 - p2 + t) / 2 t. Прибыль предпринимателей, при условии равенства издержек с, составит: П1 (p1, p2)= (р1 - с) [(p2 - р1 + t) / 2 t ]; П2 (p1, p2)= (р2 - с) [(p1 - р2 + t) / 2 t ]. Max{П1 (p1, p2)}. Условие первого порядка p2 + с + t - 2р1 = 0; Max{П2 (p1, p2)}. Условие первого порядка p1 + с + t - 2р2 = 0. Если в результате конкуренции цены предпринимателей уравняется и снизится до минимально возможного уровня, то они будут равны: p1 = p2 = с + t = рс + t. Прибыли предпринимателей при продуктовой дифференциации составят: П1 =П2 = t / 2 То есть, несмотря на конкуренцию, предпринимателям удается получить некоторую степень монопольной власти над потребителями, для которых они являются ближайшими поставщиками, повысить цену и получать экономические прибыли. Размер прибыли тем выше, чем больше транспортные расходы или оценка потребителями времени, необходимого для осуществления покупок. Упражнение Предприниматели расположены в противоположных концах города. Транспортные затраты линейны по расстоянию. Предельные издержки предпринимателей с1 и с2 (с1 ≠ с2). Определите: функции реагирования рi = Ri (pj), функции цен равновесия Нэша pi(ci,cj) и редуцированную функцию прибыли Пi (ci,cj) от предельных издержек предпринимателей. III.5 Горизонтальная дифференциация в условиях конкуренции (модель кругового города) Представим город, жители которого равномерно распределены по окружности длиной 1. В этом случае не существует местоположения, которое a priori было бы лучше другого. Плотность распределения единична по всей окружности. Предприниматели также располагаются по окружности. Потребители приобретают единицу товара и имеют удельные транспортные затраты t. Каждый предприниматель может занимать только одно местоположение. Вход на рынок свободен. При входе предприниматель несет постоянные затраты f. Предельные издержки равны с. Прибыль фирмы i составляет (pi - с)Di - f, если она входит на рынок. Число предпринимателей, вступающих на рынок равно n. Они автоматически располагаются равноудаленно друг от друга по окружности. Таким образом, предприниматели максимально дифференцируются. Фирмы при заданном местоположении ведут ценовую конкуренцию. В равновесии Нэша симметрично расположенные предприниматели, назначают одинаковую цену р. Вновь входящая фирма i имеет только двух действительных соперников, расположенных по соседству. Если она назначает цену рi, то потребитель, расположенный на расстоянии х, принадлежащим интервалу [0, 1/ n], от фирмы i, безразличен к покупке у фирмы i или у ее ближайшего соседа, если pi + tx = p + t(1/n -х).  Рис. Круговой город Спрос на продукцию фирмы i : Di (pi ,p) = 2x = (p + t/n - pi) / t. Фирма i максимизирует прибыль: Пi (pi ,p) = (pi -c)[ (p + t/n - pi) / t] - f. При установлении равновесия Нэша предприниматель, вошедший на рынок, установит цену pi = p = с + t/n Результат аналогичен результату, полученному для линейного города. Величина прибыли уменьшается вместе с ростом числа фирм. В равновесии на рынке число фирм увеличивается до тех пор, пока (р - с) 1/n - f не станет равным 0. (р - с) 1/n - f = t/n2 - f = 0 Следовательно, количество фирм и рыночная цена в случае несовершенной конкуренции со свободным входом будут соответственно 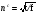 , pc = c + f. , pc = c + f.Цены фирм превышают предельные затраты. Вследствие наличия конкуренции добавка к цене становится равной постоянным затратам. Возможность дифференциации зависит от величины постоянных затрат и транспортных расходов. Количество предпринимателей при высоких постоянных затратах число фирм меньше, чем при низких. Когда затраты на вход или постоянные затраты становятся незначительными, количество фирм увеличивается настолько, что цена приближается к предельным издержкам. Увеличение транспортных затрат (оценки потребителем времени, необходимого для совершения покупки) увеличивает количество фирм. Оптимальное количество предпринимателей с точки зрения общества может быть определено исходя из критериев минимизации транспортных расходов потребителей и величины суммарных постоянных расходов предпринимателей: 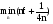 . . 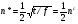 . В рыночной системе функционирует в два раза больше фирм. . В рыночной системе функционирует в два раза больше фирм. Это свидетельствует о более высокой степени горизонтальной дифференциации продуктов, чем это необходимо для обеспечения социально оптимального уровня. III.6 Информативная дифференциация Рассмотрим линейный город протяженностью 1. Предприниматели 1 и 2 продают одинаковый продукт и дифференцируются по направлениям информации и размещения. Они расположены на противоположных концах города и случайным образом рассылают рекламные объявления. Реклама содержит информацию о существовании товара и его цене. Они не могут проводить ценовую дискриминацию и устанавливают цены р1 и р2 соответственно. Потребители расположены равномерно по всей длине с плотностью 1 и несут транспортные затраты t на единицу расстояния. Потребитель имеет единичный спрос на продукт. Потребители поиском товара не занимаются и могут приобрести товар только получив рекламное объявление соответствующего предпринимателя. Оценка полезности товара потребителем равна |
