механика. 2015 гМет.ПМ. уфимский государственный нефтяной технический университет
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
|
ЗАДАНИЕ №4 РАСЧЕТ НА ПРОЧНОСТЬ БАЛОК ПРИ ИЗГИБЕ Методические рекомендации к решению задач Приступая к решению задач необходимо рассмотреть следующие вопросы из теоретического материала данной темы. 1 Общие понятия. Прямой поперечный изгиб, поперечная сила, изгибающий момент. 2 Основные правила построения эпюры поперечной силы и изгибающего момента. 3 Главные напряжения при прямом поперечном изгибе. 4 Расчеты на прочность при изгибе. Вопросы для самопроверки 1 Как находится изгибающий момент, в каком -либо сечении балки? 2 В каком случае изгибающий момент считается положительным? 3 Как находится поперечная сила, в каком либо сечении балки? 4 Когда поперечная сила считается положительной? 5 Какая зависимость имеется между величинами М и Q ? 6 Как находят максимальный изгибающий момент? 7 Какой случай изгиба называется чистым изгибом? 8 По какой кривой изогнется балка в случае чистого изгиба? 9 Как изменяются нормальные напряжения по высоте балки? 10 Что называется нейтральным слоем и где он находится? 11 Что называется моментом сопротивления при изгибе? Задачи на прямой изгиб необходимо решать в следующей последовательности: 1 Балку разделить на участки по характерным сечениям. 2 Определить вид эпюры поперечных сил на каждом участке в зависимости от внешней нагрузки, вычислить поперечные силы в характерных сечениях и построить эпюру поперечных сил. 3 Определить вид эпюры изгибающих моментов на каждом участке в зависимости от внешней нагрузки, вычислить изгибающие моменты в характерных сечениях и построить эпюру изгибающих моментов. 4 Для данной балки, имеющей по всей длине постоянное поперечное сечение, выполнить проектный расчет, т.е. определить Wx в опасном сечении, где изгибающий момент имеет наибольшее по модулю значение. 42 План решения задачи 1 Вычертить схему нагружения балки (принять 1=6м). 2 Построить эпюры поперечной силы Q и изгибающего момента Мизг. 3 Подобрать круглое сечение, прямоугольное сечение (с отношением высоты к ширине, равное 2) и двутавровое сечение (материал балки - Ст.З). 4 Сравнить вес одного погонного метра длины каждого профиля. 5 Построить эпюру нормальных напряжений в опасном сечении двутавровой балки. Таблица 4.1 Рисунок 4.1 Таблица 4.1 Числовые данные
43 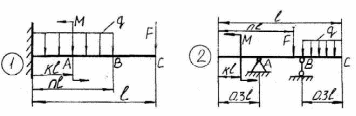 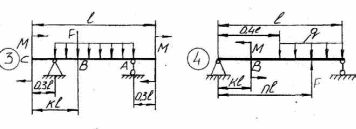 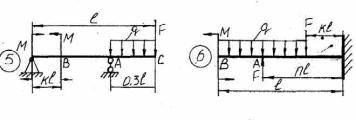 Рисунок 4.1 – Схемы нагружения балок 44 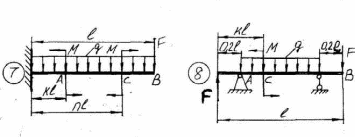 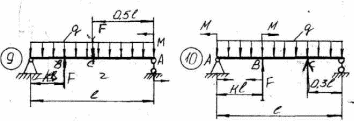 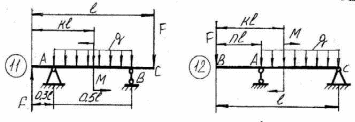 Рисунок 4.1 – Продолжение. 45 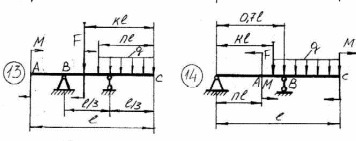 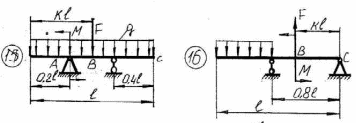 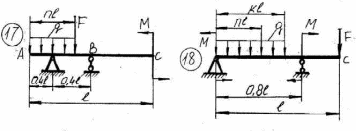 Рисунок 4.1 – Продолжение. 46 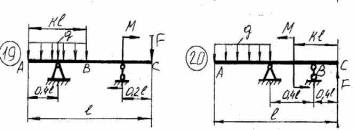 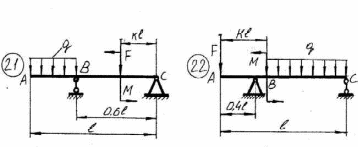 Рисунок 4.1 – Продолжение. 47 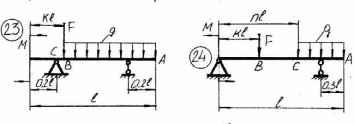 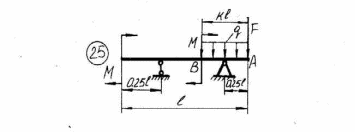 Рисунок 4.1 – Окончание. 48 ЗАДАНИЕ №5 РАСЧЕТ ВАЛА НА ИЗГИБ С КРУЧЕНИЕМ Методические рекомендации к решению задач Приступая к решению задач, необходимо рассмотреть следующие вопросы из теоретического материала данной темы. 1 Сложное сопротивление. Косой изгиб. Изгиб с кручением брусьев круглого сечения. 2 Определение крутящих, изгибающих моментов, поперечных сил при одновременном действии деформации кручения и изгиба. 3 Построение эпюр внутренних усилий – суммарный изгибающий момент. 4 Расчеты на прочность в случае изгиба с кручением. Вопросы для самопроверки 1 Какой случай изгиба называется косым изгибом? 2 Возможен ли косой изгиб при чистом изгибе? 3 В каких точках поперечного сечения возникают наибольшие напряжения при косом изгибе? 4 Как находится положение нейтральной линии при косом изгибе? 5 Как пройдет нейтральная линия, если плоскость действия сил совпадает с диагональной плоскостью балки прямоугольного поперечного сечения? 6 Как определяются деформации при косом изгибе? 7 Может ли балка круглого поперечного сечения испытывать косой изгиб? 8 Какие напряжения возникают в поперечном сечении стержня при изгибе с кручением? 9 Как находятся опасные сечения стержня при изгибе с кручением? 10 В каких точках круглого поперечного сечения возникают наибольшие напряжения при изгибе с кручением? Почему обыкновенно не учитывают касательные напряжения от изгиба при совместном действии изгиба и кручения? Задачи на изгиб с кручением необходимо решать в следующей последовательности: 1 Привести нагрузки, действующие на вал к его оси, освободить вал от опор, заменив их действие реакциями в вертикальной и горизонтальной плоскостях. 2 По заданной мощности Р и угловой скорости ω определить вращающие моменты, действующие на вал. 3 Вычислить нагрузки F1, Fr1, F2, Fr2, приложенные к валу. 4 Составить уравнения равновесия всех сил, действующих на вал, отдельно в 49 вертикальной плоскости и отдельно в горизонтальной плоскости и определить реакции опор в обеих плоскостях. 5 Построить эпюру крутящих моментов. 6 Построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях (эпюры Mx, My). 7 Определить наибольшее значение эквивалентного момента: 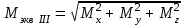 Или 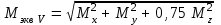 . .8 Положив экв = [], определить требуемый осевой момент сопротивления: 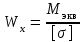 , для сплошного круглого сечения определяем d по , для сплошного круглого сечения определяем d по формуле  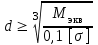 План решения задачи 1 Определить мощность на шкиве, где она не задана. 2 Определить моменты, передаваемые каждым шкивом. 3 Построить эпюру крутящих моментов. 4 Определить давление, передаваемое шкивами на вал, считая, что натяжение ведущего ремня в два раза больше, чем натяжение ведомого. 5 Показать на схеме в аксонометрии расположение усилий, действующих на вал и разложив их по осям, определить вертикальные и горизонтальные составляющие. 6 Построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях и эпюру суммарного изгибающего момента. 7 Определить диаметр вала, пользуясь четвертой теорией прочности, если [G]=110 МПа; а=0,2 м. Диаметры шкивов соответственно равны: D1=180 мм; D2=160 мм; D3=140 мм; D4=200 мм. Таблица 5.1 Рисунок 5.1 50 Таблица 5.1 Числовые данные
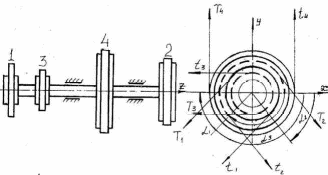 Рисунок 5.1 – Схемы нагружения валов 51 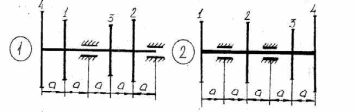 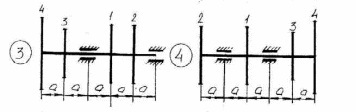 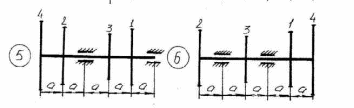 Рисунок 5.1 – Продолжение 52 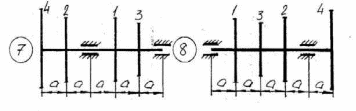 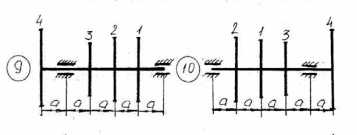 Рисунок 5.1 – Продолжение 53 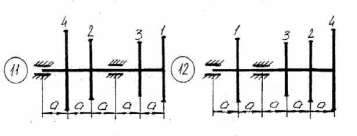 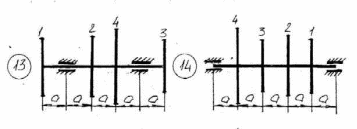 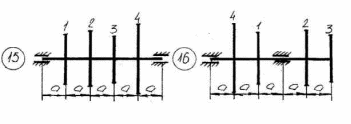 Рисунок 5.1 – Продолжение 54 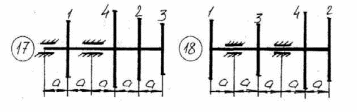 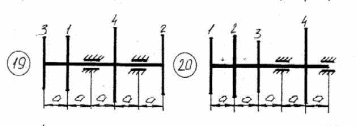 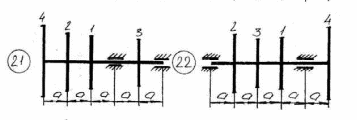 Рисунок 5.1 – Продолжение 55 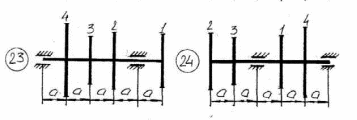 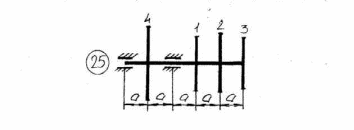 Рисунок 5.1 – Окончание. 56 СПИСОК ЛИТЕРАТУРЫ 1 Прикладная механика: учеб. пособие для вузов / В.Т. Батиенков.- М.: РИОР: Инфра-М, 2011. 2 Теоретическая механика. Сопротивление материалов: учеб. пособие/ Эрдеди А.А., Эрдеди Н.А. – 12-е изд. - М.: Академия, 2011.-320 с. 3 Прикладная механика: учебник для вузов/ Джамай В.В.-М.: Дрофа, 2004. 4 Сопротивление материалов: учеб. пособие/ Берёзина Е.В. – М.: Инфра – М, 2012 5 Сопротивление материалов: учеб. пособие для вузов/под ред. Н.А. Костенко. – М.: Высшая школа, 2007 6 Теоретическая механика: учебник/ Е.А. Митюшов, С.А. Берестова. – 2-е изд., перераб. – М.: Академия, 2011. – 320 с. – (Высшее профессиональное образование, бакалавриат). 7 Краткий курс теоретической механики: в теории, задачах и плакатах: учебник для вузов/ Сорокин В.В. – М.: Интер, 2005. – 600 с. 8 Курс теоретической механики: учебник/ Яблонский А.А., Никифорова В.М. – 11-е изд., стер. – СПб.: Лань, 2004. – 768 с. 9 Лекции по теоретической механике: учеб. пособие для втузов/ О.Н. Харин, О.Н. Харин. – М.: РГУ нефти и газа им. И.М. Губкина. – 2004. - Ч.1. – 148 с. 10 Лекции по теоретической механике: учебное пособие для втузов/ О.Н. Харин; О.Н. Харин, авт. Д.Н. Левитский. – М.: РГУ нефти и газа им. И.М. Губкина. – 2004. - Ч.2. – 194 с. 11 Сборник заданий для курсовых работ по теоретической механике/под ред. Яблонского. – М.: Интеграл – Пресс, 2002. 57 СОДЕРЖАНИЕ 1 Указания к выполнению расчетно-графической работы. 1 2 Задание №1.Определение опорных реакций. 2 3 Задание №2.Расчет на прочность ступенчатого бруса круглого сечения на осевое растяжение-сжатие. 14 4 Задание №3.Расчет валов на кручение. 27 5 Задание №4.Расчет на прочность балок при изгибе. 42 6 Задание №5.Расчет вала на изгиб с кручением. 49 7 Список литературы 57 58 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
