реферат. варианты по математике. Указания к выполнению контрольных работ по математике
 Скачать 286.17 Kb. Скачать 286.17 Kb.
|
|
Пример 1.1. Построить многоугольник распределения дискретной случайной величины Х, заданной законом распределения:
Решение:  Рисунок 1.1 – Многоугольник распределения 3 Аналитический, т. е. с помощью формул задается вероятность. Например, формула Бернулли описывает биномиальный закон распределения дискретной случайной величины Х – число появления события (х = k) А в n испытаниях. Рn(k) = 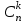 pkqn-k. (1.2) pkqn-k. (1.2)1.1 Числовые характеристики дискретной случайной величины Закон распределения полностью характеризует случайную величину. Но часто закон неизвестен, приходится пользоваться числовыми характеристиками случайных величин. Важной числовой характеристикой является математическое ожидание, которое приближенно равно среднему значению случайной величины. Иногда этого достаточно. Например, математическое ожидание числа выбиваемых очков у 1-ого стрелка лучше, чем у 2-ого стрелка, следовательно, 1-ый стреляет лучше. Математическим ожиданием дискретной величины называют сумму произведений всех ее возможных значений на их вероятности. 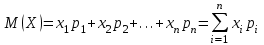 . (1.3) . (1.3)Математическое ожидание примерно равно (тем точнее, чем больше испытаний) среднему арифметическому наблюдаемых значений случайной величины. Математическое ожидание не может полностью характеризовать случайную величину. Зная математическое ожидание, нельзя судить о том, какие возможные значения она может принимать, как они рассеяны вокруг математического ожидания. Например, рассмотрим дискретные случайные величины Х и Y, заданные следующими распределениями:
М(Х) = - 0,010,5 + 0,010,5 = 0; М(Y) = -1000,5 + 1000,5 = 0. Математические ожидания у них одинаковые, но значения Х близко расположены около М(Х), а значения Y далеко расположены от М(Y). Отклонением называется разность между случайной величиной и ее математическим ожиданием (Х – М(Х)). Теорема. Математическое ожидание отклонения равно нулю. М(Х – М(Х)) = 0. (1.4) Так как среднее значение отклонения равно 0, то для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения вычисляют среднее значение квадрата отклонения. Дисперсией (рассеянием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. D(X) = M[(X – M(X))2]. (1.5) Применяя определение математического ожидания, получим формулу для вычисления дисперсии: D(X) = (x1 – M(X))2p1 + (x2 – M(X))2p2 + … + (xn – M(X))2pn. (1.6) Среднеквадратическим отклонением случайной величины Х называется квадратный корень из дисперсии  . (1.7) . (1.7)Дисперсия имеет размерность, равную квадрату размерности случайной величины, а размерность среднеквадратического отклонения совпадает с размерностью случайной величины. Пример 1.2. Найти математическое ожидание М(Х), дисперсию D(X) и среднеквадратическое отклонение (Х) дискретной случайной величины Х, заданной законом распределения:
Решение: М(Х), D(X), (Х) вычисляем по формулам (1.5) – (1.7) соответственно. М(Х) = 20,1 + 30,4 + 100,5 = 6,4; D(X) = (2 – 6,4)20,1 + (3 – 6,4)20,4 + (10 – 6,4)20,5 = 13,04; (Х) = 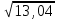 3,61. 3,61.1.2 Функция распределения вероятностей случайной величины Функцией распределения называется функция F(x), определяющая вероятность того, что случайная величина Х в результате испытаний примет значение меньше х, т. е. F(x) = Р( Х х ). (1.8) Другими словами, это вероятность попадания в интервал, расположенный слева от некоторого значения х:  Свойства функции распределения: 1 Так как функции распределения – это вероятность, то ее значения принадлежат отрезку [0, 1], т. е. 0 F(x) 1. 2 F(x) – неубывающая функция, т. е. при x2 x1 F(x2) F(x1). 3 Вероятность того, что случайная величина Х примет значения в интервале (, ), равна приращению функции распределения на этом интервале: Р( Х ) = F() F(). (1.9) 4 Если возможные значения случайной величины принадлежат интервалу (а, b), то F(х) = 0 при х а; F(х) = 1 при х b. График функции распределения расположен в полосе, ограниченной прямыми y = 0, y =1. Пример 1.3. Найти функцию распределения F(х) и построить ее график дискретной случайной величины Х, заданной законом распределения:
Решение: 1 Если х 2, то F(x) = Р( Х 2 ) = 0, так как значений, меньших числа 2 величина Х не принимает. 2 Если 2 х 4, то F(x) = 0,5, так как Х может принимать значение 2 с вероятностью 0,5. 3 Если 4 х 7, то F(x) = 0,7, так как Х может принять значение 2 с вероятностью 0,5 или значение 4 с вероятность 0,2. По теореме сложения вероятностей несовместных событий получаем 0,5 + 0,2 = 0,7. 4 Если х 7, то F(x) = 1, так как событие Х 7 достоверное и его вероятность равна единице. Т  аким образом, функция распределения имеет вид: аким образом, функция распределения имеет вид:График этой функции имеет ступенчатый вид и представлен на рисунке 1.3.  1.3 Непрерывные случайные величины Случайная величина называется непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной. Если возможные значения непрерывной случайной величины расположены на всей оси Х, то 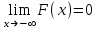 ; ; 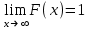 . .Непрерывную случайную величину можно задать, используя другую функции, называемые плотностью распределения. Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(х)– первую производную от функции распределения F(х): f(x) = F(x). (1.10) Отсюда следует, что F(x) – первообразная для f (х). Зная плотность распределения, можно найти функцию распределения: F(x) =  . (1.11) . (1.11)Теорема. Вероятность того, что непрерывная случайная величина Х примет значение из интервала a X b равна определенному интегралу от плотности распределения: P(a X b) = 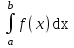 . (1.12) . (1.12)Геометрический смысл. Вероятность того, что непрерывная случайная величина примет значение в интервале (а, b) равна площади криволинейной трапеции, ограниченной осью Ох кривой f (x) и прямыми х = а, х = b. График плотности распределения называется кривой распределения. Свойства плотности распределения: 1 Плотность распределения – неотрицательная функцияf(x) 0, т. е. кривая лежит выше оси Ох или на ней. 2 Несобственный интеграл от плотности распределения от – до + равен единице:  = 1. (1.13) = 1. (1.13)Этот интеграл выражает вероятность события, состоящего в том, что случайная величина Х примет значение из (– ; + ). Это событие достоверное. Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью Ох и кривой f(x) равна единице. Если случайная величина Х принимает значения только в интервале (а, b), то 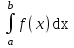 = 1. (1.14) = 1. (1.14)Плотность распределения непрерывной случайной величины называют также законом распределения. 1.4 Нормальное распределение Нормальным называется распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью:  . (1.15) . (1.15)Нормальное распределение задается двумя параметрами: а и , где а – это математическое ожидание, а = М(Х), а – среднеквадратическое отклонение, = (Х). График плотности нормального распределения называется нормальной кривой или кривой Гаусса. Исследуем функцию методами дифференциального исчисления и построим схематично ее график: 1 Область определения – вся ось Ох. 2 f(x) 0, значит график располагается над осью Ох. 3 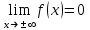 , т.е. ось Ох является горизонтальной асимптотой. , т.е. ось Ох является горизонтальной асимптотой.4 Исследование на экстремум: 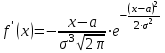  5 Так как (х – а)2 , то график симметричен относительно прямой x = a. 6 Точки перегиба: 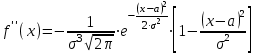 ; ;f (x) = 0 при x = a , при переходе через эти точки f(x) меняет знак.  . . Таким образом, точки перегиба имеют координаты:  . .7 Влияние параметров: изменение параметра а не изменяет формы кривой, а приводит лишь к ее сдвигу вдоль оси Ох: при возрастании а – вправо, при убывании а – влево. С возрастанием maxf(х) убывает, а кривая становится более пологой (прижимается к оси Ох); при убывании кривая становится более острой (растягивается в положительном направлении оси Оу). Но при любых значениях а и площадь, ограниченная нормальной кривой и осью Ох равна единице. Пример 1.4. Математическое ожидание нормально распределенной случайной величины Х равно а = 6 и среднее квадратическое отклонение = 2. Написать плотность вероятности Х построить схематично ее график. Решение. Подставим в формулу (2.27) значения а = 6 и = 2, получим  . Точка максимума: х = 6, fmax (6) = . Точка максимума: х = 6, fmax (6) = 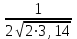 = 0,2. = 0,2.Точки перегиба: х1 = 6 – 2 = 4; х2 = 6 + 2 = 8; fпер. = 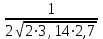 = 0,12. = 0,12.График функции представлен на рисунке 1.4. Вероятность попадания в заданный интервал (; ) непрерывной случайной величины Х определяется по формуле (1.12), при нормальном законе: 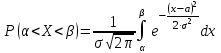 . (1.16) . (1.16) Рисунок 1.4 – График плотности распределения вероятностей нормальной случайной величины Х: а = 6; = 2 После преобразований получаем формулу: 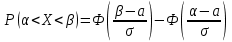 , (1.17) , (1.17)где Ф(х) – интегральная функция Лапласа: 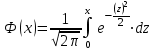 . (1.18) . (1.18)Значения этой функции находятся в таблице 1 приложения, функция нечетная, т. е. Ф(– х) = – Ф(х). Пример 1.5. Пусть непрерывная случайная величина Х изменяется по нормальному закону, а = 30, = 10. Какова вероятность того, что Х принимает значения от 15 до 50 ? Решение: = 15; = 50, подставим в формулу (1.17), получим 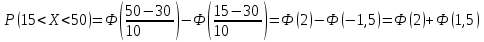 . . По таблице 1 приложения находим: Ф(2) = 0,4772; Ф(1,5) = 0,4332, тогда  . .Ответ: 0,9104. 2 МАТЕМАТИЧЕСКАЯ СТАТИСТИКА 2.1 Основные понятия Математическая статистика занимается изучением закономерностей, которым подчиняются массовые случайные явления, на основе результатов наблюдений. В математической статистике вводятся понятия генеральной и выборочной совокупностей. Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, качественным признаком может служить выполнение нормы спортсменов, а количественным – результат, который показал спортсмен. Провести сплошное обследование, т.е. обследовать каждый из объектов совокупности, на практике часто бывает невозможно хотя бы из-за очень большого числа объектов. В этом случае подвергается обследованию ограниченное число объектов, отобранных случайным образом из всей совокупности объектов. Это так называемый выборочный метод обследования. Генеральной совокупностью называется совокупность всех однородных объектов, подвергающихся изучению. Выборочной совокупностью или просто выборной называется совокупность однородных объектов, случайно отобранных из генеральной совокупности объектов. Объемом совокупности (выборочным или генеральным) называется число объектов этой совокупности и обозначается n. |
