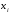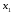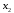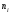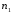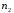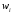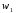реферат. варианты по математике. Указания к выполнению контрольных работ по математике
 Скачать 286.17 Kb. Скачать 286.17 Kb.
|
|
Основной подход в математической статистике по изучению выборочной совокупности устанавливаются свойства всей генеральной совокупности. Поэтому выборка должна достаточно полно характеризовать все особенности генеральной совокупности. Говорят, что выборка должна быть представительной или репрезентативной. Для этого необходимо, чтобы отбор объектов в выборку осуществлялся случайным образом, т.е. все объекты генеральной совокупности должны иметь одинаковую вероятность попасть в выборку. При этом по объему выборка должна быть достаточной, чтобы отмечалась статистическая устойчивость частот наблюдаемых событий. Количественные признаки, характеризующие объекты генеральной совместимости, обозначаются большими буквами Х, Y, Z. Наблюдаемые значения xi называются вариантами, а их последовательность, записанная в возрастающем порядке вариационным рядом. Число наблюдений значения xi называется частотой ni. Относительной частотой называется отношение частоты к объему выборки 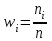 (2.1) (2.1)Пусть из генеральной совокупности извлекается выборка. При этом значение х1 наблюдалось n1 раз, x2 наблюдалось n2 раз и т.д., xk наблюдалось nk раз. Тогда общий объем выборки n = n1 + n2 + … + nk или 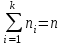 . (2.2) . (2.2)Очевидно, что 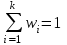 . (2.3) . (2.3)Статистическим распределением выборки называется перечень вариант и соответствующих им частот или относительных частот. Аналогично распределению вероятностей дискретной случайной величины. Табличный вид задания статистического распределения выборки:
Обозначим nx – число наблюдений, при которых наблюдалось значение признака меньше х (X x). Относительная частота события (X x) равна 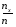 функция от х. Т.к. эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической функцией распределения (статистической): функция от х. Т.к. эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической функцией распределения (статистической):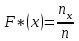 . (2.4) . (2.4)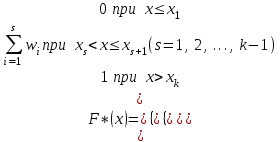 (2.5) (2.5)Эта функция служит для приближенного представления о теоретической функции распределения случайной величины. Аналогично многоугольнику в теории вероятности, в математической статистике строится полигон частот и полигон относительных частот. Полигоном частот называется ломаная прямая, отрезки которой соединяют точки с координатами (х1; n1), (х2; n2), … , (хk; nk). Полигоном относительных частот называется ломаная прямая, отрезки которой соединяют точки (х1; w1), (х2; w2), … , (хk; wk). Пример 2.1. Статистическое распределение выборки задано таблицей:
Составить эмпирическую (статистическую) функцию распределения, построить полигон частот. Объем выборки равен n = 12 + 18 + 30 = 60. Вычислим относительные частоты: w1 =  = 0,2; w2 = = 0,2; w2 = 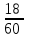 = 0,3; w3 = = 0,3; w3 = 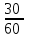 = 0,5; = 0,5;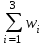 = 0,2 + 0,3 + 0,5 = 1. = 0,2 + 0,3 + 0,5 = 1.
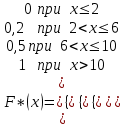 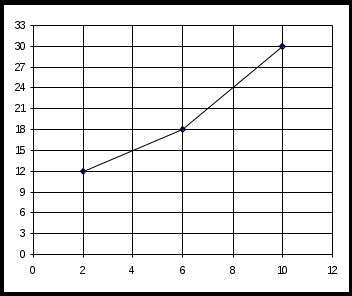  В тех случаях, когда рассматриваемый признак Х является непрерывной случайной величиной, строится не полигон, а гистограмма. Для этого интервал, в который заключены все значения случайной величины, разбивается на несколько частичных интервалов длиной h каждый. На этих интервалах подсчитывается сумма частот вариантni, попавших в каждый интервал, и составляется отношение (ni / h). Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношениям (ni/h) (плотность частот). Гистограммой относительных частот называют фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению (wi / h) (плотность относительных частот). Плотность относительной частоты (wi / h) служит для приближенного представления о плотности распределения вероятностей f (x) генеральной совокупности. Пример 2.2. Построить гистограмму частот по данному распределению выборки объема n = 100, представленному в таблице. Решение. Построим на оси абсцисс заданные частичные интервалы длины h = 4. Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся от нее на расстояниях, равных соответствующим плотностям частот ni / h. Например, над интервалом (1, 5) построим отрезок на высоте n1 / h = 10/4 = 2,5; аналогично строим остальные отрезки. Искомая гистограмма частот изображена на рисунке 2.2.
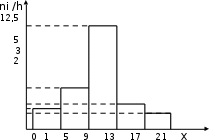 Рисунок 2.2 – Гистограмма частот 2.2 Статистические оценки По виду гистограммы выдвигается гипотеза о законе распределения случайной величины Х генеральной совместимости. Законы распределения характеризуются такими параметрами как математическое ожидание, дисперсия и среднее квадратическое отклонение. Поэтому требуется найти приближенные значения этих параметров по выборочной совокупности, т.е. получить их статистические оценки. По данным выборочной совокупности можно подсчитать выборочную среднюю, выборочную дисперсию и соответствующее среднеквадратическое отклонение. Пусть выборка представлена статистическим распределением:
Выборочная средняя вычисляется по формуле: 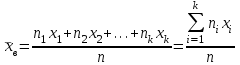 (2.6) (2.6)или 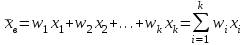 . (2.7) . (2.7)Выборочная дисперсия характеризует рассеивание выборочных данных относительно выборочного среднего: 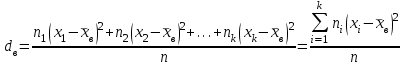 . (2.8) . (2.8)Выборочное среднеквадратическое отклонение: 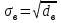 . (2.9) . (2.9)Можно ли выборочную среднюю принять за статистическую оценку математического ожидания генеральной совокупности, выборочную дисперсию за статистическую оценку дисперсии генеральной совокупности, а выборочное среднеквадратического отклонение за оценку среднеквадратического отклонения случайной величины генеральной совокупности? Для того, чтобы статистические оценки давали хорошие приближения оцениваемых характеристик, эти оценки должны удовлетворять требованиям несмещенности, эффективности и состоятельности. Несмещенной, эффективной и состоятельной оценкой математического ожидания M(X) генеральной совокупности является средняя арифметическая выборки, т.е. М(Х) 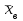 . (2.10) . (2.10)Несмещенной, эффективной и состоятельной оценкой генеральной дисперсии D(X) является исправленная выборочная дисперсия:  = = 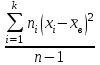 . (2.11) . (2.11)Несмещенной, эффективной и состоятельной оценкой среднеквадратического отклонения генеральной совокупности σ(X) является исправленное выборочное среднеквадратическое отклонение. σ(X) s =  = = 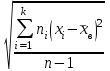 . (2.12) . (2.12)Рассмотренные оценки называются точечными, т.к. определяются одним числом. Пример 2.3. Из генеральной совокупности извлечена выборка объема n = 50:
Найти статистические оценки генеральным средней, дисперсии и среднеквадратического отклонения. Решение. 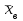 = (162 + 125 + 87 + 1014)/50 = 5,76; = (162 + 125 + 87 + 1014)/50 = 5,76;s2 = ((2 – 5,76)216 + (5 – 5,76)212 + (7 – 5,76)28 + (10 – 5,76)214)/49 = 22,18; s = 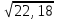 = 4,71. = 4,71.Ответ: 5,76; 22,18; 4,71. ВАРИАНТЫ КОНТРОЛЬНЫХ РАБОТ Контрольная работа «Случайная величина» В таблице представлен закон распределения случайной величины Х. Построить многоугольник распределения, составить функцию распределения F(x) и построить ее график; вычислить числовые характеристики: математическое ожидание М(Х), дисперсию D(Х), среднеквадратическое отклонение (Х) (рекомендация: использовать примеры 1.1; 1.2; 1.3) Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
Вариант 11
Вариант 12
Вариант 13
Вариант 14
Вариант 15
Вариант 16
Вариант 17
Вариант 18
Вариант 19
Вариант 20
23. Ф. Сколько различных шестизначных чисел с неповторяющимися цифрами можно записать с помощью цифр 1; 2 3, 4, 5, 6, если: 1) число должно начинаться с 56; 2) цифры 5 и 6 в числе должны стоять рядом? Решение. Две цифры 5 и 6 фиксируем в начале числа и дописываем к ним различные перестановки из 4 оставшихся цифр; количество различных шестизначных чисел равно: Р4 = 4! = 24. Условно будем считать пару 56 одной цифрой и переставлять ее с четырьмя остальными цифрами; получим Р5 = 5! = 120 различных чисел из 5 цифр, среди которых одна условная, двойная. Если считать условной цифрой пару 65, то получим еще Р5 = 5! = = 120 различных чисел. Общее количество различных шестизначных чисел, в которых цифры 5 и 6 стоят рядом (в любом порядке), равно 120 + 120 = 240 чисел. (Варианты 56 и 65 несовместны, не могут реализоваться одновременно; применяем комбинаторное правило суммы.) Ответ: 1) 24 числа; 2) 240 чисел. 23. Ф. Сколько различных шестизначных чисел с неповторяющимися цифрами можно записать с помощью цифр 1; 2 3, 4, 5, 6, если: 1) число должно начинаться с 56; 2) цифры 5 и 6 в числе должны стоять рядом? Решение. Две цифры 5 и 6 фиксируем в начале числа и дописываем к ним различные перестановки из 4 оставшихся цифр; количество различных шестизначных чисел равно: Р4 = 4! = 24. Условно будем считать пару 56 одной цифрой и переставлять ее с четырьмя остальными цифрами; получим Р5 = 5! = 120 различных чисел из 5 цифр, среди которых одна условная, двойная. Если считать условной цифрой пару 65, то получим еще Р5 = 5! = = 120 различных чисел. Общее количество различных шестизначных чисел, в которых цифры 5 и 6 стоят рядом (в любом порядке), равно 120 + 120 = 240 чисел. (Варианты 56 и 65 несовместны, не могут реализоваться одновременно; применяем комбинаторное правило суммы.) Ответ: 1) 24 числа; 2) 240 чисел. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||