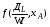ОХТ(шпоры). УКлассификация технологических процессов механические и химические технологии промышленность неорганических веществ промышадность органических веществ (включая производство и переработку пищевых продуктов)
 Скачать 3.28 Mb. Скачать 3.28 Mb.
|
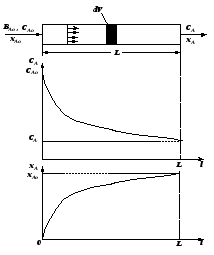
1Реакторы идеального вытесненияРеактор идеального вытеснения (РИВ) представляет собой трубчатый реактор с большим отношением длины трубки L к ее диаметру d (L/d > 20), в который подаются исходные реагенты, превращающиеся по мере перемещения их по длине реактора в продукты реакции (рис.2.4). Гидродинамический режим в РИВ характеризуется тем, что любая частица потока движется только в направлении основного потока в реакторе, обратное перемешивание отсутствует, отсутствует также перенос вещества по сечению, перпендикулярному направлению основного потока (радиальное), т.к. предполагается, что распределение вещества по этому сечению равномерное. Каждый элемент объема реакционной массы dVr движется по длине реактора, не смешиваясь с предыдущими и последующими элементами объема, и ведет себя как поршень в цилиндре, вытесняя все, что находится перед ним. Поэтому, этот режим движения реагентов называют также поршневым, или режимом полного вытеснения.
Состав такого элемента объема последовательно изменяется по длине реактора вследствие протекания химической реакции. Например, концентрация исходного реагента А постепенно изменяется по длине реактора от начального значения CAo до конечного – CA (рис.2.4.). Следствием такого режима движения реакционной смеси является то, что время пребывания каждой частицы в реакторе одно и то же. Для получения характеристического уравнения РИВ исходят из дифференциального уравнения материального баланса (1.8), упрощая его на основе указанных выше особенностей этого реактора. Поскольку в РИВ реакционная смесь движется только в одном направлении (по длине l), то для первой группы членов правой части уравнения (1.8) можно записать (выбрав за направление оси Х направление движения потока реагентов в реакторе):
Так как каждый элемент объема реакционной смеси в реакторе не смешивается ни с предыдущими, ни с последующими объемами, а также отсутствует радиальное перемешивание, т.е. нет ни продольной, ни радиальной диффузии, то:
С учетом вышесказанного, уравнение (1.8) для реактора идеального вытеснения принимает вид:
Это уравнение материального баланса является математическим описанием потока реагента в реакторе идеального вытеснения при нестационарном режиме (таком, когда параметры процессе меняются не только по длине реактора, но и непостоянны во времени). Такой режим характерен для периода пуска и остановки реактора. Член 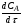 характеризует изменение концентрации во времени для данной точки реактора – это накопление вещества А в этой точке. Из уравнения (2.25) видно, что накопление зависит от конвективного переноса вещества в данной точке реактора характеризует изменение концентрации во времени для данной точки реактора – это накопление вещества А в этой точке. Из уравнения (2.25) видно, что накопление зависит от конвективного переноса вещества в данной точке реактора 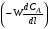 и от расхода вещества на химическую реакцию (rA). и от расхода вещества на химическую реакцию (rA).Стационарный режим характеризуется тем, что параметры в данной точке реакционного объема не меняются во времени, т.е. 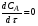 . Тогда уравнение (2.25) принимает вид: . Тогда уравнение (2.25) принимает вид:
Из уравнения (2.26) видно, что при стационарном режиме изменение массового потока вещества А в данной точке реакторе равно скорости расходования А по химической реакции. Из уравнения (2.26) легко получить характеристическое уравнение РИВ. Если объем реакционной смеси не изменяется в процессе, то справедливо уравнение (2.7):
после дифференцирования которого получаем
Длину пути можно выразить так:
Откуда при постоянной скорости потока
Подставив полученное значение для dCA и dl в уравнение (2.26), находим:
После интегрирования уравнения (2.30) в пределах изменения степени превращения от 0 до xA получаем характеристическое уравнение РИВ:
Уравнение (2.31) для РИВ аналогично уравнению (2.10), полученному для РИС-периодического. В уравнении (2.10) время – есть время проведения реакции в периодическом реакторе (от загрузки сырья до выгрузки продуктов), а в уравнении (2.31) – время, в течение которого реакционная смесь проходит через РИВ от входа в реактор до выхода из него (при условии, что реакция идет без изменения объема).
Уравнение (2.31) для необратимой реакции n-го порядка принимает вид:
или с учетом уравнения (2.7)
Для реакции нулевого порядка
Для необратимой реакции первого порядка
Для реакций более высоких порядков целесообразно для определения времени пребывания использовать метод графического интегрирования. Для этого строят графическую зависимость 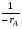 от xA (рис. 2.5) и вычисляют площадь под кривой Sвыт между начальным и конечным значениями степени превращения xA0 и xA: от xA (рис. 2.5) и вычисляют площадь под кривой Sвыт между начальным и конечным значениями степени превращения xA0 и xA:
До сих пор речь шла о реакциях, идущих без изменения объема. Если же реакция идет с изменением объема, то необходимо учитывать, что концентрация вещества А изменяется не только за счет химического превращения, но и за счет изменения объема реакционной смеси и, текущая концентрация А не может быть рассчитана по уравнению (2.7). Изменение объема реакционной смеси учитывают с помощью коэффициента относительного изменения объема:
В частном случае, при линейном изменении объема реакционной смеси V от степени превращения, можно записать
При подстановке значения V из уравнения (2.38) в уравнение (2.6)
получаем уравнение для расчета текущей концентрации CA при степени превращения xA с учетом изменения объема реакционной смеси:
Изменение объема реакционной смеси в зависимости от степени превращения xA учитывают и при выходе характеристических уравнений реакторов. Так, например, характеристическое уравнение реактора идеального вытеснения (2.31) с учетом уравнения (2.39) записывается для реакции n-го порядка в виде:
В реальных реакторах вытеснения гидродинамическая обстановка отличается от обстановки в идеальном реакторе (РИВ). В реальном трубчатом реакторе наряду с переносом вещества А в направлении движения потока реакционной массы возможно обратное перемешивание вещества А вдоль оси реактора в направлении, противоположном движению потока (обратная диффузия), а также перемещение вещества А в радиальном направлении (радиальная диффузия). Модель, отражающая гидродинамическую обстановку в реальном реакторе, где имеется только обратное перемешивание, называется однопараметрической диффузионной моделью. Модель, учитывающая наряду с обратным перемешиванием и радиальное, называется двухпараметрической диффузионной моделью. Исходным уравнением для вывода диффузионной модели является (как и для РИС-П и РИВ) дифференциальное уравнение материального баланса (1.8). Принимая во внимание, что ось Х направлена вдоль длины реактора, как и для реактора идеального вытеснения здесь справедливы равенства (2.23):
Но в отличие от реактора идеального вытеснения, не все члены уравнения (1.8), отражающие перенос вещества диффузией, равны нулю. Для однопараметрической диффузионной модели:
С учетом этого уравнение (1.8) принимает вид:
Это однопараметрическая диффузионная модель для нестационарного режима. При стационарном режиме 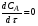 , и уравнение (2.42) можно записать: , и уравнение (2.42) можно записать:
Из уравнения (2.43) видно, что условием стационарности в этом случае является равенство скорости переноса вещества А потоком и диффузией и скорости превращения вещества А по химической реакции. Рассуждая аналогичным образом, можно получить из уравнения (1.8) и двухпараметрическую диффузионную модель, которая имеет вид (для нестационарного режима):
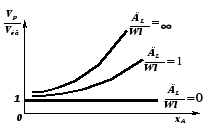
Степень отклонения реального реактора от идеального зависит от ряда показателей: для однопараметрической модели – от коэффициента продольного перемешивания (турбулентной диффузии) ДL, линейной скорости потока W и длины реактора L. Эти показатели сведены в безразмерный комплекс 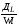 , представляющий собой обратный критерий Пекле , представляющий собой обратный критерий Пекле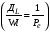 . .Степень отклонения, зависящая от комплекса 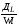 , может быть установлена сравнением объемов идеального реактора Vид и реального реактора Vp, необходимых для достижения одинаковой степени превращения xA, что может быть изображено графически (рис. 2.6), где на оси абсцисс отложена xA, а на оси ординат отношение Vp/Vид. , может быть установлена сравнением объемов идеального реактора Vид и реального реактора Vp, необходимых для достижения одинаковой степени превращения xA, что может быть изображено графически (рис. 2.6), где на оси абсцисс отложена xA, а на оси ординат отношение Vp/Vид.Чем больше комплекс 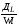 , тем больше отклонение гидродинамического режима в реальном реакторе от режима в идеальном реакторе и тем больше отношение Vp/Vид. При , тем больше отклонение гидродинамического режима в реальном реакторе от режима в идеальном реакторе и тем больше отношение Vp/Vид. При 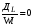 имеем режим идеального вытеснения, поэтому Vp/Vид = 1 и необходимый объем реального реактора Vp = Vид. имеем режим идеального вытеснения, поэтому Vp/Vид = 1 и необходимый объем реального реактора Vp = Vид.Если 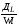 >0 , то Vp/Vид > 1 и чем больше, тем больше >0 , то Vp/Vид > 1 и чем больше, тем больше 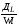 необходимый объем реального реактора по сравнению с объемом идеального реактора. Особенно сильно проявляется различие в объеме реакторов при больших степенях превращения xA (см. рис. 2.6). необходимый объем реального реактора по сравнению с объемом идеального реактора. Особенно сильно проявляется различие в объеме реакторов при больших степенях превращения xA (см. рис. 2.6).
Таким образом:
Все это необходимо принимать во внимание при расчете реального реактора. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

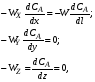
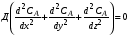
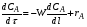
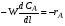
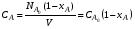 ,
,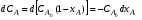
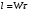 ,
,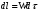
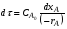
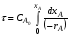
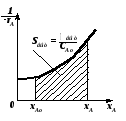

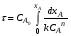
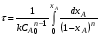
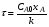
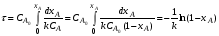
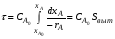
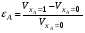 ,
,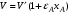
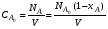
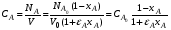
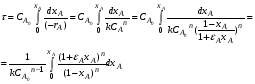
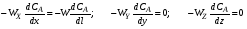
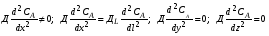 ,
,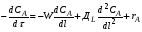
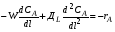
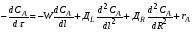 ,
,
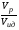 =
=