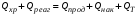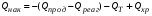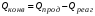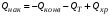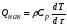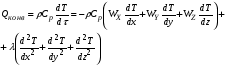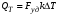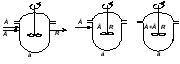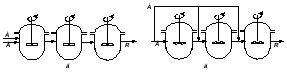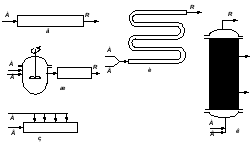ОХТ(шпоры). УКлассификация технологических процессов механические и химические технологии промышленность неорганических веществ промышадность органических веществ (включая производство и переработку пищевых продуктов)
 Скачать 3.28 Mb. Скачать 3.28 Mb.
|
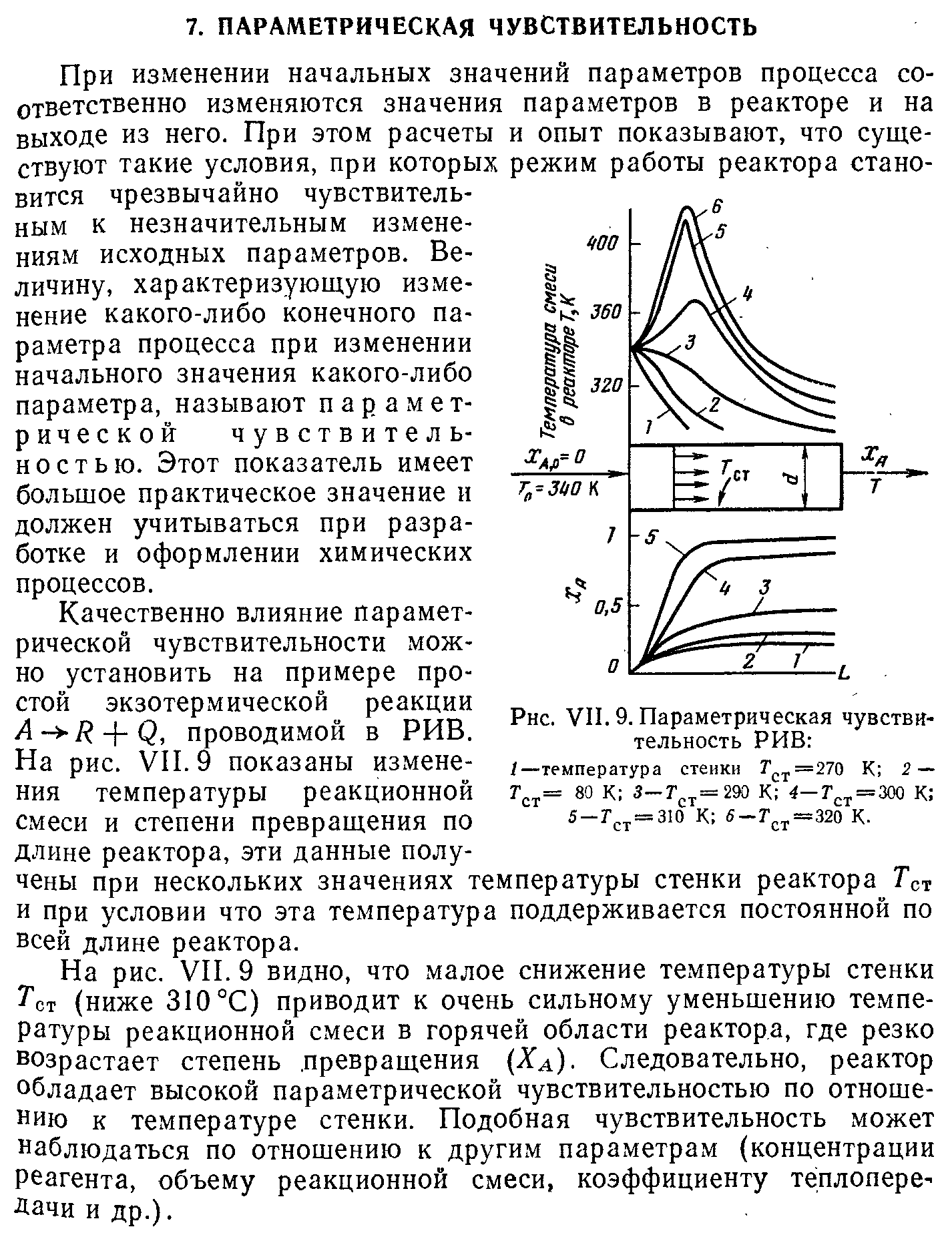
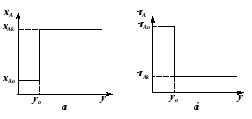
2 Реакторы идеального смешения непрерывного действияНепрерывный реактор идеального смешения (РИС-Н) – это реактор с мешалкой, в который непрерывно подают реагенты и выводят из него продукты реакции (рис. 2.7). Благодаря интенсивному перемешиванию потоков мгновенно устанавливается одинаковая по всему объему реактора концентрация реагента CA, равная его концентрации на выходе из реактора (рис. 2.7). Резкое изменение концентрации при выходе реагентов в реактор происходит за счет мгновенного смешения поступающих реагентов с реакционной массой, уже имеющейся в реакторе, где концентрация компонента А значительно ниже, чем в подаваемой реакционной смеси.
Величина перепада между начальной CAo и конечной концентрацией CA исходного реагента зависит при прочих условиях от величины скорости химической реакции. Чем она выше, тем меньше концентрация реагента А в реакторе и больше перепад CAo – CA. С другой стороны, при одной и той же скорости реакции величина перепада зависит от времени пребывания реагентов в реакторе, . Чем больше , тем полнее проходит реакция, и тем ниже концентрация реагента, CA, в реакционной смеси (рис. 2.8). Точка, соответствующая входу реагентов в реактор, нанесена на оси абсцисс правее начала координат, что дает более наглядное представление об изменении концентрации при входе реакционной смеси в реактор.
Так как концентрация реагентов в проточном реакторе идеального смешения одинакова во всех точках реакционного объема, то постоянны по объему и другие параметры – степень превращения и скорость реакции (рис 2.9). Поэтому материальный баланс по какому-либо компоненту, необходимый для получения характеристического уравнения, составляют в конечных величинах (по разности концентраций реагента на входе в реактор и выходе из него), то есть используют уравнение (1.7):
Из уравнения (2.46) видно, что условием стационарности процесса является равенство скорости конвективного переноса вещества А и скорости его химического превращения.
При стационарном режиме ВАнак.= 0, и
Найдем значения величин, входящих в уравнение (2.46). Так по уравнению (1.6)
Подставляя (2.47-2.49) в (2.46), получаем:
или, учитывая, что ВAo = CAoV, где V – объемный расход реагентов, имеем:
Отношение Vr/V – это условное время пребывания, (см. уравнение (2.17)). Тогда
Это характеристическое уравнение реактора идеального смешения. Для более общего случая, когда начальная степень превращения xAo не равна нулю, оно записывается
Для простой необратимой реакции n-го порядка с учетом уравнения (2.7) уравнение (2.52) принимает вид:
Реактор идеального смешения непрерывного действия (РИС-Н). Для реакции нулевого порядка: CA0xA=CA0-CA
Для реакции первого порядка
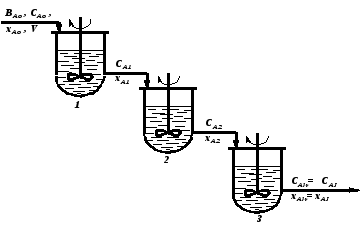
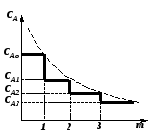
Единичный реактор идеального смешения не дает высокой степени превращения, так как концентрация исходных реагентов в нем мгновенно падает до конечного значения. Поэтому применяют ряд последовательно расположенных непрерывных реакторов смешения – каскад реакторов – К-РИС (рис. 2.15). Концентрация CА в такой системе падает до конечного значения не сразу, а постепенно, от реактора к реактору (рис. 2.16). В каждом реакторе концентрация компонента в объеме постоянна и равна концентрации на выходе из реактора. Изменение концентрации в реакторах происходит мгновенно скачком при входе реакционной смеси в реактор. Рабочая концентрация CA в каскаде реакторов в общем выше, чем в единичном реакторе смешения и приближается с увеличением числа реакторов к значению ее в реакторе вытеснения. Чем больше степеней изменения концентрации в каскаде m (чем больше реакторов), тем больше каскад реакторов приближается к реактору идеального вытеснения (рис.2.16). Выдача расчета каскада реакторов заключается в определении числа ступеней (числа реакторов) – m, необходимых для достижения заданной степени превращения xA.
Существуют аналитический и графический методы расчета каскада реакторов. Аналитический метод выгодно применять при протекании реакции первого порядка, а для реакций более высоких порядков удобнее второй – графический метод.
Для расчета каскада реакторов необходимо: 1) иметь сведения о кинетике процесса [-rA = f(CA)], 2) знать концентрацию исходного реагента А на входе в первый реактор, CAo, и на выходе из последнего реактора, CAm, то есть общую степень превращения xA, 3) задаться объемом единичного реактора (то есть временем пребывания в единичном реакторе смешения, см), при этом предполагают, что объемы единичных реакторов в каскаде равны. Для единичного m-го реактора идеального смешения, исходя из уравнения (2.52), имеем:
Из уравнения (2.70) можно найти скорость процесса в реакторе. Для этого представим его в таком виде:
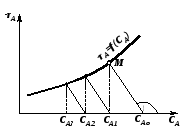
Концентрация реагента на входе в реактор, CAm-1, и время пребывания, см, – величины известные и постоянные, так как даются по условию. Таким образом, из уравнения (2.71) следует, что скорость реакции (- rA) линейно зависит только от концентрации на выходе, CAm. Если эту зависимость выразить графически, то прямая, описываемая уравнением (2.71), пересекает ось абсцисс в точке СAm-1 и имеет тангенс угла наклона , равный 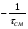 (рис.2.17). Для нахождения концентрации в m-ом реакторе необходимо уравнение (2.71) решить совместно с кинетическим уравнением (2.11), то есть: (рис.2.17). Для нахождения концентрации в m-ом реакторе необходимо уравнение (2.71) решить совместно с кинетическим уравнением (2.11), то есть:
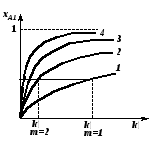
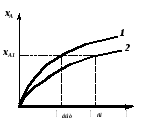
Поэтому, для нахождения концентрации реагента на выходе из первого реактора, CA1, необходимо из точки CAo, лежащей на оси абсцисс, провести прямую с тангенсом наклона 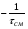 до пересечения с кривой -rA=f(CA) в точке М. до пересечения с кривой -rA=f(CA) в точке М.Если опустить перпендикуляр из точки пересечения прямой и кривой (точка М, см. рис. 2.17), то на оси абсцисс можно получить значение концентрации CA1 в первом реакторе. Эта же концентрация является входной для второго реактора. Для нахождения концентрации во втором реакторе CA2 операция повторяется из точки CA1. Такие операции продолжают повторять до тех пор, пока в последнем реакторе не будет достигнута заданная конечная концентрация CAк. Так как время пребывания во всех реакторах одинаково, то постоянен угол наклона прямых и, следовательно, они параллельны. Число ступеней изменения концентрации и будет числом реакторов в каскаде, необходимым для достижения заданной степени превращения xAк. Как было показано ранее, с увеличением числа реакторов в каскаде характер изменения параметров в нем приближается к реактору идеального вытеснения. Поэтому при увеличении числа реакторов в системе будут сильнее проявляться все свойства, присущие реактору идеального вытеснения, и наоборот. В качестве примера на рисунке 2.18 приведена зависимость степени превращения от величины k (где k – константа скорости реакции) для реакции первого порядка в каскаде с различным числом реакторов m; произведение k характеризует общий объем системы.
Из рисунка 2.18 видно, что при одинаковом объеме каскада (k) степень превращения xA повышается с увеличением числа реакторов в каскаде, приближаясь к степени превращения, получаемой в реакторе идеального вытеснения ( при m ). Если же сравнить каскады, где получена одна и та же степень превращения xA, то общий объем системы будет меньше там, где взято большее число реакторов [(k)2 < (k)1] (рис.2.18). Меняя число реакторов в каскаде, можно влиять не только на степень превращения xA, но и на селективность процесса и выход целевого продукта (для сложной реакции). При этом необходимо учитывать, что с уменьшением числа реакторов каскад будет давать эффект, близкий к эффекту в реакторе смешения, а с увеличением числа ступеней в системе характер связи между степенью превращения, селективностью и выходом целевого продукта становится таким, как и в реакторе вытеснения.
В полунепрерывных реакторах одна из вспомогательных операций – загрузка реагентов или выгрузка продуктов реакции – осуществляется периодически, а вторая операция – непрерывно. Примером такого реактора может служить доменная печь, в которую загрузка твердой шихты проводится непрерывно, а готовый жидкий продукт (чугун) выпускается из домны периодически. В печи разложения СаСО3 с получением СаО и СО2, наоборот, – шихта (уголь и СаСО3) загружается периодически, а продукты реакции (СаО и СаО2) выводятся непрерывно. Так же осуществляется процесс в газогенераторах – уголь (шихта) загружается периодически, а продукт реакции – генеральный газ – выводится непрерывно
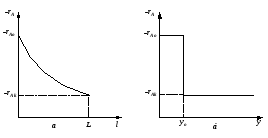
Характеристические уравнения для РИС-П и РИВ одинаковые (2.10) и (2.31), поэтому время для достижения заданной степени превращения в этих реакторах одно и то же. Но в РИС-П полное время процесса складывается из вспомогательного времени и рабочего времени (уравнение 2.2), а в РИВ вспомогательных операций нет, процесс протекает непрерывно, поэтому интенсивность в РИВ выше, чем в РИС-П. В РИС-Н вспомогательные операции также отсутствуют, но гидродинамическая обстановка в нем отличается от обстановки, наблюдаемой в РИВ, поэтому в одинаковых по объему реакторах достигается при прочих равных условиях разная степень превращения исходных компонентов. В связи с этим приведем некоторые сравнительные данные по этим реакторам. Важнейшими факторами, определяющими экономичность процесса, являются размер реактора ( то есть его интенсивность), избирательность процесса, то есть селективность и выход продукта. Для простых реакций имеет значение только первый фактор, то есть размер реактора, необходимый для достижения заданной степени превращения xA, поэтому рассмотрим вначале этот более простой случай. В реакторе вытеснения наблюдается постепенное изменение концентрации по длине реактора, а в реакторе смешения – резкое падение концентрации до конечного значения CA (рис. 2.10). Такой же характер (рис. 2.11) имеет для этих реакторов изменение скоростей реакции (при постоянной температуре).
Из рисунка 2.11. видно, что средняя скорость реакции в реакторе идеального смешения всегда ниже, чем в реакторе вытеснения.
Для необратимых реакций, порядок которых n=0, это не оказывает влияния на интенсивность процесса (для таких реакций скорость не зависит от концентрации реагента) и на выбор типа реактора, что и следует из уравнений (2.14) и (2.55). Таким образом
Для реакций, порядок которых n>0, тип реактора имеет важное значение, так как для достижения одинаковой степени превращения в реакторе смешения нужно большее время, чем в реакторе вытеснения (см >выт) и, следовательно, его интенсивность ниже. Для необратимых реакций первого порядка это можно показать, исходя из уравнений (2.17) и (2.56):
из которых следует, что см>выт, поскольку при изменении xA от 0 до1:
Неравенство (2.58) тем значительнее, чем больше xA (рис. 2.12).
Сопоставление характеристик реакторов для реакции любого и особенно высокого порядка часто отражают графически. Для реактора вытеснения время выт, необходимое для достижения заданной степени превращения xA, выражается уравнением (2.36)
Для реактора смешения см выражается уравнением:
Из уравнений (2.36) и (2.59) следует, что отношение площадей Sсм и Sвыт равно отношению условных времен пребывания реагентов в реакторах смешения и вытеснения (то есть объемов реакторов):
Для сложных реакций судить об эффективности реактора по его размерам (по степени превращения) недостаточно. Для сложных реакций реактор должен еще обеспечивать и необходимую селективность процесса. Для реакций, селективность которых зависит от концентрации реагента (когда порядки основной и побочной реакций различны), на селективность можно повлиять, выбирая определенный тип реактора. Например, для параллельных необратимых реакций:
Селективность 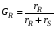 зависит от отношения скоростей образования целевого продукта rR и побочного rS , то есть зависит от отношения скоростей образования целевого продукта rR и побочного rS , то есть 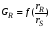 . .Значения rRи rS определяются по уравнениям:
Следовательно:
Из уравнения (2.65) видно, что для каждого конкретного случая, когда известен порядок основной и побочной реакции, селективность зависит только от концентрации CA, так как отношение констант скорости реакций k1/k2 при постоянной температуре величина постоянная. Если порядок основной реакции выше порядка побочной реакции (n1 – n2>0), то для получения высокой селективности (большого отношения 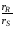 ) необходимо поддерживать концентрацию реагента А на максимальном уровне. Следовательно, для этого следует применять реактор вытеснения, так как средняя текущая концентрация CA в нем выше, чем в реакторе смешения. ) необходимо поддерживать концентрацию реагента А на максимальном уровне. Следовательно, для этого следует применять реактор вытеснения, так как средняя текущая концентрация CA в нем выше, чем в реакторе смешения.Когда же порядок основной реакции ниже порядка побочной реакции (n1-n2<0), в реакторе необходимо поддерживать минимальную концентрацию реагента А, то есть предпочтителен реактор смешения. Когда n1 = n2, то
Следовательно, в этом случае тип реактора не влияет на селективность, и ее можно изменять, меняя соотношение констант скоростей, а для этого нужно применять катализатор селективного действия, либо изменять температуру, так как по Аррениусу:
Поскольку два основных требования – наименьший размер реактора и селективность – являются часто взаимоисключающими факторами, расчет должен быть направлен на удовлетворение одного из требований. На вопрос, какое из требований целесообразнее удовлетворить, можно ответить после проведения технико-экономического анализа. В том случае, когда n1 – n2<0, то есть когда селективность увеличивается с понижением концентрации CA, целесообразно доя повышения селективности применять реактор смешения. Однако применение реактора смешения обычно влечет за собой увеличение его объема. В связи с этим оптимальные условия процесса можно найти сопоставлением затрат на очистку конечной смеси от побочного продукта (низкая селективность) и на увеличение стоимости реактора и его обслуживания при увеличении его размеров. От типа реактора могут зависеть не только степень превращения исходных реагентов и селективность процесса, но и выход целевого продукта. Выход ФR определяется по уравнению
Выбор реактора производится комплексно с учетом связи между xA, GR и ФR. Для реактора идеального смешения связь между приведенными параметрами для необратимой реакции:
описывается соотношением:
Для РИВ степень превращения xA и селективность GR меняются по длине реактора, поэтому для реактора вытеснения:
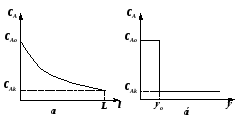
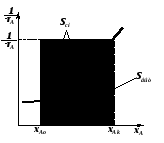
Графическое представление зависимости селективности GR от степени превращения xA позволяет непосредственно выбрать оптимальную модель реактора для достижения максимального выхода ФR. Согласно соотношениям (2.68) и (2.69) выход ФR, достигаемый в реакторе идеального вытеснения, представляется на графике площадью под кривой между значениями xAo и xA (рис. 2.14), выход же в реакторе смешения – площадью прямоугольника со сторонами, равными xA – xAo и GR.
Если селективность уменьшается с ростом степени превращения (когда n1 – n2 >0), то есть при снижении CA (рис. 2.14a), для получения большого выхода ФR необходим реактор вытеснения, так как площадь под кривой для этого реактора будет больше Sвыт>Sсм. Если селективность увеличивается с ростом xA (когда n1 – n2<0), то большой выход достигается в реакторе идеального смешения, для него Sсм>Sвыт (рис. 2.14б).
 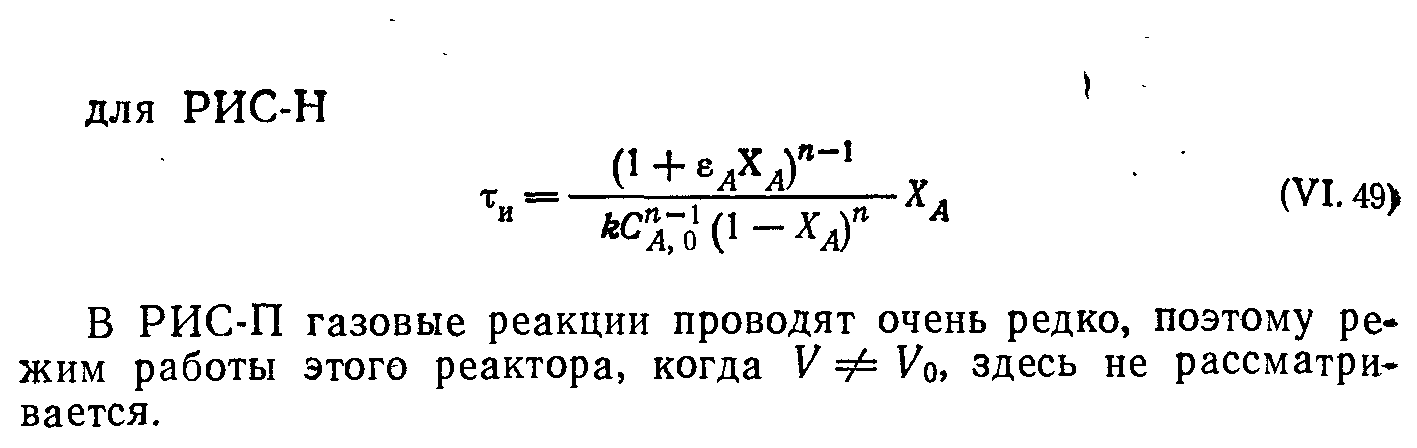
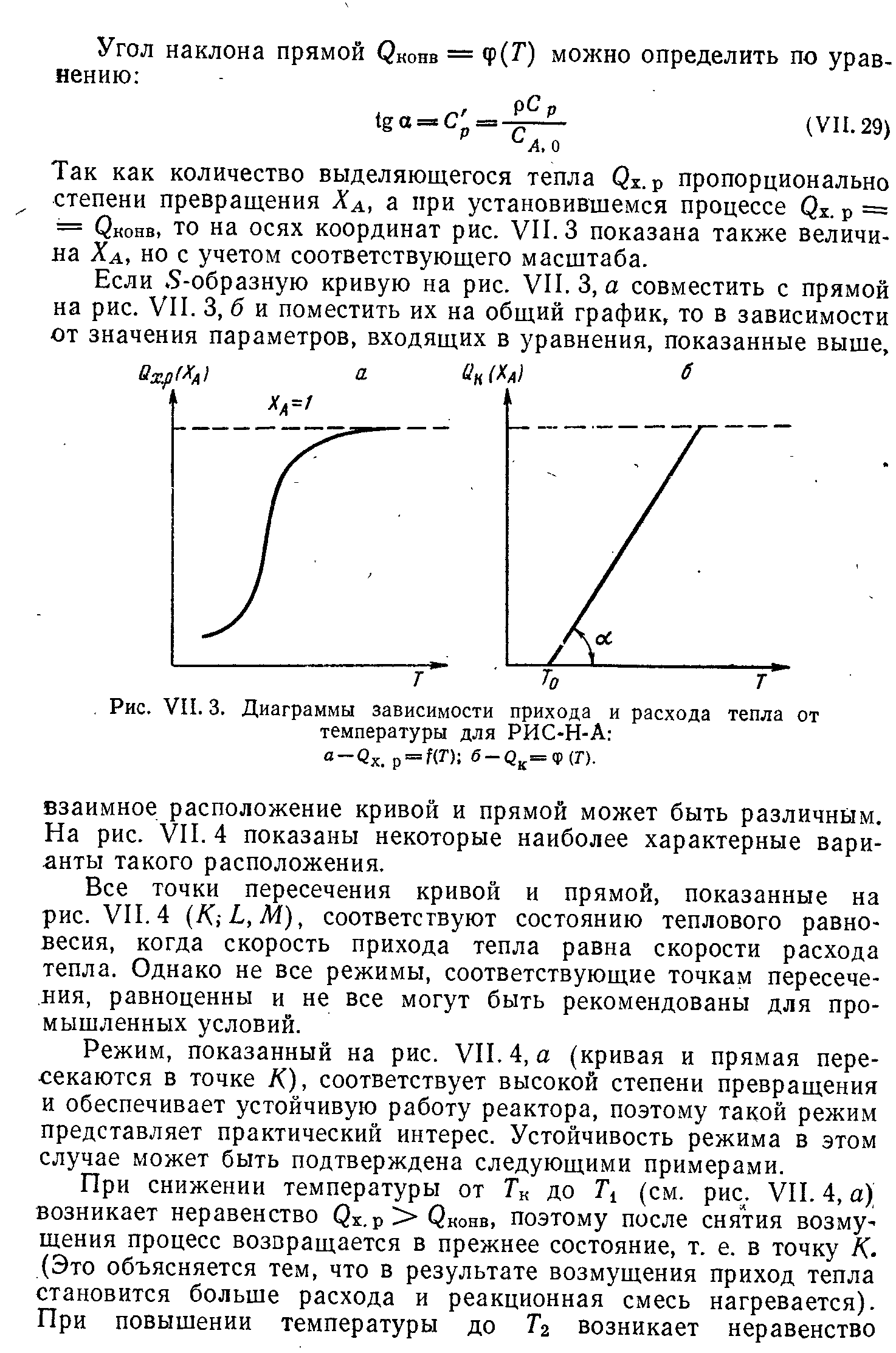
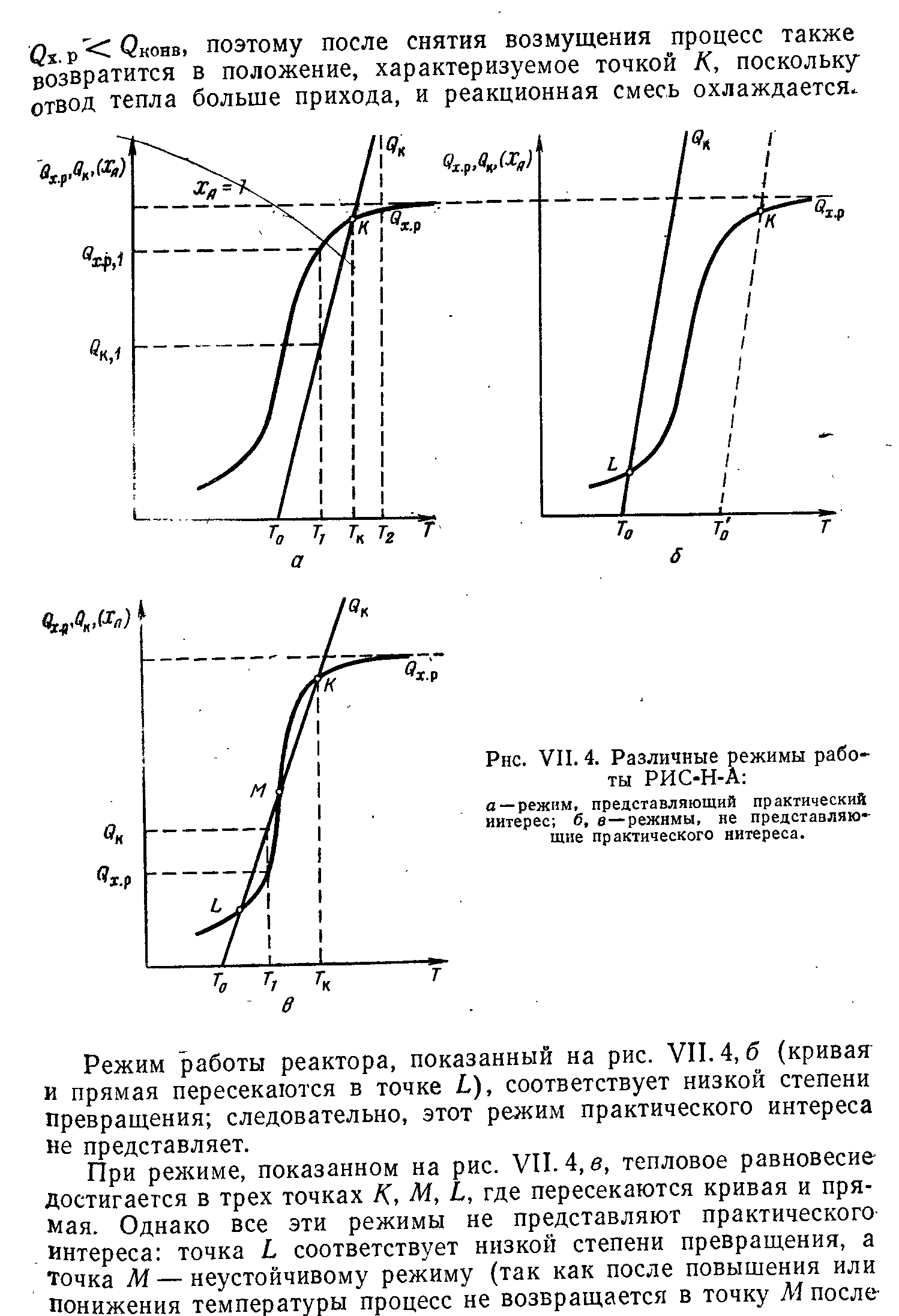
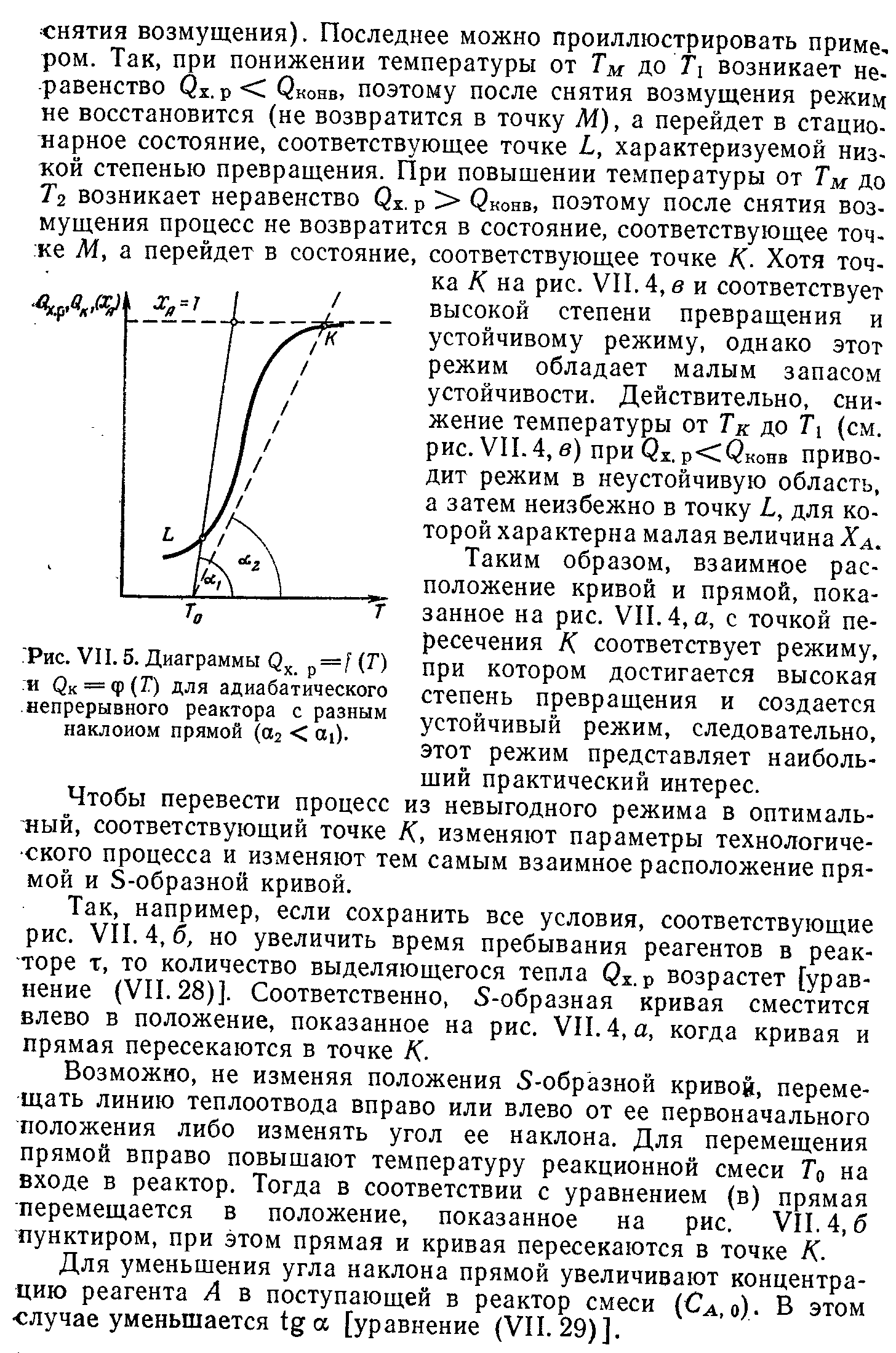
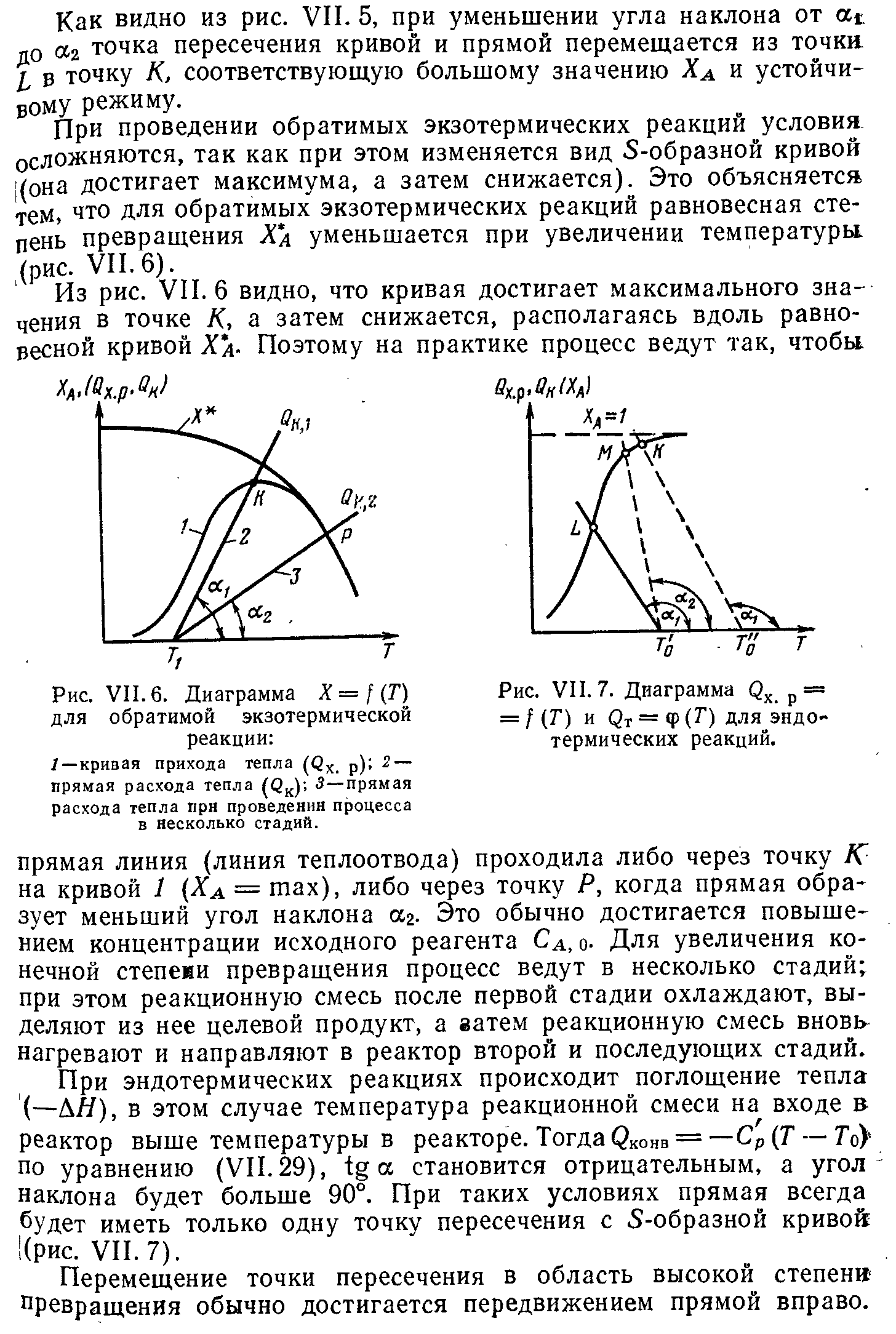
В зависимости от теплового режима реакторы разделяются на три группы: адиабатические, изотермические и политропические. В адиабатическом реакторе отсутствует теплообмен с окружающей средой, и тепло химической реакции полностью расходуется на изменение температуры реакционной смеси. В изотермическом реакторе путем подвода или отвода тепла поддерживают постоянную температуру в течение всего процесса. В политропическом реакторе температура не постоянна, при этом часть тепла отводится или подводится. Адиабатический и изотермический реакторы представляют предельные случаи, которых на практике не бывает, но режим многих реакторов приближается к этим крайним моделям, поэтому с достаточной для практических целей точностью реакторы могут рассчитываться по уравнениям, полученным для адиабатических и изотермических режимов. Исходным уравнением для расчета реакторов с учетом переноса тепла уравнение теплового баланса, которое обычно составляют по одному из компонентов реакционной смеси.
Тепловой баланс в общем виде можно представить уравнением:
Рассмотрим случай, когда простая необратимая реакция (1.2) протекает с выделением тепла, т.е.:
Тогда приход тепла можно записать в виде:
Расход тепла может быть представлен уравнением:
Подставив значения Qприх и Qрасх (3.3 и 3.4) в уравнение, получаем:
После перестановки членов уравнения (3.5) может быть записано в таком виде:
Разность между теплом, уносимым из реактора нагретыми продуктами реакции и теплом, вносимым в реактор исходными реагентами, представляет конвективный поток тепла:
С учетом выражения (3.7) уравнение (3.6) примет вид:
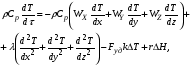
Уравнение теплового баланса (3.8) может принимать различную форму в зависимости от типа реактора и теплового режима процесса. В общем случае имеет место изменение параметров процесса (температура, концентрация и др.) по объему реактора или по времени, в связи с чем тепловой баланс (так же, как и материальный) составляют в дифференциальной форме. Для этой цели используют дифференциальное уравнение конвективного теплообмена (А.Г. Касаткин, Основные процессы и аппараты в химической технологии, 1971, стр. 294), в которое вводят дополнительные члены, учитывающие отвод тепла в результате теплообмена) и тепло реакции; с такими дополнениями уравнение имеет вид:
Группа членов левой части уравнения (3.9) выражает скорость накопления тепла в элементарном объеме, для которого составляется тепловой баланс. Этому члену соответствует величина Qнак, уравнение (3.8), т.е.:
Первая группа членов первой части уравнения (3.9) отражает конвективный перенос тепла по соответствующим координатам (x, y, z) в элементарном объеме. Вторая группа членов правой части уравнения (3.9) отражает изменение тепла, связанное с теплопроводностью реакционной среды (). Суммарному переносу тепла конвективным потоком, отражаюшим влияние теплопроводности (обратная диффузия), соответствует в уравнении (3.8) член Qконв, в результате чего можно записать:
Из сравнения уравнений (3.8) и (3.9) далее следует:
Решение уравнения (3.9) часто связано с большими трудностями. Однако, как будет показано ниже, в зависимости от характера протекающей реакции, гидродинамического и теплового режимов в реакторе, значение отдельных членов уравнения становится пренебрежительно мало, что приводит к более простым уравнениям, обеспечивающим достаточно точные решения самых разнообразных практических задач. Уравнения (3.8) и (3.9) представляют математическое описание потоков тепла в нестационарном режиме, когда имеет место накопление тепла и температура процесса меняется во времени. Для реакторов непрерывного действия характерен стационарный режим. Неустановившееся состояние наблюдается только в пусковой период и в период остановки реактора. В дальнейшем все реакторы непрерывного действия будут рассматриваться только в стационарном режиме, когда отсутствует накопление тепла, т.е. Qнак = 0. В реакторах периодического действия режим всегда нестационарный: происходит накопление тепла в результате химического превращения, и температура в любой точке реактора меняется во времени, т.е. Qнак 0. С другой стороны, в реакторах периодического действия отсутствует конвективный перенос тепла и член Qконв= 0. Из приведенных примеров следует, что для описания конкретных типов реакторов уравнения (3.8) и (3.9) приобретут более простой вид. Форма уравнения теплового баланса определяется также тепловым режимом в реакторе, что будет показано в дальнейшем. Ниже даются выводы уравнений тепловых балансов и способы их решения для различных типов реакторов, работающих в различных тепловых режимах.


  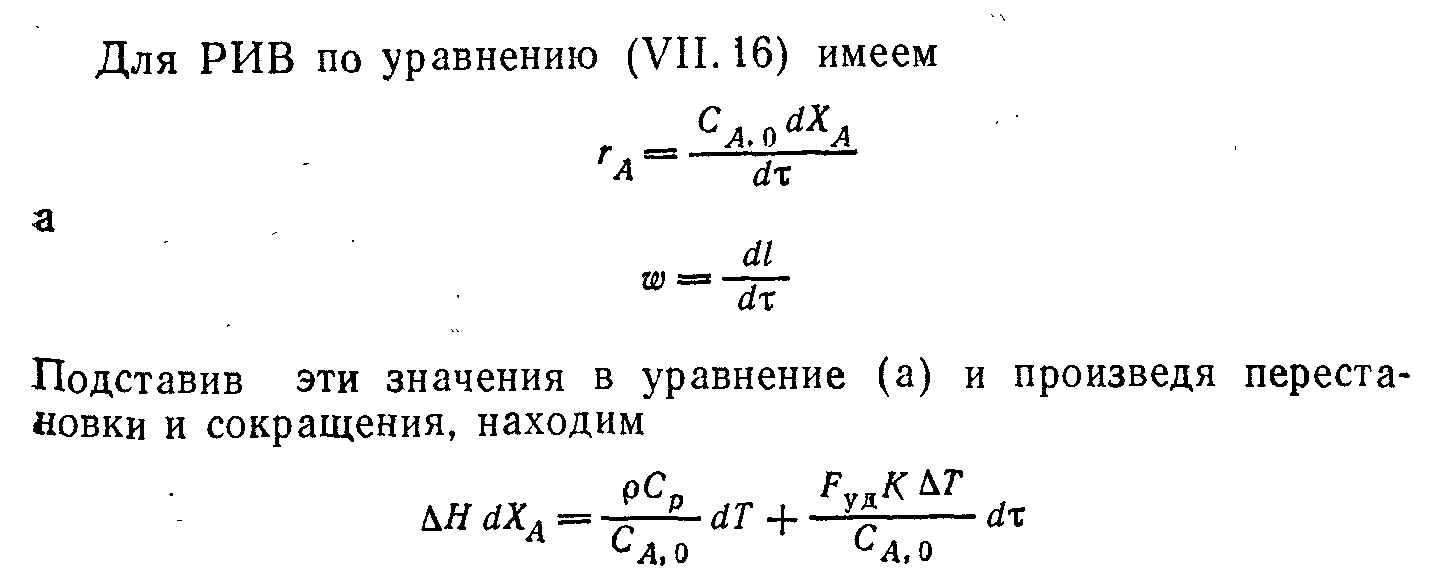 
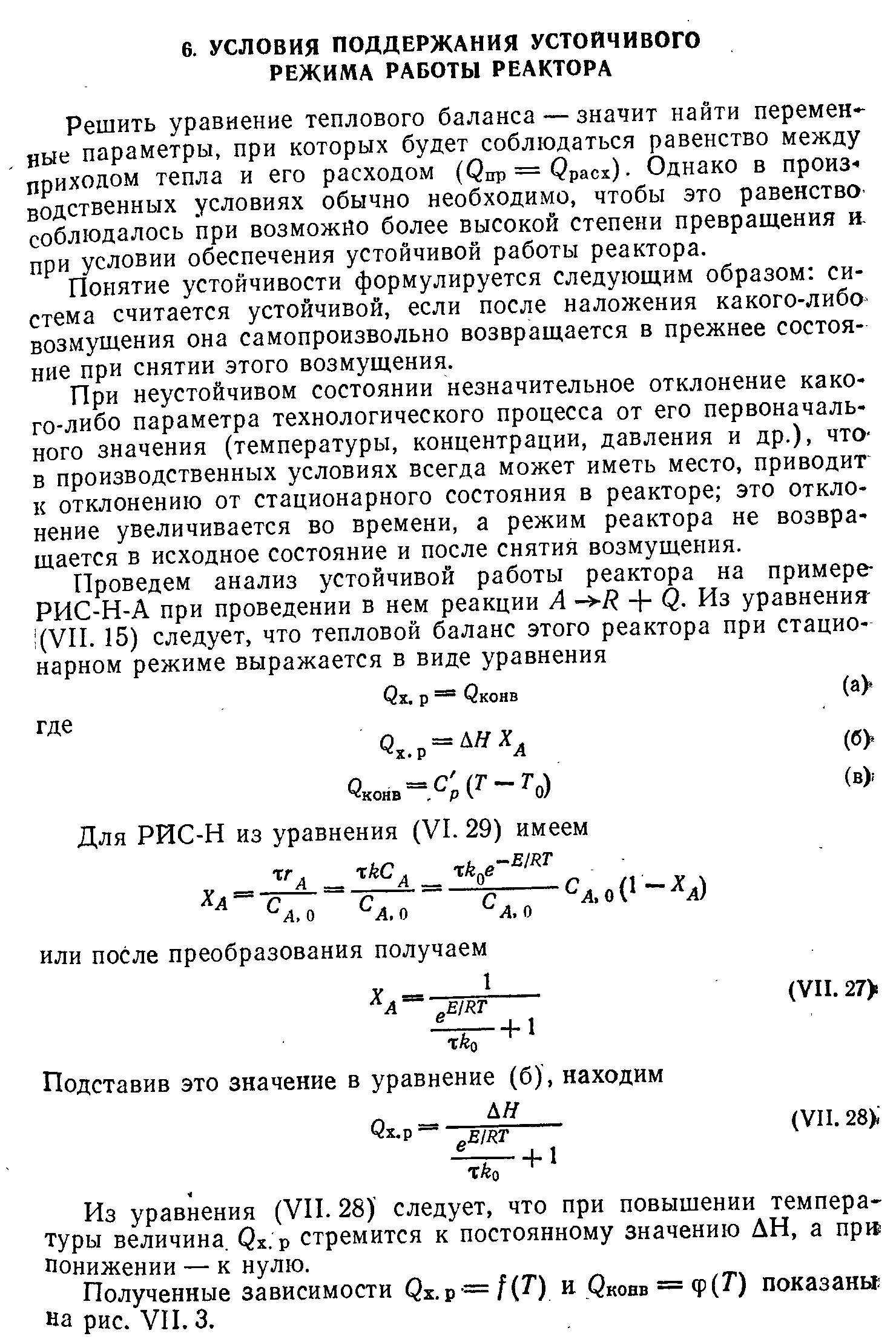       
Периодические процессы в гомогенной системе проводят в резервуарах, кубах или автоклавах, в которых реакционную смесь перемешивают каким-либо способом (рис. 4.1,в). Гораздо более разнообразны непрерывные реакторы для гомогенных систем. Это может быть и трубчатый реактор (рис. 4.1,е) и кубовый реактор с мешалкой (рис. 4.1,а), а также различные системы из этих реакторов. На рисунке 4.1 показаны основные типы реакторов для проведения гомогенных процессов.
При создании реакторов для гетерогенных процессов, необходимо принимать во внимание несколько усложняющих факторов, помимо тех, что рассматривались для гомогенных процессов. Эти факторы в значительной степени определяют конструкцию реактора. Во-первых, в гетерогенных системах компоненты находятся в различных фазах и процессы связаны с переносом вещества через поверхность соприкосновения фаз. Значительное влияние оказывают на процесс физические факторы: величина и состояние поверхности раздела фаз, диффузия вещества из одной фазы к поверхности и в объем второй фазы, а также обратная диффузия образовавшихся продуктов внутри этой фазы к ее поверхности и затем в объем первой фазы. Поэтому конструкция реакторов для гетерогенных процессов должна обеспечивать наилучшие условия для массопередачи, создавать большую поверхность соприкосновения фаз. В ряде случаев конструкция аппарата должна также создавать условия для обновления поверхности контакта фаз. При разработке гетерогенного процесса необходимо учитывать, что правильно подбирая конструкцию аппарата, можно в значительной степени интенсифицировать процесс, переводя его из одной области протекания в другую, например, снимая при интенсивном перемешивании диффузионное сопротивление, можно перевести процесс из диффузионной области в кинетическую и в дальнейшем повышать уже скорость химической реакции. Во-вторых, в гомогенных процессах мы имеем какой-либо один из известных нами режимов движения реагентов (либо смешение, либо вытеснение, либо промежуточный режим). В гетерогенных же системах каждая фаза может иметь свой режим. поэтому, возможны различны комбинации режимов контактирующих потоков. И, наконец, конструкция реактора будет зависеть от конкретного вида фаз, участвующих в реакции. Так, аппараты для осуществления реакции в системе газ–твердое (Г-Т) отличаются по конструкции от аппаратов для системы газ–жидкость (Г-Ж). Поэтому, ниже будут рассматриваться конструкции аппаратов отдельно для каждой из наиболее распространенных гетерогенных систем. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

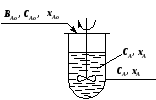
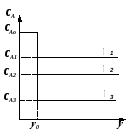
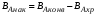
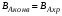
 ,
, ;
;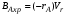 ,
,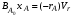 ;
;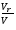 =
=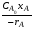
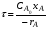
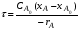
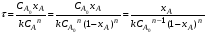
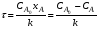
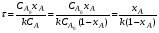
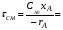
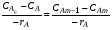
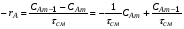
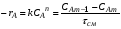
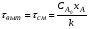 ,
,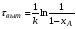 ,
,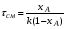 ,
,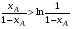
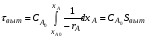 ,
,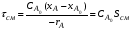 ,
,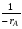 и
и 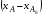 .
.
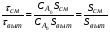
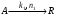 (основная реакция порядка n1),
(основная реакция порядка n1),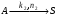 (побочная реакция порядка n2)
(побочная реакция порядка n2)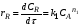 ,
,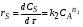 .
.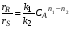
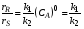
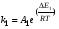 и
и 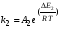
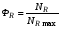 ,
,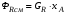
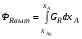
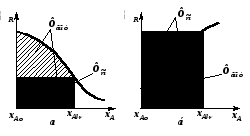
 ,
,

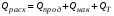 ,
,