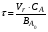ОХТ(шпоры). УКлассификация технологических процессов механические и химические технологии промышленность неорганических веществ промышадность органических веществ (включая производство и переработку пищевых продуктов)
 Скачать 3.28 Mb. Скачать 3.28 Mb.
|
Исходные положения для расчета реакторовРазработка реакторов начинается: С исследования гидродинамической модели процесса как основы его математического описания. Далее изучают кинетику химических реакций, процессы массопередачи, процессы теплопередачи. Чем глубже изучена кинетика реакций, тем надежнее предсказания результатов протекания соответствующих процессов. Кинетические уравнения, записанные в дифференциальной форме, интегрируют по объему реактора. При этом часто возникают трудности, поскольку состав и температура реакционной смеси могут различаться в разных точках реакционного пространства в зависимости от термодинамических характеристик реакций, также от скорости теплообмена с окружающей средой. Кроме того, характер движения жидкости в аппарате, определяемый реальной геометрией реактора, будет влиять на перераспределение вещества и тепла в реакторе. Поэтому для выбора конструкции и определения размеров любого реактора необходимо принимать во внимание большое число различных факторов и прежде всего располагать следующими данными:
Производительность установки (цеха), степень превращения реагентов, концентрацию реагентов и температурный режим устанавливают из ряда теоретических предпосылок. Нужно учитывать также ряд общих требований к реакторам, которые должны обеспечить:
Приведенные требования несколько противоречивы, поэтому при расчете и конструировании реакторов стремятся найти решения, обеспечивающие в конечном счете общую экономичность процесса. Одним из важнейших показателей, отражающих совершенство химического реактора, является его интенсивность, которая характеризуется количеством целевого продукта, получаемого в единицу времени при заданных условиях с единицы объема (площади) аппарата. Интенсивность аппарата тем выше, чем меньшее время затрачивают на получение заданного количества продукта. Поэтому, главной задачей при изучении процессов, протекающих в реакторах любого типа, является установление функциональной зависимости времени пребывания реагентов в реакторе от различных факторов:
Уравнение, связывающее четыре названные величины, называется характеристическим уравнением реактора. Исходным уравнением для получения характеристического уравнения реактора любого типа является материальный баланс, составленный по одному из компонентов реакционной смеси. Составим материальный баланс по исходному веществу А при проведении простой необратимой реакции:
В общем виде уравнение материального баланса записывается так:
Учитывая, что поступившее в реактор вещество А расходуется в трех направлениях, можно записать
С учетом уравнения (1.4) уравнение (1.3) записывается в виде
Разность между количеством вещества А, поступающим в единицу времени в реактор (ВАприх.) и выходящим из него (ВАст) – это количество вещества А, переносимое конвективным потоком (ВАконв):.
Принимая это во внимание, уравнение (1.5) можно записать еще в одной форме:
В каждом конкретном случае уравнение материального баланса принимает различную форму. Он может составляться для единицы объема реакционной массы либо для реактора в целом. При этом можно рассчитывать материальные потоки, проходящие через объем за единицу времени, а можно относить эти потоки к молю одного из исходных реагентов. Так, в общем случае, когда состав, температура и другие параметры непостоянны в различных точках реактора или непостоянны во времени, материальный баланс составляют в дифференциальной форме для элементарного объема реактора. В результате получают уравнение конвективного массообмена (А.Г.Касаткин. Основные процессы и аппараты химической технологии, – М: Химия, 1973.), дополненное членом rA, учитывающим протекание химической реакции. Составленное по исходному реагенту А, оно имеет вид:
Левая часть уравнения (1.8) отражает общее изменение концентрации исходного вещества во времени в элементарном объеме, для которого составляется материальный баланс. Это накопление вещества А. Левой части уравнения соответствует величина ВАнак. в уравнении баланса (1.7). Первая группа членов правой части уравнения (1.8) – произведения составляющих скорости потока вдоль осей координат на градиенты концентраций – отражает изменение концентрации А в элементарном объеме вследствие переноса его вместе с самой средой в направлении, совпадающем с направлением общего потока. Вторая группа членов правой части уравнения (1.8) – произведение Д на сумму вторых производных от концентрации по x, y, z – отражает изменение концентрации А в элементарном объеме в результате переноса его путем диффузии. Суммарному переносу вещества в движущейся среде конвективным переносом и диффузией соответствует в уравнении (1.7) величине ВАконв (суммарный перенос вещества называют конвективным массообменном или конвективной диффузией). И, наконец, член rA показывает изменение концентрации А в элементарном объеме за счет химической реакции. Ему в уравнении (1.7) соответствует величина ВАхр. В зависимости от типа реактора и режима его работы дифференциальное уравнение материального баланса (1.8) упрощается и решение его значительно облегчается. В том случае, когда параметры процесса постоянны по всему объему реактора и во времени, нет необходимости составлять баланс в дифференциальной форме. Баланс составляют в конечных величинах, беря разность значений параметров на входе в реактор и выходе из него. Все процессы, протекающие в химических реакторах, делят на:
К первым относят процессы, при которых не происходит изменения во времени параметров процесса (например, концентрации А, температуры и т.д.), поэтому в таких реакторах отсутствует накопление вещества (или тепла) и производная от параметра во времени равна нулю. Так, при стационарном режиме для компонента А:
При нестационарных режимах параметры непостоянны во времени и всегда имеется накопление вещества (тепла):
Как уже отмечалось, уравнение материального баланса является исходным при расчете реактора любого типа. Вместе с тем оно не позволяет учитывать тепловой режим в реакторе и влияние температуры на статику и кинетику процесса. Поэтому при выборе оптимального режима в реакторе, разработке методов его поддержания, расчета реакторов с теплообменной аппаратурой материальный баланс реактора должен решаться совместно с тепловым балансом. Тепловой баланс, так же как и материальный, может быть составлен в различной форме. Связующим звеном при совместном решении уравнений материального и теплового баланса служит кинетическое уравнение реакции, а также уравнение Аррениуса. Далее будут показаны методы расчета реакторов различных типов. Для этого предварительно дается классификация реакторов.
При классификации реакторов принимают во внимание следующие признаки: Характер протекающей в реакторе операции. Режим движения реакционной среды. Тепловой режим. Фазовое состояние реагентов. По первому признаку этой классификации реакторы делятся на периодические, непрерывные и полунепрерывные. Реакторы с непрерывной подачей реагентов делят, в свою очередь, по характеру движения реакционной среды (по гидродинамической обстановке в реакторе) на реакторы идеального вытеснения, реакторы идеального смешения. Классификация реакторов по тепловому режиму будет дана ниже. Обычно изучают реакторы в два этапа: вначале при работе их в изотермических условиях, когда температура реакционной смеси постоянна, а затем с учетом изменения температуры реакционной смеси. Исходным уравнением для получения характеристического уравнения реактора любого типа является материальный баланс, составленный по одному из компонентов реакционной смеси. Составим материальный баланс по исходному веществу А при проведении простой необратимой реакции:
В общем виде уравнение материального баланса записывается так:
Учитывая, что поступившее в реактор вещество А расходуется в трех направлениях, можно записать
С учетом уравнения (1.4) уравнение (1.3) записывается в виде
Разность между количеством вещества А, поступающим в единицу времени в реактор (ВАприх.) и выходящим из него (ВАст) – это количество вещества А, переносимое конвективным потоком (ВАконв):.
Принимая это во внимание, уравнение (1.5) можно записать еще в одной форме:
В каждом конкретном случае уравнение материального баланса принимает различную форму. Он может составляться для единицы объема реакционной массы либо для реактора в целом. При этом можно рассчитывать материальные потоки, проходящие через объем за единицу времени, а можно относить эти потоки к молю одного из исходных реагентов. Так, в общем случае, когда состав, температура и другие параметры непостоянны в различных точках реактора или непостоянны во времени, материальный баланс составляют в дифференциальной форме для элементарного объема реактора. В результате получают уравнение конвективного массообмена (А.Г.Касаткин. Основные процессы и аппараты химической технологии, – М: Химия, 1973.), дополненное членом rA, учитывающим протекание химической реакции. Составленное по исходному реагенту А, оно имеет вид:
Левая часть уравнения (1.8) отражает общее изменение концентрации исходного вещества во времени в элементарном объеме, для которого составляется материальный баланс. Это накопление вещества А. Левой части уравнения соответствует величина ВАнак. в уравнении баланса (1.7). Первая группа членов правой части уравнения (1.8) – произведения составляющих скорости потока вдоль осей координат на градиенты концентраций – отражает изменение концентрации А в элементарном объеме вследствие переноса его вместе с самой средой в направлении, совпадающем с направлением общего потока. Вторая группа членов правой части уравнения (1.8) – произведение Д на сумму вторых производных от концентрации по x, y, z – отражает изменение концентрации А в элементарном объеме в результате переноса его путем диффузии. Суммарному переносу вещества в движущейся среде конвективным переносом и диффузией соответствует в уравнении (1.7) величине ВАконв (суммарный перенос вещества называют конвективным массообменном или конвективной диффузией). И, наконец, член rA показывает изменение концентрации А в элементарном объеме за счет химической реакции. Ему в уравнении (1.7) соответствует величина ВАхр. В зависимости от типа реактора и режима его работы дифференциальное уравнение материального баланса (1.8) упрощается и решение его значительно облегчается. В том случае, когда параметры процесса постоянны по всему объему реактора и во времени, нет необходимости составлять баланс в дифференциальной форме. Баланс составляют в конечных величинах, беря разность значений параметров на входе в реактор и выходе из него. Все процессы, протекающие в химических реакторах, делят на:
К первым относят процессы, при которых не происходит изменения во времени параметров процесса (например, концентрации А, температуры и т.д.), поэтому в таких реакторах отсутствует накопление вещества (или тепла) и производная от параметра во времени равна нулю. Так, при стационарном режиме для компонента А:
При нестационарных режимах параметры непостоянны во времени и всегда имеется накопление вещества (тепла):
Как уже отмечалось, уравнение материального баланса является исходным при расчете реактора любого типа. Вместе с тем оно не позволяет учитывать тепловой режим в реакторе и влияние температуры на статику и кинетику процесса. Поэтому при выборе оптимального режима в реакторе, разработке методов его поддержания, расчета реакторов с теплообменной аппаратурой материальный баланс реактора должен решаться совместно с тепловым балансом. Тепловой баланс, так же как и материальный, может быть составлен в различной форме. Связующим звеном при совместном решении уравнений материального и теплового баланса служит кинетическое уравнение реакции, а также уравнение Аррениуса. Далее будут показаны методы расчета реакторов различных типов. Для этого предварительно дается классификация реакторов.
Реакторы периодические характеризуются одновременной и одноразовой загрузкой реагентов. При этом процесс складывается из трех стадий: загрузки сырья; его обработки (химического превращения); выгрузки продукта. После проведения этих операций они повторяются вновь, т.е. работа реактора осуществляется циклически.  Время одного цикла, проводимого в периодическом реакторе, определяется по уравнению Время одного цикла, проводимого в периодическом реакторе, определяется по уравнению
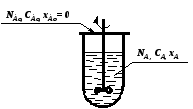
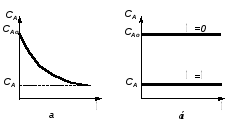
Реактор идеального смешения периодический – РИС-П – это реактор периодического действия с мешалкой (рис.2.1). Перемешивание в таком реакторе настолько интенсивное, что в каждый данный момент времени концентрация реагентов одинакова по всему объему реактора и меняется лишь во времени, по мере протекания химической реакции. Периодические процессы по своей природе всегда являются нестационарными, т.к. в них за счет химической реакции происходит изменение во времени параметров процесса, например, концентрации веществ, участвующих в реакции, т.е. имеет место накопление вещества. Для расчета периодического реактора надо знать его характеристическое уравнение, позволяющее определить рабочее время , необходимое для достижения заданной концентрации вещества CAo и известной кинетике процесса (т.е. известной зависимости скорости химической реакции – rA от концентрации реагентов и температуры).
Исходным соотношением для получения характеристического уравнения реактора, как уже говорилось, является уравнение (1.8) материального баланса в дифференциальной форме (дифференциальное уравнение конвективного массообмена). В РИС-П все параметры (в том числе и концентрация реагента А – СА) одинаковы по всему объему реактора в любой момент времени (так как реакционная смесь интенсивно перемешивается). Производная любого порядка от концентрации по x, y, z равна нулю, и поэтому можно записать:
С учетом полученных значений уравнение (1.8) упрощается и может быть записано не в частных производных, а в виде обыкновенного дифференциального уравнения:
При выражении скорости реакции по исходному веществу А: 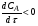 . .Поэтому, перед 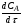 и rA ставят знак минус, чтобы скорость являлась положительной величиной. и rA ставят знак минус, чтобы скорость являлась положительной величиной.Изменение концентрации исходного вещества А во времени и по объему для реакции, протекающей в периодическом реакторе идеального смешения, показано на рисунке 2.2.
Текущую концентрацию реагента А рассчитывают по уравнению
Все реакции протекают либо без изменения, либо с изменением объема реакционной смеси. Для реакций первого типа (V=const) текущая концентрация реагента А равна
Подставив полученное значение для CA в уравнение (2.5), находим:
или
Интегрируя уравнение (2.9) в пределах изменения времени от 0 до и степени превращения от 0 до хА, получаем характеристическое уравнение РИС периодического действия для условий, когда объем реакционной смеси не изменяется в течение процесса:
Рассмотрим некоторые частные случаи этого уравнения. Для необратимой реакции n-го порядка скорость реакции выражается уравнением:
Подставив полученное значение для (-rA) в уравнение (2.10) и учитывая, что константа скорости, k, – величина постоянная в изотермических условиях, получим
Для необратимой реакции нулевого порядка
Поэтому, из уравнения (2.10) следует
Для необратимой реакции первого порядка
Поэтому подстановкой этого значения в уравнение (2.10) получаем:
или
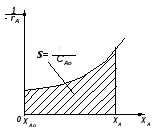
В тех случаях, когда интегрирование уравнения (2.10) связано с трудностями, определение времени производят методом графического интегрирования. Для этого строят графическую зависимость 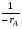 от xА и вычисляют площадь под кривой между начальным xAo и конечным xA значениями степени превращения. Для xAo=0 искомая площадь выражается уравнением (рис. 2.3): от xА и вычисляют площадь под кривой между начальным xAo и конечным xA значениями степени превращения. Для xAo=0 искомая площадь выражается уравнением (рис. 2.3):
Подставив полученное значение для S в уравнение (2.10), находим:
Приведенная на рисунке 2.1. схема РИС-П является одновременно схемой физической модели этого реактора. Если изготовить такой реактор в малом масштабе (модель промышленного реактора), а затем включить его в работу с поддержанием соответствующего технологического режима, то, исследовав такую модель, можно получить основные данные, необходимые для проектирования промышленных реакторов.
Исследование состоит в том, что опытные данные представляют в форме зависимостей безразмерных комплексов, составленных комбинацией различных физических величин и линейных размеров. Такая форма представления опытных данных позволяет распространить найденные зависимости на группу подобных между собой явлений, характеризующих постоянством определяющих безразмерных комплексов или критериев подобия (Рейнольдса, Фруда, Архимеда, Пекла, Прандтля, Куссельта и др.). Поэтому, физическое моделирование сводится к воспроизведению постоянства определяющих критериев подобия в модели и в объекте. Математической моделью РИС-П является его характеристическое уравнение (2.10). Исходя из этого уравнения, представляется возможным определить размеры реактора, а также исследовать эту модель с точки зрения определения оптимальных значений всех параметров, входящих в характеристическое уравнение. Исследование математической модели обычно проводят на электронно-вычислительной машине (ЭВМ), обладающей большими возможностями в отношении проведения вычислительных операций. Во многих случаях на основе результатов таких исследований представляется возможным вести проектирование промышленного реактора без проведения исследований на опытной установке, при условии достаточно полного изучения кинетики процесса в лабораторных условиях.
В реакторах непрерывного действия (проточные реакторы) питание их реагентами и отвод продуктов реакции осуществляется непрерывно. Если в периодическом реакторе можно непосредственно (по часам) измерять продолжительность реакции (т.к. там показатели процесса меняются во времени), то в реакторе непрерывного действия это сделать невозможно – там при установившемся режиме параметры не меняются со временем. Поэтому для непрерывных реакторов удобней пользоваться понятием условного времени пребывания реагентов в системе (времени контакта), которое определяется по уравнению:
Поскольку
выражение для τ может иметь вид:
Проточные реакторы отличаются различным характером перемещения в них вещества (гидродинамической обстановкой). По этому признаку непрерывные реакторы разделяют на реакторы идеального вытеснения и реакторы идеального смешения. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

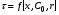 ,
,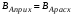 ,
,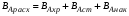 ,
,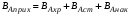
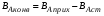
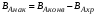
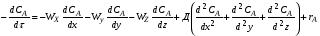 ,
,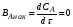
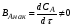
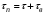 ,
,
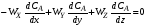 ,
,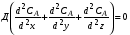
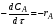
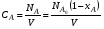
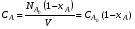
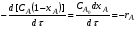
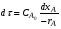
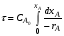
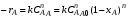
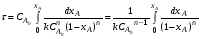
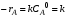
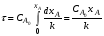
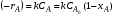
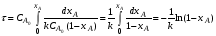
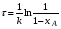
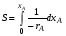
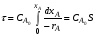
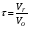 ,
,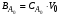 ,
,