Поурочные+планы+по+геометрии+2+часть. Урок 25 аксиома параллельных прямых цели дать представление об аксиомах геометрии ввести аксиому параллельных прямых и следствия из нее. Ход урока
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
II. Решение задач по готовым чертежам. 1. На рисунке 6 АМ = АN, 2. На рисунке 7 АD = DС, DЕ || АС, 3. На рисунке 8 ВD || АС, луч ВС – биссектриса угла АВD; = 116°. Найдите угол ВСА. 4. На рисунке 9 лучи ВО и СО – биссектрисы углов В и С треугольника АВС. На сторонах АВ и АС отмечены точки М и N так, что ВМ = МО, СN = NО. Докажите, что точки М, О и N лежат на одной прямой. 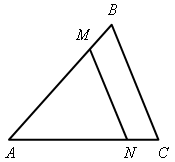 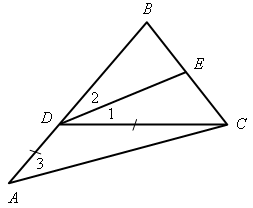 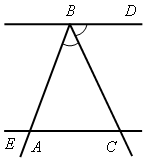 Рис. 6 Рис. 7 Рис. 8 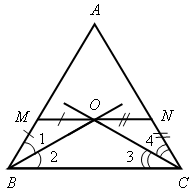 Рис. 9 IV. Итог урока. Домашнее задание: повторить материал пунктов 24–29; решить №№ 204, 207. В 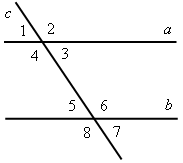 ариант I ариант I1. Сформулируйте один из признаков параллельности двух прямых. 2 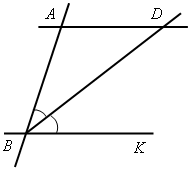 . Докажите, что прямые а и b, изображенные на рисунке 1, параллельны, если . Докажите, что прямые а и b, изображенные на рисунке 1, параллельны, если 3. На рисунке 2 прямые АD и ВK параллельны, луч ВD – биссектриса угла АВK, Вариант II 1. Сформулируйте аксиому параллельных прямых. 2 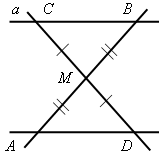 . Дан треугольник СDЕ. Сколько прямых, параллельных стороне СЕ, можно провести через вершину D? . Дан треугольник СDЕ. Сколько прямых, параллельных стороне СЕ, можно провести через вершину D?3. На рисунке 3 отрезки АВ и СD пересекаются в их общей середине М. Через точку В проведена прямая а, параллельная прямой АD. Докажите, что прямая а проходит через точку С. В  ариант I ариант I1. Сформулируйте один из признаков параллельности двух прямых. 2  . Докажите, что прямые а и b, изображенные на рисунке 1, параллельны, если . Докажите, что прямые а и b, изображенные на рисунке 1, параллельны, если 3. На рисунке 2 прямые АD и ВK параллельны, луч ВD – биссектриса угла АВK, Вариант II 1. Сформулируйте аксиому параллельных прямых. 2  . Дан треугольник СDЕ. Сколько прямых, параллельных стороне СЕ, можно провести через вершину D? . Дан треугольник СDЕ. Сколько прямых, параллельных стороне СЕ, можно провести через вершину D?3. На рисунке 3 отрезки АВ и СD пересекаются в их общей середине М. Через точку В проведена прямая а, параллельная прямой АD. Докажите, что прямая а проходит через точку С. В  ариант I ариант I1. Сформулируйте один из признаков параллельности двух прямых. 2  . Докажите, что прямые а и b, изображенные на рисунке 1, параллельны, если . Докажите, что прямые а и b, изображенные на рисунке 1, параллельны, если 3. На рисунке 2 прямые АD и ВK параллельны, луч ВD – биссектриса угла АВK, Вариант II 1. Сформулируйте аксиому параллельных прямых. 2  . Дан треугольник СDЕ. Сколько прямых, параллельных стороне СЕ, можно провести через вершину D? . Дан треугольник СDЕ. Сколько прямых, параллельных стороне СЕ, можно провести через вершину D?3. На рисунке 3 отрезки АВ и СD пересекаются в их общей середине М. Через точку В проведена прямая а, параллельная прямой АD. Докажите, что прямая а проходит через точку С. Урок 29 РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ» Цели: привести в систему знания учащихся по данной теме, подготовить учащихся к предстоящей контрольной работе. Ход урока I. II. Решение задач по готовым чертежам. 1. На рисунке 1 АЕ – биссектриса треугольника АВС, АD = DЕ, АЕ = СЕ, 2. На рисунке 2 АD – биссектриса треугольника АВС, АО = ОD, МО 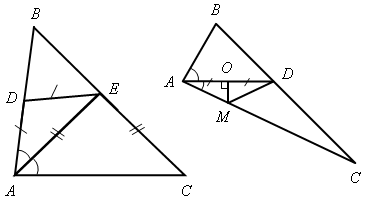 Рис. 1 Рис. 2 3. Решить задачи №№ 217, 211 (б). III. Самостоятельная работа (проверочного характера с анализом ее выполнения). Вариант I 1. На рисунке 12 прямые а и b параллельны, угол 2 на 34° больше угла 1. Найдите угол 3. 2. Через вершину прямого угла С треугольника АВС проведена прямая СD, параллельная стороне АВ. Найдите углы А и В треугольника, если Вариант II 1. На рисунке 13 прямые а и b параллельны, угол 2 в четыре раза меньше угла 1. Найдите угол 3. 2. Через вершину С треугольника СDЕ с прямым углом D проведена прямая СР, параллельная прямой DЕ. Найдите углы С и Е треугольника, если 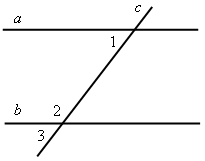 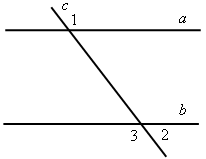 Рис. 3 Рис. 4 IV. Итог урока. Домашнее задание: подготовиться к контрольной работе, решить № 210. Урок 41 КОНТРОЛЬНАЯ РАБОТА № 3 «ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ» Цели: проверить знания, умения и навыки учащихся по теме «Параллельные прямые» и применение знаний к решению задач. Ход урока I. Организация учащихся на выполнение работы. II. Выполнение работы по вариантам. Вариант I 1. Отрезки ЕF и РD пересекаются в их середине М. Докажите, что РЕ || DF. 2. Отрезок DМ – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DМN, если Вариант II 1. Отрезки MN и EF пересекаются в их середине P. Докажите, что ЕN || MF. 2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если Вариант III (для более подготовленных учащихся) 1. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, пересекающая сторону АВ в точке Е так, что АЕ = ЕD. Найдите углы треугольника АЕD, если 2. На рисунке 14 АС || ВD, точка М – середина отрезка АВ. Докажите, что М – середина отрезка СD. Вариант IV (для более подготовленных учащихся) 1. Отрезок DM – биссектриса треугольника СDЕ. Через точку М проведена прямая, пересекающая сторону DЕ в точке N так, что DN = MN. Найдите углы треугольника DMN, если 2. На рисунке 15 АВ || DС, АВ = DС. Докажите, что точка О – середина отрезков АС и ВD. III. Итоги урока. Домашнее задание: повторить пункты 5–29. Вариант I 1. Отрезки ЕF и РD пересекаются в их середине М. Докажите, что РЕ || DF. 2. Отрезок DМ – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DМN, если Вариант II 1. Отрезки MN и EF пересекаются в их середине P. Докажите, что ЕN || MF. 2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если Вариант I 1. Отрезки ЕF и РD пересекаются в их середине М. Докажите, что РЕ || DF. 2. Отрезок DМ – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DМN, если Вариант II 1. Отрезки MN и EF пересекаются в их середине P. Докажите, что ЕN || MF. 2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если Вариант I 1. Отрезки ЕF и РD пересекаются в их середине М. Докажите, что РЕ || DF. 2. Отрезок DМ – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DМN, если Вариант II 1. Отрезки MN и EF пересекаются в их середине P. Докажите, что ЕN || MF. 2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если Вариант I 1. Отрезки ЕF и РD пересекаются в их середине М. Докажите, что РЕ || DF. 2. Отрезок DМ – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DМN, если Вариант II 1. Отрезки MN и EF пересекаются в их середине P. Докажите, что ЕN || MF. 2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если Вариант I 1. Отрезки ЕF и РD пересекаются в их середине М. Докажите, что РЕ || DF. 2. Отрезок DМ – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DМN, если Вариант II 1. Отрезки MN и EF пересекаются в их середине P. Докажите, что ЕN || MF. 2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если Вариант I 1. Отрезки ЕF и РD пересекаются в их середине М. Докажите, что РЕ || DF. 2. Отрезок DМ – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DМN, если Вариант II 1. Отрезки MN и EF пересекаются в их середине P. Докажите, что ЕN || MF. 2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если Урок 31 СУММА УГЛОВ ТРЕУГОЛЬНИКА Цели: доказать теорему о сумме углов треугольника, следствия из нее; ввести понятия остроугольного, прямоугольного и тупоугольного треугольников; рассмотреть задачи на применение доказанных утверждений. Ход урока I. Изучение нового материала. 1. Решить задачу по готовому чертежу на доске (см. рис.).
2. случайно ли сумма углов данного треугольника АВС оказалась равной 180° или этим свойством обладает любой треугольник? Поиск ответа естественно приводит к формированию теоремы о сумме углов треугольника. 3. Доказательство теоремы о сумме углов треугольника (рис. 124 учебника). 4. Устно решить задачи №№ 223 (а, б, г), 225, 226. 5. Перед введением классификации треугольников по углам (п. 31) учащимся задается вопрос: «Может ли треугольник иметь: а) два прямых угла; б) два тупых угла; в) один прямой и один тупой угол?». Ответы должны быть обоснованы с помощью теоремы о сумме углов треугольника. 6. Записать в тетрадях вывод из этих ответов (следствие из теоремы о сумме углов треугольника): в любом треугольнике либо все три угла острые, либо два угла острые, а третий – тупой или прямой. 7. Ввести понятия остроугольного, тупоугольного и прямоугольного треугольников и обратить внимание учащихся на названия сторон прямоугольника, треугольника – гипотенуза и катет (рис. 126 учебника, модели треугольников). |

