Поурочные+планы+по+геометрии+2+часть. Урок 25 аксиома параллельных прямых цели дать представление об аксиомах геометрии ввести аксиому параллельных прямых и следствия из нее. Ход урока

• Название: Урок 25 аксиома параллельных прямых цели дать представление об аксиомах геометрии ввести аксиому параллельных прямых и следствия из нее. Ход урока
• Дата: 03.11.2022
• Размер: 0.74 Mb.
• Имя файла: Поурочные+планы+по+геометрии+2+часть.doc
• Тип: Урок; #768941
• страница: 6 из 7

II. Изучение нового материала.

1. Самостоятельно (устно), используя признаки равенства треугольников, доказать признаки равенства прямоугольных треугольников по двум катетам, по катету и прилежащему острому углу, по гипотенузе и острому углу

2. Доказательство признака равенства прямоугольных треугольников по гипотенузе и острому углу (устно) по моделям равных прямоугольных треугольников.

3. Доказательство признака равенства прямоугольных треугольников по гипотенузе и катету.

III. Закрепление изученного материала.

1. Решить задачу № 261 на доске и в тетрадях.

Дано: АDС; АD = DС; АВ и СK – высоты. Доказать: АВ = СK.

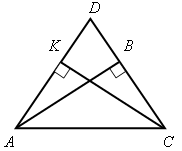
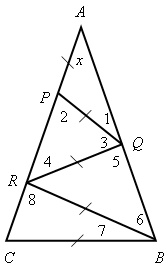
Доказательство

По условию АВ DС и СK АD, тогда АВС и АKС – прямоугольные; в них АС – общая гипотенуза и KАС = ВСА, так как по условию АDС равнобедренный.

Значит, АВС = СKА (по гипотенузе и острому углу).

Тогда АВ = СK.

3. Решить задачу № 269 на доске и в тетрадях.

Указание: при решении задачи применить вывод задачи № 268 – признак равенства прямоугольных треугольников по катету и противолежащему углу.

IV. Итоги урока.

Домашнее задание: изучить п. 35; ответить на вопросы 12–13 на с. 90; решить задачи №№ 262, 264.
Урок 40
ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ
ТРЕУГОЛЬНИКОВ

Цели: научить применять признаки равенства прямоугольных треугольников и их свойства при решении задач; вырабатывать умение решать задачи; учить логически мыслить.

Ход урока

I. Устная работа.

1. Сформулировать свойства прямоугольных треугольников.

2. Сформулировать признаки равенства прямоугольных треугольников.

3. Устно решить задачи по готовым чертежам:

1) На рисунке 1 В = С = 90°; 1 = 2. Докажите, что АВ = СD.

2) На рисунке 2 АВ = СD; ВС = АD, АFВ = СЕD = 90°. Докажите, что BF = ED; АF = EC.

3) На рисунке 3 1 = 2 = 90°, АВ = DС. Докажите, что ВС = АD.

4) На рисунке 4 АН и А₁Н₁ – высоты треугольников АВС и А₁В₁С₁; АС = А₁С₁; 1 = 2; АН = А₁Н₁.

Докажите, что 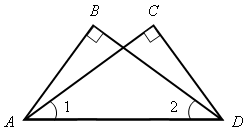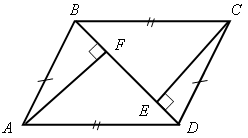АВС = А₁В₁С₁.



Рис. 1 Рис. 2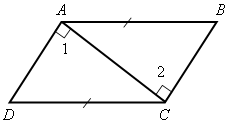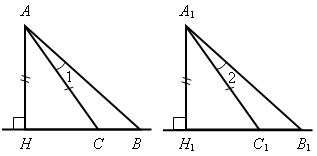



Рис. 3 Рис. 4

II. Решение задач.

1. Решить задачу № 263 на доске и в тетрадях.

2. Решить задачу № 267 на доске и в тетрадях.

Указание: при доказательстве применить признак равенства прямоугольных треугольников по гипотенузе и катету.
III. Самостоятельная работа (проверочного характера) (20 мин).

Вариант I

1. На рисунке 5 АD = DС; ЕD = DF; 1 = 2 = 90°. Докажите, что треугольник АВС равнобедренный.

2. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 18 см. Найдите гипотенузу и меньший катет.

Вариант II

1. На рисунке 6 1 = 2, 3 = 4 = 90°; ВD = DС. Докажите, что треугольник АВС равнобедренный.

2. Один из острых углов прямоугольного треугольника в два раза меньше другого, а разность гипотенузы и меньшего катета равна 15 см. Найдите гипотенузу и меньший катет.

Вариант III (для более подготовленных учащихся)

1. Через середину отрезка АВ проведена прямая а. Из точек А и В к прямой а проведены перпендикуляры АС и ВD. Докажите, что АС = ВD.

2. В прямоугольном треугольнике СDЕ с прямым углом Е проведена высота EF. Найдите CF и FD, если СD = 18 см, а DСЕ = 30°.

Вариант IV (для более подготовленных учащихся)

1. Из точки М биссектрисы неразвернутого угла О проведены перпендикуляры МА и МВ к сторонам этого угла. Докажите, что МА = МВ.

2. В прямоугольном треугольнике АВС с гипотенузой АВ и 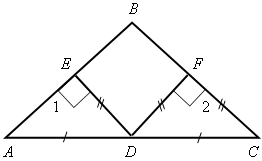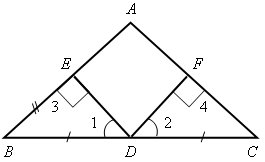А = 60° проведена высота СН. Найдите ВН, если АН = 6 см.



Рис. 5 Рис. 6

IV. Итоги урока.

Домашнее задание: повторить пункты 30–35; подготовиться к устному опросу по карточкам; прочитать п. 36; решить №№ 258, 265.
Урок 43
решение задач по теме «ПРЯМОУГОЛЬНые ТРЕУГОЛЬНИКи»

Цели: повторить и систематизировать ранее изученный материал; вырабатывать навыки в решении задач; развивать логическое мышление учащихся.

Ход урока

I. Анализ результатов самостоятельной работы.

1. Указать ошибки учащихся в решении задач.

2. Решить задачи, вызвавшие затруднения у учащихся.

II. Устный опрос учащихся по карточкам.

Вариант I

1. Сформулируйте теорему о сумме углов треугольника.

2. Один из углов при основании равнобедренного треугольника равен 65°. Найдите остальные углы треугольника.

3. В треугольнике АВС В = 110°; биссектрисы углов А и С пересекаются в точке О.

Найдите угол АОС.

Вариант II

1. Сформулируйте свойство катета прямоугольного треугольника, лежащего против угла в 30°.

2. В прямоугольном треугольнике АВС С = 90°; В = 60°, АВ =
= 15 см. Найдите ВС.

3. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 42 см. Найдите гипотенузу.

Вариант III

1. Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и катету.

2. В треугольниках АВС и А₁В₁С₁ В = В₁ = 90°; АВ = А₁В₁, АС = А₁С₁. Найдите углы А₁ и С₁ треугольника А₁В₁С₁, если А = 34°; С = 54°.

3. На сторонах угла А отмечены точки В и С так, что АВ = АС. Через точки В и С проведены прямые, перпендикулярные соответственно к сторонам АВ и АС данного угла и пересекающиеся в точке М. Докажите, что МВ = МС.

Вариант IV

1. Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и острому углу.

2. В треугольниках АВС и А₁В₁С₁углы В и В₁прямые, А = А₁, АС = А₁С₁. Найдите стороны В₁С₁ и А₁В₁ треугольника А₁В₁С₁, если ВС = 17 см, АВ = 12 см.

3. Даны два равных прямоугольных треугольника АВС и А₁В₁С₁, у которых В = В₁ = 90, А = А₁; ВН и В₁Н₁ – высоты. Докажите, что ВНС = В₁Н₁С₁.

III. Решение задач.

1. Решить задачу № 299 на доске и в тетрадях.

Решение

При решении удобно обозначить А = х и ввести обозначения цифровые для углов, как показано на рисунке. Итак, А = х, поэтому 1 = А = х, 2 = 2х (как внешний угол АРQ), 4 = = 2 = 2х; 3 = 180° – ( 2 + 4) = 180° – – 4х; 5 = 180 – ( 1 + 3) = 3х; 6 = = 5 = 3х. Далее, 7 = В – 6, но В = С = = , поэтому 7 = – 3х = = .

Так как 8 = С, то С + 8 + 7 = 2 С + 7 = 180°, или 180° – х + = 180°.

Отсюда получаем, что х = 20°. Значит, А = 20°.

Ответ: 20°.

2. Решить задачу № 311 на доске и в тетрадях.

Решение

Проведем биссектрисы углов, образованных при пересечении двух прямых, ОА и ОВ.

Возьмем произвольную точку С на одной из биссектрис и докажем, что она равноудалена от прямых ОА и ОВ, то есть докажем, что СD = СЕ. В самом деле, прямоугольные треугольники ОDС и ОЕС равны по гипотенузе (ОС – общая гипотенуза) и острому углу ( 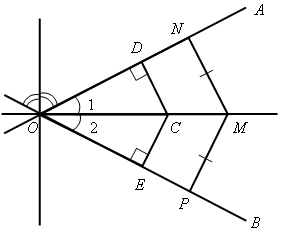1 = 2), поэтому СD = СЕ.



Докажем теперь, что любая точка М, расположенная внутри угла АОВ и равноудаленная от сторон ОА и ОВ, лежит на биссектрисе этого угла. Для этого проведем перпендикуляры MN и MP к прямым ОА и ОВ и рассмотрим прямоугольные треугольники ONM и ОРМ. Они равны по катету и гипотенузе (ОМ – общая гипотенуза, MN = MP, так как по условию точка М равноудалена от сторон ОА и ОВ), поэтому NOM = POM, то есть луч ОМ – биссектриса угла АОВ. Из доказанных утверждений следует, что искомое множество точек состоит из двух прямых, содержащих биссектрисы углов, образованных при пересечении данных прямых.