Поурочные+планы+по+геометрии+2+часть. Урок 25 аксиома параллельных прямых цели дать представление об аксиомах геометрии ввести аксиому параллельных прямых и следствия из нее. Ход урока

• Название: Урок 25 аксиома параллельных прямых цели дать представление об аксиомах геометрии ввести аксиому параллельных прямых и следствия из нее. Ход урока
• Дата: 03.11.2022
• Размер: 0.74 Mb.
• Имя файла: Поурочные+планы+по+геометрии+2+часть.doc
• Тип: Урок; #768941
• страница: 4 из 7

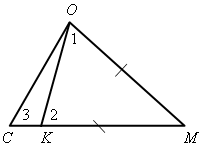
Ход урока

I. Анализ результатов самостоятельной работы.

II. Изучение нового материала.

1. Изучение нового материала необходимо начать с решения подготовительной задачи (см. рис.).

Дано: МОС; KМ = ОМ; K МС. Доказать: 1) 1 > 3; 2) МОС > 3.

Доказательство

1) Треугольник ОМK – равнобедренный с основанием ОK, поэтому 1 =  2.

Угол 2 – внешний угол треугольника ОKС, поэтому 2 >  3.

Значит, 1 = 2 и 2 > 3, следовательно, 1 > 3.

2) Так как точка K лежит на МС, то МОС > 1, а так как 1 > 3, то МОС > 3.

2. Сформулировать и доказать первое утверждение теоремы: в треугольнике против большей стороны лежит больший угол (по рис. 127 учебника).

3. Устно решить задачу № 236.

4. Перед доказательством второго утверждения теоремы (в треугольнике против большего угла лежит большая сторона) напомнить, какая теорема называется обратной данной, и предложить привести примеры обратных теорем, изученных ранее.

5. учащимся самостоятельно сформулировать утверждение, обратное первому утверждению.

На классной доске и в тетрадях учащиеся делают следующую запись:

	Теорема	Обратная теорема
Дано (условие)	АВС; АВ > АС	АВС; АСВ > АВС
Доказать (заключение)	АСВ > АВС	АВ > АС

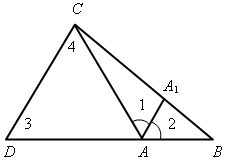
6. Доказательство обратного утверждения проводится методом от противного. В связи с этим, после того как сформулирована обратная теорема, записаны ее условие и заключение, полезно вспомнить, что при сравнении двух отрезков, например, СD и ЕF, возможен один и только один из трех случаев: СD > ЕF; СD = ЕF; СD < EF. Поэтому если мы предполагаем, что СD не больше ЕF, то возможны два случая: либо СD = ЕF, либо СD < ЕF. После этих предварительных рассуждений учащимся легче понять, почему при доказательстве теоремы, предположив, что АВ не больше АС, мы рассматриваем два возможных случая: либо АВ = АС, либо АВ < АС.

7. Устно решить задачу № 237.

8. Следствие 1 доказать

9. Следствие 2, доказать.

III. Закрепление изученного материала.

1. Решить следующие задачи (по готовым чертежам):

1) В треугольнике АВС угол С тупой, K – произвольная точка на стороне АС. Докажите, что ВK < АВ.

2) В треугольнике АВС на стороне АС отмечена точка D так, что DС = ВС. Докажите, В > А.

2. Решить задачу № 240.

IV. Итоги урока.

Домашнее задание: изучить п. 32; ответить на вопросы 6–8 на с. 89–90; решить задачи №№ 239, 241.

Урок 34
СООТНОШЕНИЯ
МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА

Цели: доказать теорему о неравенстве треугольника; учить решать задачи, используя изученные теоремы и следствия из них; развивать логическое мышление учащихся.

Ход урока

I. Организационный момент

II. Объяснение нового материала.

1. Доказательство теоремы о неравенстве треугольника.

2. Решение задачи № 251 (есть решение в учебнике на странице 75).

После этого записать в тетрадях вывод: Каждая сторона треугольника меньше суммы двух других сторон, но больше разности двух других сторон: b – с < а < b + с; а – с < b < а + с; а – b < с < а + b.

3. Устно решить задачу № 248.

III. Решение задач.

1. Решить задачу № 249.

Решение

Рассмотрим два случая:

1) стороны равнобедренного треугольника 25 см, 25 см и 10 см. По теореме о неравенстве треугольника имеем:

25 < 25 + 10 верное.

25 < 35 верное.

Значит, основание равно 10 см;

2) стороны равны 10 см, 10 см и 25 см. По теореме о неравенстве треугольника получим 25 < 10 + 10; 25 < 20 неверное.

Ответ: основание равно 10 см.

2. Самостоятельно решить задачу № 250 (а).

3. Решить задачу № 253 на доске и в тетрадях.

Решение

1) Пусть внешний угол при вершине А равнобедренного треугольника АВС острый, тогда ВАC тупой. Следовательно, ВС – основание треугольника, а потому В = С и АВ = АС.

2) ВС > АВ и ВС > АС, так как против тупого угла лежит бульшая сторона треугольника. Поэтому, учитывая условия задачи, имеем: ВС – АВ =
= 4 (см), отсюда ВС = АВ + 4.

3) АВ + АС + ВС = 25 см, или 2АВ + ВС = 25 см.

Но ВС = АВ + 4, тогда 2АВ + АВ + 4 = 25;

3АВ = 21; АВ = 7 см, ВС = 11 см, АС = 7 см.

Ответ: 7 см, 11 см, 7 см.

4. Решить задачу № 246 по рисунку 129 учебника на доске и в тетрадях.

IV. Итоги урока.

Домашнее задание: выучить материал пунктов 30–33; ответить на вопросы 1–9 на с. 89–90; решить задачи №№ 242, 250 (б, в).
Урок 35
СООТНОШЕНИЯ
МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА

Цели: повторить и обобщить изученный материал; выработать умение учащихся применять изученные теоремы при решении задач; развивать логическое мышление учащихся; подготовить учащихся к контрольной работе.

Ход урока

I. Актуализация опорных знаний учащихся.

1) ответы на вопросы 1–9 на с. 89–90;

2) устно решить задачу: существует ли треугольник со сторонами 4 м, 5 м и 8 м; со сторонами 6 см, 12 см и 3 см; со сторонами 9 дм, 9 дм и 7 дм?

II. Решение задач.

1. Решить задачу № 243 на доске и в тетрадях.

Дано: АВС; АА1 – биссектриса; СD || АА1; D АВ. Доказать: АС = АD. Доказательство Так как по условию АА1 – биссектриса треугольника АВС, то 1 = 2.

1 = 4 как накрест лежащие углы при пересечении параллельных прямых АА₁ и СD и секущей АD. Из равенств 1 = 2; 1 = 4; 2 = 3 следует, что 3 = 4, тогда по признаку равнобедренного треугольника имеем, что треугольник DАС – равнобедренный, значит, по определению АС = АD.

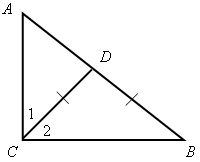
2. Решить задачу 1: в прямоугольном треугольнике АВС гипотенуза АВ = 10 см. Найдите СD, если точка D лежит на гипотенузе АВ и ВD = СD.

Дано: АВС; С = 90°; АВ = 10 см. D АВ и ВD = СD. Найти: СD. Решение 2 = В, так как по условию СD = = DВ. 1 +  2 = 90°; В + А = = 90°; но 2 = В, поэтому А =  = 1, значит, треугольник АDС – равнобедренный, тогда АD = СD.

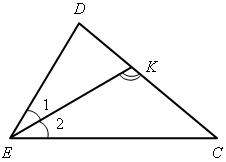
Итак, СD = ВD по условию, АD = СD по доказанному, следовательно, СD = АВ = 5 см.

Ответ: 5 см.

3. Решить задачу 2: отрезок ЕK – биссектриса треугольника DЕС.

Докажите, что KС < ЕС. Доказательство Угол ЕKС – внешний угол треугольника DKЕ,поэтому он больше угла 1 и, значит, больше угла 2, так как 1 = 2. Так как ЕKС > 2, то ЕС > KС (по теореме о соотношениях между сторонами и углами треугольника).

4. Решить задачу № 298 по рисунку 145 учебника.

III. Самостоятельная работа (15 мин).

Вариант I

В треугольнике АВС проведена биссектриса ВD, А = 75°; С = 35°.

1) Докажите, что треугольник ВDС – равнобедренный.

2) Сравните отрезки АD и DС.

Вариант II

В треугольнике СDЕ проведена биссектриса ЕF, C = 90°; D =
= 30°.

1) Докажите, что треугольник DЕF – равнобедренный.

2) Сравните отрезки CF и DF.

IV. Итоги урока.

Домашнее задание: подготовиться к контрольной работе, повторив материал пунктов 17–33; решить задачи №№ 244, 252, 297.

Вариант I

В треугольнике АВС проведена биссектриса ВD, А = 75°; С = 35°.

1) Докажите, что треугольник ВDС – равнобедренный.

2) Сравните отрезки АD и DС.

Вариант II

В треугольнике СDЕ проведена биссектриса ЕF, C = 90°; D =
= 30°.

1) Докажите, что треугольник DЕF – равнобедренный.

2) Сравните отрезки CF и DF.

Вариант I

В треугольнике АВС проведена биссектриса ВD, А = 75°; С = 35°.

1) Докажите, что треугольник ВDС – равнобедренный.

2) Сравните отрезки АD и DС.

Вариант II

В треугольнике СDЕ проведена биссектриса ЕF, C = 90°; D =
= 30°.

1) Докажите, что треугольник DЕF – равнобедренный.

2) Сравните отрезки CF и DF.

Вариант I

В треугольнике АВС проведена биссектриса ВD, А = 75°; С = 35°.

1) Докажите, что треугольник ВDС – равнобедренный.

2) Сравните отрезки АD и DС.

Вариант II

В треугольнике СDЕ проведена биссектриса ЕF, C = 90°; D =
= 30°.

1) Докажите, что треугольник DЕF – равнобедренный.

2) Сравните отрезки CF и DF.

Вариант I

В треугольнике АВС проведена биссектриса ВD, А = 75°; С = 35°.

1) Докажите, что треугольник ВDС – равнобедренный.

2) Сравните отрезки АD и DС.

Вариант II

В треугольнике СDЕ проведена биссектриса ЕF, C = 90°; D =
= 30°.

1) Докажите, что треугольник DЕF – равнобедренный.

2) Сравните отрезки CF и DF.

Вариант I

В треугольнике АВС проведена биссектриса ВD, А = 75°; С = 35°.

1) Докажите, что треугольник ВDС – равнобедренный.

2) Сравните отрезки АD и DС.

Вариант II

В треугольнике СDЕ проведена биссектриса ЕF, C = 90°; D =
= 30°.

1) Докажите, что треугольник DЕF – равнобедренный.

2) Сравните отрезки CF и DF.
Вариант I

В треугольнике АВС проведена биссектриса ВD, А = 75°; С = 35°.

1) Докажите, что треугольник ВDС – равнобедренный.

2) Сравните отрезки АD и DС.

Вариант II

В треугольнике СDЕ проведена биссектриса ЕF, C = 90°; D =
= 30°.

1) Докажите, что треугольник DЕF – равнобедренный.

2) Сравните отрезки CF и DF.

Урок 49
КОНТРОЛЬНАЯ РАБОТА № 4 «СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА»

Цели: проверить знания и умения учащихся в решении задач и применении изученного материала.