Поурочные+планы+по+геометрии+2+часть. Урок 25 аксиома параллельных прямых цели дать представление об аксиомах геометрии ввести аксиому параллельных прямых и следствия из нее. Ход урока
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
IV. Итоги урока. Домашнее задание: повторить пункты 15–33; решить задачи №№ 266, 297; принести циркули и линейки. Урок 41 РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ. РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ Цели: ввести понятия расстояния от точки до прямой и расстояния между параллельными прямыми, показать, как они применяются при решении задач. Ход урока I. Изучение нового материала. 1. Ввести понятия расстояния от точки до прямой (рис. 136): 1) понятие наклонной – отрезок АМ; 2) перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой; 3) длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой. 2. Рассмотреть рисунок 137. 3. Рассмотреть одно из важнейших свойств параллельных прямых: разобрать доказательство теоремы «все точки каждой из двух параллельных прямых равноудалены от другой прямой» по рисунку 138. 4. Ввести понятие расстояния между параллельными прямыми: расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми. 5. Справедливо утверждение, обратное доказанной теореме. Оно лежит в основе конструкции рейсмуса (рис. 139 учебника), применяемого в столярном деле для разметки прямых, параллельных краю бруска (рис. 139). II. Закрепление изученного материала. 1. Решить задачи №№ 271, 275 на доске и в тетрадях. 2. Решить задачу № 278. Указание: воспользоваться свойством катета, лежащего в прямоугольном треугольнике против угла в 30°. 3. Устно решить задачи №№ 281, 282 по готовым чертежам. III. Итоги урока. Домашнее задание: изучить п. 37; ответить на вопросы 14–18 на с. 90 учебника; решить задачи №№ 272, 277, 283; принести циркули и линейки. Урок 42 ПОСТРОЕНИЕ ТРЕУГОЛЬНИКА ПО ТРЕМ ЭЛЕМЕНТАМ Цель: рассмотреть задачи на построение треугольника по трем элементам. Ход урока I. Проверка домашнего задания. Ответить на вопросы 14–18 на с. 90. II. Объяснение нового материала. 1. Решить задачу на построение с помощью циркуля и линейки; можно рассказать о том, что обычно задачи на построение решаются по схеме, состоящей из четырех частей: 1) анализ; 2) построение; 3) доказательство; 4) исследование (описание схемы содержится в пункте «Задачи повышенной трудности к главам III и IV» на с. 92–94 учебника). Вместе с тем нужно иметь в виду, что в VII классе, как правило, следует ограничиться только выполнением и описанием построения. В отдельных случаях можно провести устно анализ и доказательство, а элементы исследования должны присутствовать лишь тогда, когда это оговорено условием задачи. 2. Рассмотреть решение задачи № 1. Построить треугольник по двум сторонам и углу между ними (рис. 140). 3. Разобрать решение задачи № 2. Построить треугольник по стороне и двум прилежащим к ней углам. 4. Решить задачу № 284 (рис. 142). (Решение приведено в учебнике на с. 87.) 5. Решить задачу № 290 (а) на доске и в тетрадях. III. Итоги урока. Домашнее задание: изучить п. 38 (1 и 2); решить задачи №№ 274, 285. Урок 43 Решение задач по теме «Прямоугольные треугольники» Цель: научить учащихся решать задачи на построение, используя циркуль и линейку. Ход урока I. Ответы на вопросы учащихся по домашнему заданию. II. Изучение нового материала. 1. Разобрать решение задачи № 3 на доске и в тетрадях. Построить треугольник по трем сторонам (рис. 141 и решение задачи на с. 85–86 учебника). Провести исследование, всегда ли задача № 3 имеет решение. 2. Решить задачи №№ 286, 289, 290 (б), 291 (в), 292, 293 на доске и в тетрадях. Решение задачи № 293 приведено в учебнике на с. 88–89. III. Самостоятельная работа (проверочного характера) (20–25 мин). Вариант I 1. Постройте прямоугольный треугольник по катету и прилежащему острому углу. 2. Даны отрезки PQ и P1Q1 и угол hk . Постройте треугольник СDЕ так, чтобы СЕ = PQ, Вариант II 1. Постройте равнобедренный треугольник по основанию и медиане, проведенной к основанию. 2. Даны отрезки PQ и P1Q1 и P2Q2. Постройте треугольник ЕKF так, чтобы ЕF = PQ, KF = P1Q1 и FD = P2Q2, где FD – высота треугольника. IV. Итоги урока. Домашнее задание: пункты 37–38; вопросы 14–20 на с. 90; решить задачи №№ 273, 287, 288, 291 (а, б, г). Урок 60 РЕШЕНИЕ ЗАДАЧ. ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ Цели: закрепить в процессе решения задач усвоение изученного материала по теме «Прямоугольные треугольники», продолжить формирование навыков в решении задач на построение. Ход урока I. Оргмомент. II. Решение задач. 1. На доске и в тетрадях решить задачи №№ 301, 302, 308, 310, 314 (б, в), 315 (а, ж, з), 318. 2. Построить прямоугольный треугольник по гипотенузе и внешнему углу при вершине острого угла. Решение Начертим данные отрезок PQ и угол hk. 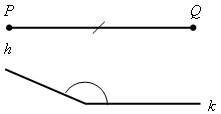 Построение 1) Проведем прямую, отметим на ней точку В и отложим отрезок ВС, равный PQ. 2) Отложим от луча ВD, являющегося продолжением луча ВС, угол DВМ, равный углу hk. 3) Построим прямую, проходящую через точку С и перпендикулярную к прямой ВМ, и обозначим буквой А точку пересечения этой прямой с лучом ВМ. Треугольник АВС искомый. Доказательство (устно) 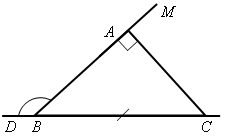 По построению треугольник АВС – прямоугольный, гипотенуза ВС равна данному отрезку РQ и внешний угол АВD треугольника равен данному углу hk. Таким образом, построенный треугольник АВС удовлетворяет всем условиям задачи. Указание: задача имеет решение только в том случае, когда данный угол hk тупой. Желательно, чтобы учащиеся сами обосновали справедливость этого утверждения. III. Итоги урока. Домашнее задание: подготовиться к контрольной работе, повторить пункты 34–38; решить задачи №№ 307, 314 (а), 315 (а). Урок 61 КОНТРОЛЬНАЯ РАБОТА № 5 «ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК» Цели: проверить знания учащихся и их умение решать задачи; выяснить пробелы в знаниях учащихся с тем, чтобы их ликвидировать на уроках повторения. Ход урока I. Организация учащихся на выполнение работы по двум вариантам. II. Выполнение учащимися работы. Вариант I 1. В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NK в точке О, причем ОK = 9 см. Найдите расстояние от точки О до прямой MN. 2. Постройте прямоугольный треугольник по гипотенузе и острому углу. Дополнительное задание. С помощью циркуля и линейки постройте угол, равный 150°. Вариант II 1. В прямоугольном треугольнике DСЕ с прямым углом С проведена биссектриса EF, причем FC = 13 см. Найдите расстояние от точки F до прямой DЕ. 2. Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу. Дополнительное задание. С помощью циркуля и линейки постройте угол, равный 105°. III. Итоги урока. Домашнее задание: повторить пункты 1–14 на с. 5–29 учебника. РЕШЕНИЕ ЗАДАЧ На четырех уроках, которые отводятся на решение задач и повторение всего учебного материала курса геометрии VII класса, полезно сконцентрировать внимание учащихся на следующих узловых вопросах курса: 1. Измерение отрезков и углов; перпендикулярные прямые (1 час). 2. Треугольники: признаки равенства треугольников; равнобедренные треугольники, сумма углов треугольника, соотношения между сторонами и углами треугольника, прямоугольные треугольники (2 часа). 3. Параллельные прямые. Решение задач (1 час). На уроках повторения следует систематизировать сведения об основных свойствах геометрических фигур, повторить доказательства отдельных наиболее важных теорем. При этом могут быть использованы заранее подготовленные карточки для устного опроса, составленные по материалу каждой главы. Целесообразно не менее половины каждого урока отводить на решение задач. Рекомендуется использовать следующие задачи учебника: 33, 36, 61, 65, 70, 82, 83, 156, 162, 170, 172, 193, 204, 208, 244, 259, 269, 286, 291, 294. Отдельным ученикам, которые проявляют особый интерес к изучению геометрии, можно предложить некоторые из задач повышенной трудности (задачи №№ 322–362). |
