Главная страница
Навигация по странице:

  • III. Итоги урока.

  • Цели

  • III. Закрепление изученного материала.

  • IV. Итоги урока. Домашнее задание

    		•

    Поурочные+планы+по+геометрии+2+часть. Урок 25 аксиома параллельных прямых цели дать представление об аксиомах геометрии ввести аксиому параллельных прямых и следствия из нее. Ход урока


    Скачать 0.74 Mb.
    НазваниеУрок 25 аксиома параллельных прямых цели дать представление об аксиомах геометрии ввести аксиому параллельных прямых и следствия из нее. Ход урока
    Дата03.11.2022
    Размер0.74 Mb.
    Формат файлаdoc
    Имя файлаПоурочные+планы+по+геометрии+2+часть.doc
    ТипУрок
    #768941
    страница5 из 7
    1   2   3   4   5   6   7

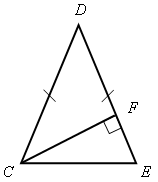
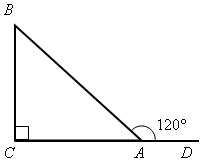
    Ход урока

    I. Организация учащихся на выполнение работы.

    II. Выполнение работы по вариантам.

    Вариант I

    1. На рисунке 1 АВЕ = 104°, DСF = 76°, АС = 12 см. Найдите сторону АВ треугольника АВС.

    2. В треугольнике СDЕ точка М лежит на стороне СЕ, причем СМD острый. Докажите, что DЕ > ДМ.

    3. Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.

    Вариант II

    1. На рисунке 2 ВАЕ = 112°, DВF = 68°, ВС = 9 см. Найдите сторону АС треугольника АВС.

    2. В треугольнике MNP точка K лежит на стороне MN, причем NKP острый. Докажите, что KР < МР.

    3. Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.

    Вариант III
    (для более подготовленных учащихся)

    1. На рисунке 1 СВМ = АСF; РАВС = 34 см, ВС = 12 см. Найдите сторону АС треугольника АВС.

    2. В треугольнике MNK K = 37°, М = 69°, NP – биссектриса треугольника. Докажите, что МР < РK.

    3. Периметр равнобедренного треугольника равен 45 см, а одна из его сторон больше другой на 12 см. Найдите стороны треугольника.

    Вариант IV
    (для более подготовленных учащихся)

    1. На рисунке 2 ЕАМ = DВF; ВС = 17 см, РАВС = 45 см. Найдите сторону АВ треугольника АВС.

    2. В треугольнике СDЕ Е = 76°, D = 66°, ЕK – биссектриса треугольника. Докажите, что KС > DK.

    3. Периметр равнобедренного треугольника равен 50 см, а одна из его сторон на 13 см меньше другой. Найдите стороны треугольника.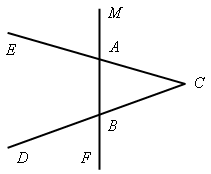



    Рис. 1 Рис. 2

    III. Итоги урока.

    В ариант I

    1. На рисунке 1 АВЕ = 104°, DСF = 76°, АС = 12 см. Найдите сторону АВ треугольника АВС.

    2. В треугольнике СDЕ точка М лежит на стороне СЕ, причем СМD острый. Докажите, что DЕ > ДМ.

    3. Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.



    Вариант II

    1. На рисунке 2 ВАЕ = 112°, DВF = 68°, ВС = 9 см. Найдите сторону АС треугольника АВС.

    2. В треугольнике MNP точка K лежит на стороне MN, причем NKP острый. Докажите, что

    KР < МР.

    3. Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.

    В ариант I

    1. На рисунке 1 АВЕ = 104°, DСF = 76°, АС = 12 см. Найдите сторону АВ треугольника АВС.

    2. В треугольнике СDЕ точка М лежит на стороне СЕ, причем СМD острый. Докажите, что DЕ > ДМ.

    3. Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.



    Вариант II

    1. На рисунке 2 ВАЕ = 112°, DВF = 68°, ВС = 9 см. Найдите сторону АС треугольника АВС.

    2. В треугольнике MNP точка K лежит на стороне MN, причем NKP острый. Докажите, что

    KР < МР.

    3. Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.

    В ариант I

    1. На рисунке 1 АВЕ = 104°, DСF = 76°, АС = 12 см. Найдите сторону АВ треугольника АВС.

    2. В треугольнике СDЕ точка М лежит на стороне СЕ, причем СМD острый. Докажите, что DЕ > ДМ.

    3 . Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.

    Вариант II

    1. На рисунке 2 ВАЕ = 112°, DВF = 68°, ВС = 9 см. Найдите сторону АС треугольника АВС.

    2. В треугольнике MNP точка K лежит на стороне MN, причем NKP острый. Докажите, что

    KР < МР.

    3. Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.

    Урок 37
    ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ И ИХ НЕКОТОРЫЕ СВОЙСТВА

    Цели: рассмотреть некоторые свойства прямоугольных треугольников и показать, как они применяются при решении задач.

    Ход урока

    I. Анализ результатов контрольной работы.

    II. Изучение нового материала.

    1. Устно решить задачу № 254

    2. Решить задачу № 255 на доске и в тетрадях.
    Дано: СDЕ; СD = DЕ; СF DЕ;

    D = 54°.

    Найти: ЕСF.

    Решение

    По условию треугольник СDЕ – равнобедренный, тогда Е = DСЕ = (180° – 54°) :
    : 2 = 63° (углы при основании равнобедренного треугольника равны).

    Так как СF DЕ по условию, то треугольник СFЕ – прямоугольный, в нем CFЕ = 90°, Е = 63°; тогда ЕСF = 180° – (90° + 63°) = 27°.

    Ответ: 27°.

    3. Рассмотреть свойство 1°

    4. Доказательство свойств 2° и 3°




    Теорема
    Обратная теорема

    Дано

    АВС; А = 90°

    В = 30°
    АВС; А = 90°,

    АС = ВС

    Доказать

    АС = ВС
    В = 30°

    III. Закрепление изученного материала.

    1. Устно решить задачи по готовым чертежам на доске: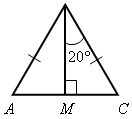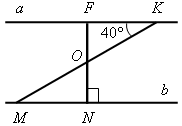



    Рис. 1 Рис. 2

    1) Дано: АВС (рис. 1).

    Найти: углы АВС.

    2) Дано: а || b (рис. 2).

    Найти: углы треугольника MON.

    2. Решить задачу № 257 на доске и в тетрадях.



    Рис. 3
    Дано: АВС (рис. 3); C = 90°,

    ВАD = 120° внешний угол;

    АС + АВ = 18 см.

    Найти: АС и АВ.

    Решение

    CАВ = 180° – 120° = 60° (смежные углы), тогда В = 90° – 60° =
    = 30° (по свойству 1°); АС = АВ (свойство 2°; катет, лежащий против угла в 30°).

    По условию АС + АВ = 18 см; АВ + АВ = 18 см; 1 АВ = 18 см, АВ = 12 см; значит, АС = 18 – 12 = 6 (см).

    Ответ: АВ = 12 см; АС = 6 см.

    3. Решить задачу № 260.



    Рис. 4
    Дано: DМС (рис. 4); DМ = МС; МО DС; DМ = 15,2 см; МО = 7,6 см.

    Найти: углы DМС.

    Решение

    Так как МО = DМ, то по свойству 3° D = 30°, тогда С = 30°, М =
    = 180° – (30° + 30°) = 180° – 60° = 120°.

    Ответ: D = С = 30°; М = 120°.

    IV. Итоги урока.

    Домашнее задание: изучить п. 34; повторить пункты 15–33; ответить на вопросы 10 и 11 на с. 90; решить №№ 256, 259.

    Урок 39
    ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ
    ТРЕУГОЛЬНИКОВ

    Цели: доказать признаки равенства прямоугольных треугольников и показать, как они применяются при решении задач.

    Ход урока

    I. Повторение изученного материала.

    1. Сформулировать свойства прямоугольных треугольников.

    2. Вспомнить признаки равенства треугольников.

    3. Решить задачу: гипотенузы ВD и АС прямоугольных треугольников АВD и АВС с общим катетом АВ и с равными катетами АD и ВС пересекаются в точке О (см. рис.). Докажите, что треугольник АОВ равнобедренный.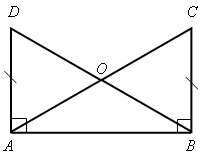


    1   2   3   4   5   6   7

    написать администратору сайта