конспект шахматы. КОНСПЕКТ ШАХМАТЫ. Урок первый. Знакомство с шахматами
 Скачать 6.14 Mb. Скачать 6.14 Mb.
|
Урок двадцать третий. Правило квадрата шахматной пешки.Пройдет ли шахматная пешка в ферзи? Сегодня король находится достаточно далеко от своей пешки и не успевает ей помочь. Теперь всё зависит от того, где расположен король противника, и далеко ли от поля превращения находится пешка. Большое значение имеет и очередь хода. Пешка бежит в ферзи, а король чёрных стремится задержать её. Начинающий тыкает пальцами во все клетки: «Я сюда, он туда, я сюды, он туды!» При таком подсчёте случаются ошибки. Выучи правило, которое поможет тебе сразу определить, как закончится борьба в этом окончании. Называется оно правило квадрата пешки. Сначала построим квадрат, сторона которого будет равна количеству клеток от пешки до поля превращения, включая и то поле, на котором находится пешка. Для белой пешки h4 квадратом станет h4 – h8 – d8 – d4. Если король слабейшей стороны находится в квадрате пешки или при своём ходе попадает в него, то он задерживает пешку. Получается, что при своём ходе король попадает в квадрат, успеет задержать пешку и уничтожить её. При ходе белых – пешка успеет стать ферзём. Проверим, так ли это на самом деле. Но надо учитывать, что квадрат уменьшается по мере продвижения пешки. Итак, при ходе 1. h4–h5 Kpc4–d5 2. h5–h6 Kpd5–e6 3. h6–h7 Kpe6–f7 4. h7–h8Ф. Чёрный король со всех ног бежал, но так и не успел догнать пешку. Она проскакивает в ферзи.  Гораздо труднее придётся белым, если не они ходят первыми. В этом окончании надо сразу обратить внимание на то, как при движение пешки меняется (уменьшается) КВАДРАТ. 1. . . . Kpc4 – d4! Король сразу попадает в квадрат пешки. Квадрат пока большой 5 на 5. 2. h4 – h5 Kpd4 – e5 Теперь король по диагонали после каждого хода впрыгивает в квадрат ускользающей пешки. 3. h5 – h6 Kpe5 – f6 После последнего хода квадрат уже стал 3 на 3. Король в квадрате, и он успевает догнать пешку.  4. h6 – h7 Kpf6 – g7 5. h7 – h8Ф+ Kpg7 : h8 Королевская погоня закончилась в квадрате 1 на 1. Пешка уничтожена. Строя квадрат, учитывай, где находится пешка. Легко ошибиться, определяя границы пешки как g2–g8. Если пешка стоит на 2-й горизонтали, считай что она уже на 3-й линии. Первый ход пешка может сделать на две клетки! Для пешки, стоящей на а2, квадрат (a3 – a8 – f3 – f8). Понятно, что король, даже при своём ходе, не попадает в квадрат белой пешки. 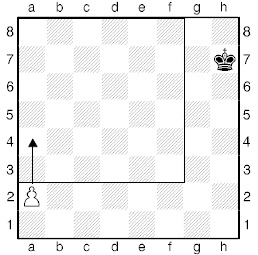 Внимательно посмотри, встретится ли на пути короля, который стремится в квадрат пешки, какое-либо препятствие? Тогда его придётся обходить, и можно не успеть оказаться у цели. Кажется, что наш король первым ходом попадает в квадрат пешки d4 (d4 – d1 – g4 – g1).  Но неожиданно король встречает препятствие в виде своей же пешки f3, которую приходится обходить, теряя темпы. Как хотелось бы пешку съесть! 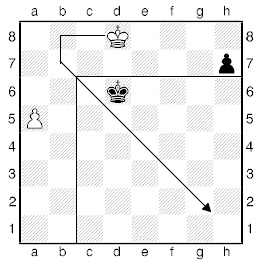 На тему «квадрата» посмотри позицию этюдиста Л. Прокеша. 1. Kpd8 – c8! Kpd6 – c6 Куда идёт король? Почему он удаляется от опасной проходной пешки? Хочется, но нельзя королю в другую сторону 1. Kpd8–e8? h7–h5 2. Kpe8–f7 h5–h4 3. a5–a6 Kpd6–c6 4. a6–a7 Kpc6–b7. Оказывается, король помог своей пешке. 2. Kpc8 – b8! Kpc6 – b5 Вновь король удаляется от опасной проходной. Чёрный король вынужден подняться вверх, уступая горизонталь – поле b6 под контролем пешки. 3. Kpb8 – b7 Kpb5 : a5 А бить пешку чёрный король был вынужден. Белый король поднимается на освободившуюся линию. А чёрный король уступил ему дорогу. 4. Kpb7 – c6 h7 – h5 Теперь белый король в «квадрате пешки» h7, несмотря на её длинный прыжок. 5. Kpc6 – d5 h5 – h4 6. Kpd5 – e4 h4 – h3 7. Kpe4 – f3 h3 – h2 8. Kpf3 – g2. Вот таким обманным движением белый король и решил свою задачу. Обрати внимание, что горизонтали белый король не проигрывал. |
