математиака. Урок предмет математика
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
IV. Знакомство с определением времени по часам. Учитель просит учащихся рассмотреть рисунок учебника (с. 49, часть 1). – Что на нём изображено? (Часы.) – Для чего нужны часы? (Определять время.) – Умеете ли вы определять время по часам? – Вы, конечно, знаете, что время показывают удивительные стрелочки, которые движутся по циферблату. Обычно у часов 2 стрелки. Одна двигается медленно-медленно, еле-еле. Посмотрите, какая она толстая и короткая. (Учитель показывает часовую стрелку на модели часов.) Другая стрелка двигается по кругу побыстрее. Вон она какая длинная и тонкая. (Показ минутной стрелки на модели часов.) У каждой из них своя работа и своё имя. Короткая и толстая стрелка – часовая. – Как вы думаете, почему её так назвали? – Тонкая и длинная стрелка – минутная. – Она показывает… (минуты). – Но довольно часто можно встретить часы, у которых не две, а три стрелки. Третья стрелка – самая маленькая и самая «шустрая», она отсчитывает секунды. Далее учитель просит учеников внимательнее рассмотреть часы на рисунке в учебнике. – Что в них общего? (У всех минутная стрелка стоит на 12.) Учитель сообщает детям о том, что если минутная стрелка стоит на 12, то часы показывают только число часов, без минут. Далее учитель просит детей расположить часы по порядку возрастания времени, которое они показывают. Р а б о т а в т е т р а д и. Учитель просит учеников рассмотреть часы в задании 4 (с. 11 в тетради № 1). – Что заметили? (У этих часов пропущены некоторые цифры.) – Впишите недостающие цифры и определите время, которое показывают часы. В з а и м о п р о в е р к а. V. Работа над развитием внимания, наблюдательности учащихся. В заключение урока ученики выполняют задание, способствующее развитию наблюдательности и внимания: сравнивают рисунки на полях учебника (с. 48, часть 1). VI. Итог урока. – Что хотите сказать? – Что особенно запомнилось? У р о к 30. ЧИСЛА 1, 2, 3, 4, 5, 6, 7. ЦИФРА 7 Цели урока: закреплять у учащихся знание состава чисел 2–7; упражнять детей в записи и чтении равенств; продолжать формировать умение детей составлять и читать неравенства, соотносить число с цифрой; учить писать цифру 7. Ход урока I. Организационный момент. II. Упражнение в умении логически мыслить. Учителю можно начать урок с задания на смекалку. С этой целью может быть использовано задание 2 (с. 49 учебника, часть 1). – Какую фигуру чертит заяц? (Круг или шестиугольник.) – Объясните, как рассуждали. – Какую фигуру начертила белочка? (Шестиугольник.) – Почему так решили? III. Упражнение в счёте предметов и соотнесении числа с цифрой. Учитель выставляет на наборное полотно разноцветные квадраты и круги. (Может быть использовано задание 2 учебника, с. 49, часть 1.) – Каким по счёту будет красный квадрат, если считать справа налево? – Каким по счёту будет зелёный квадрат? – Сколько всего квадратов? – Каким по счёту будет жёлтый кружок, если считать слева направо? – Каким будет розовый кружок? – Сколько кружков всего? Р а б о т а в т е т р а д и. Учащиеся выполняют с а м о с т о я т е л ь н о задание 1 (с. 13 в тетради № 1): соотносят количество предметов с цифрой, записанной ниже. В з а и м о п р о в е р к а. Учитель выставляет на наборное полотно различные предметы и просит детей цифрой записать их количество. Например,5 тигрят, 3 котёнка, 1 голубь, 6 грибов, 7 шариков. (Учащиеся не смогут записать количество шариков, так как не учили написание цифры 7.) – Почему вы не смогли записать число шариков? Чему мы должны научиться, чтобы выполнить задание? (Научиться писать цифру 7.) Учитель вывешивает на доску увеличенный образец цифры 7. IV. Знакомство с цифрой 7. 1. Подготовка учащихся к восприятию цифры 7. Анализ образца. Вот семёрка – кочерга. У неё одна нога. С. Маршак – А что вам напоминает цифра 7? 2. Письмо цифры по э т а п а м: в воздухе; по точкам; самостоятельно (с. 13 в тетради № 1, задание 6).  3. Упражнение в умении определять состав числа. Р а б о т а в т е т р а д и. На доске записаны числа из задания 6 (ч. 2, с. 13 в тетради № 1): 1, 2, 4, 5, 6, 7. 7, 6, 5, 3, 2, . – Что хотите сказать? – Какие числа пропущены? – Запишите пропущенные числа соответствующей цифрой в ваших тетрадях. – В каком порядке записаны числа верхней строки? – В каком порядке записаны числа нижней строки? – А как они расположены на числовой прямой? V. Чтение и составление равенств. Игра «Назови соседа»: 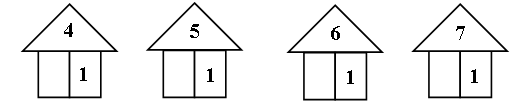 (При выполнении этого задания ученики могут воспользоваться числовой прямой: – Сколько «шагов» нужно сделать от 1 до 4? (Три. Значит, пропущено число 3.) После того как назван каждый «сосед», учащиеся составляют равенства и записывают их на доске и в тетрадях. 4 = 3 + 1 6 = 5 + 1 5 = 4 + 1 7 = 6 + 1  VI. Формирование умения читать и составлять неравенства. На магнитной д о с к е учитель магнитными цифрами записывает следующее: 4 5 6 3 7 1 2 3 – Что хотите сказать? – Поставьте нужные знаки. – Как называются полученные записи? (Неравенства.) – Прочитаем их хором. Р а б о т а в т е т р а д и. Далее учитель просит детей прочитать неравенства в задании 4 (с. 13 в тетради № 1) и раскрасить рисунки в соответствии с записью. – Какая запись «лишняя»? (4 = 4.) – Почему? (Это равенство.) VII. Работа с геометрическим материалом. Р а б о т а с у ч е б н и к о м. Учитель предлагает детям рассмотреть задание 2 (с. 51, часть 1). – Как называются изображённые линии? (Отрезки.) – Как вы узнали, что это – отрезки? – Как вы думаете, есть ли среди отрезков, изображённых на рисунке, отрезки, имеющие одинаковую длину? – Как это проверить? (Учащиеся измеряют длины отрезков при помощи мерки.) VIII. Итог урока. – Чему учились на уроке? – Какие открытия сделали? – Какую бы работу вам хотелось выполнить ещё? У р о к 31. ЧИСЛА 1, 2, 3, 4, 5, 6, 7 Цели урока: показать учащимся, что при прибавлении к числу единицы получается следующее за ним число, а при вычитании из числа единицы получается предыдущее число; познакомить учеников с терминами «последующее число», «предыдущее число»; продолжать пропедевтику темы «Задача»; закреплять знания учащихся о числах 1–7. Ход урока I. Организационный момент. II. Закрепление знаний учащихся о числах 1–7. Повторение состава изученных чисел. Н а д о с к е з а п и с ь: 1 3 5 7 – Что заметили? (Пропущены числа.) – Вставьте пропущенные числа. – Как называется полученная запись? (Отрезок числового ряда; отрезок числовой прямой.) – Как в числовом ряду должны быть расположены числа? (В порядке увеличения; в порядке возрастания.) Далее учитель предлагает рассмотреть учащимся задание на доске и сказать, какие ошибки в нём допущены. 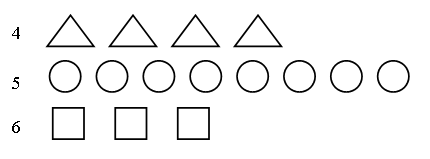 – Какие ошибки допущены? (Около цифры 5 число кружков больше пяти; около цифры 6 число квадратиков меньше.) – Исправьте ошибки. (Учащиеся зачёркивают «лишние» кружки, дорисовывают недостающие квадраты.) Затем учитель предлагает ученикам рассмотреть следующую запись на д о с к е: 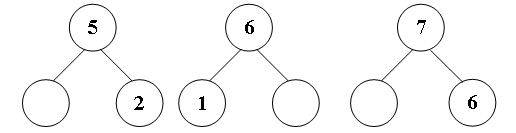 Для выполнения этого задания можно использовать числовую прямую. Состав чисел дети проговаривают хором: Пять – это три и два. Шесть – это один и пять. Семь – это шесть и один.  III. Изучение нового материала. 1. Знакомство с новыми понятиями. Учитель может использовать задание 1 (с. 50 учебника, часть 1) и числовую прямую, на которой записаны уже выученные детьми числа: 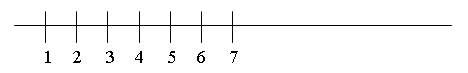 – Какое число получится, если к 1 прибавить 1? (Два.) – Где на числовой прямой расположено число 2 по отношению к числу 1? (Оно следует за ним.) – Какое число получится, если к 2 прибавить 1? (Три.) – Как расположено на числовой прямой число 3 по отношению к числу 2? (Следует за ним.) – Что можно сказать о числах 3 и 4? (Число 4 следует за числом 3.) – Какое число надо прибавить к числу 3, чтобы получить число 4? (Один.) И т. д. В процессе работы на доске появляется з а п и с ь: 1 + 1 = 2 2 + 1 = 3 3 + 1 = 4 4 + 1 = 5 5 + 1 = 6 6 + 1 = 7 – Посмотрите внимательно на составленные вами равенства. – Какой в ы в о д можно сделать? (Если к числу прибавить 1, то получится следующее за ним число.) Учитель сообщает учащимся о том, что в математике число, которое следует за другим, называют последующим. Далее учитель спрашивает учеников о том, какое число получится, если из 7 вычесть 1? (Шесть.) – Как расположено на числовой прямой число 6 по отношению к числу 7? (Стоит перед ним.) – Какое число получится, если из 6 вычесть 1? (Пять.) – Как число 5 на числовой прямой расположено по отношению к числу 6? (Стоит перед ним.) – Как по отношению друг к другу расположены числа 4 и 5? (Число 4 стоит перед числом 5.) – Какое число нужно вычесть из числа 5, чтобы получить число 4? (Один.) И т. д. В процессе работы на д о с к е появляется следующая з а п и с ь: 7 – 1 = 6 6 – 1 = 5 5 – 1 = 4 4 – 1 = 3 3 – 1 = 2 2 – 1 = 1 – Сравните полученные равенства. – Что заметили? – В математике число, которое при счёте (и на числовой прямой) расположено перед другим числом, называется предыдущим.  2. Формирование умения определять, какое число пропущено. Учащиеся под руководством учителя выполняют задание 3 (с. 50 учебника, часть 1). Данное задание выполняется устно; ученики, рассуждая, приходят к в ы в о д у о том, какое число пропущено. Правильность выполнения задания проверяется по числовой прямой. Затем с комментированием выполняется задание 5 (с. 13 в тетради № 1). IV. Пропедевтика темы «Задача». Учителем может быть использовано задание 1 (с. 51 учебника, часть 1). Учащиеся, выполняя задание, по рисункам составляют краткие рассказы, содержащие вопрос, и соотносят числовые выражения с рисунками и составленными рассказами. V. Итог урока. – Что нового узнали на уроке? – Оцените свою работу на уроке. |
