Курсовая работа. Готовая курсовая работа. Установление закона распределения времени безотказной работы системы по известным законам распределения элементов
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
Законы распределенияДля анализа надёжности систем методом статистического моделирования мы рассмотрим следующие 4 распределения: Распределение Вейбулла  Это довольно универсальное распределение, охватывающее путем варьирования параметров широкий диапазон случаев изменения вероятностей. Наряду с логарифмически нормальным распределением оно удовлетворительно описывает наработку деталей и узлов технологического оборудования по усталостным разрушениям, наработку до отказа подшипников, электроламп и т.п. Оно применяется также для оценки надежности по приработочным отказам. Распределение Вейбулла описывается функцией плотности вероятности следующего вида Это довольно универсальное распределение, охватывающее путем варьирования параметров широкий диапазон случаев изменения вероятностей. Наряду с логарифмически нормальным распределением оно удовлетворительно описывает наработку деталей и узлов технологического оборудования по усталостным разрушениям, наработку до отказа подшипников, электроламп и т.п. Оно применяется также для оценки надежности по приработочным отказам. Распределение Вейбулла описывается функцией плотности вероятности следующего вида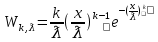 (6) (6)где 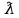 ( (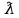 > 0) - интенсивность событий (аналогично параметру экспоненциального распределения), а k - показатель нестационарности (k > 0). При k = 1, распределение Вейбулла вырождается в экспоненциальное распределение, а в остальных случаях описывает поток независимых событий с нестационарной интенсивностью. При k > 1 моделируется поток событий с растущей со временем интенсивностью, а при k < 1 - со снижающейся. Область определения функции распределения плотности вероятностей: неотрицательные действительные числа. > 0) - интенсивность событий (аналогично параметру экспоненциального распределения), а k - показатель нестационарности (k > 0). При k = 1, распределение Вейбулла вырождается в экспоненциальное распределение, а в остальных случаях описывает поток независимых событий с нестационарной интенсивностью. При k > 1 моделируется поток событий с растущей со временем интенсивностью, а при k < 1 - со снижающейся. Область определения функции распределения плотности вероятностей: неотрицательные действительные числа. Гамма распределениеГамма - распределение в теории вероятностей - это двухпараметрическое семейство абсолютно непрерывных распределений. Если параметр k принимает целое значение, то такое гамма-распределение также называется распределением Эрланга. Пусть распределение случайной величины X задаётся плотностью вероятности, имеющей вид 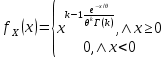 (7) (7)где функция Г(k) имеет вид Г(k) = 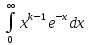 (8) (8)и обладает следующими свойствами: 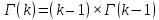 ; ; 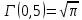 ; константы k, θ > 0. ; константы k, θ > 0.Тогда говорят, что случайная величина X имеет гамма-распределение с положительными параметрами θ и k. Пишут 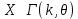 . . Экспоненциальное распределение Экспоненциальное распределение описывает интервалы времени между независимыми событиями, происходящими со средней интенсивностью Экспоненциальное распределение описывает интервалы времени между независимыми событиями, происходящими со средней интенсивностью 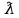 . Количество наступлений такого события за некоторый отрезок времени описывается дискретным распределением Пуассона. Экспоненциальное распределение вместе с распределением Пуассона составляют математическую основу теории надёжности. . Количество наступлений такого события за некоторый отрезок времени описывается дискретным распределением Пуассона. Экспоненциальное распределение вместе с распределением Пуассона составляют математическую основу теории надёжности.Кроме теории надёжности, экспоненциальное распределение применяется в описании социальных явлений, в экономике, в теории массового обслуживания, в транспортной логистике - везде, где необходимо моделировать поток событий. Экспоненциальное распределение является частным случаем распределения хи-квадрат (для n=2), а следовательно, и гамма-распределения. Так-как экспоненциально распределённая величина является величиной хи-квадрат с 2-мя степенями свободы, то она может быть интерпретирована как сумма квадратов двух независимых нормально распределенных величин. Кроме того, экспоненциальное распределение является честным случаем распределения Вейбулла. Дискретный вариант экспоненциального распределения - это геометрическое распределение. Плотность вероятности экспоненциально распределения: 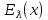 = =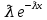 (9) (9)определена для неотрицательных действительных значений 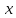 . .Если функцию плотности вероятностей экспоненциального распределения отразить зеркально в область отрицательных значений, то есть, заменить 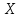 на на 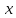 , то получится распределение Лапласа, также называемое двойным экспоненциальным или двойным показательным. , то получится распределение Лапласа, также называемое двойным экспоненциальным или двойным показательным.Нормальное распределение Нормальное распределение, также называемое распределением Гаусса или Гаусса - Лапласа — распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса: Нормальное распределение, также называемое распределением Гаусса или Гаусса - Лапласа — распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса: 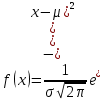 (10) (10)где параметр 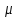 - математическое ожидание (среднее значение), медиана и мода распределения, а параметр - математическое ожидание (среднее значение), медиана и мода распределения, а параметр 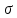 - среднеквадратическое отклонение - (σ2 - дисперсия) распределения. - среднеквадратическое отклонение - (σ2 - дисперсия) распределения.Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений, которое принадлежит экспоненциальному классу распределений. Многомерный случай описан в статье «Многомерное нормальное распределение». Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 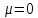 и стандартным отклонением и стандартным отклонением 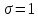 . . |
