Курсовая работа. Готовая курсовая работа. Установление закона распределения времени безотказной работы системы по известным законам распределения элементов
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
Числовые характеристики выборкиЧисловые характеристики выборки - это параметры выборки, выражающие наиболее существенные особенности статистического распределения выборки. Выборочное среднееВыборочное среднее - это приближение теоретического среднего распределения, основанное на выборке из него. Пусть X1, …, Xn, …- выборка из распределения вероятности, определённая на некотором вероятностном пространстве. Тогда её выборочным средним называется случайная величина 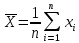 (11) (11)Выборочная дисперсия Выборочная дисперсия в математической статистике - это оценка теоретической дисперсии распределения, рассчитанная на основе данных выборки. Виды выборочных дисперсий: Выборочная дисперсия в математической статистике - это оценка теоретической дисперсии распределения, рассчитанная на основе данных выборки. Виды выборочных дисперсий:1) смещённая 2) несмещённая или исправленная Пусть X1, …, Xn {\displaystyle X_{1},\ldots ,X_{n},\ldots } — выборка из распределения вероятности. Тогда выборочная дисперсия — это случайная величина
|
| X1 | X2 | X3 | V |
| U(18;30) | U(18;30) | N(30; 5) | G(0,6) |
В таблице 1 приняты следующие обозначения законов распределения:
N - нормальное распределение;
U - равномерное распределение;
G - геометрическое распределение;
В скобках указаны параметры распределений.
На листе Excel (таблица 2) предусмотрим место для значений случайных величин. Колонки А и В - вспомогательные, в них заносятся равномерно распределенные случайные числа (РРСЧ) из промежутка [0; 1]. В колонки С, D, Е и F заносятся значения заданных случайных величин Х1, Х2, Х3 и V соответственно, полученные путем преобразования РРСЧ. Колонка G служит для значений случайной величины Y, а колонка Н- для значений случайной величины Z.
Таблица 2 - Получение случайных чисел
| РРСЧ | РРСЧ | X1 | X2 | X3 | V | Y | Z |
 0,243965 0,243965 | 0,051945 | 18,80972 | 39,43417 | 12,43965382 | 2 | 31,24937 | 31,44937 |
| 0,864273 | 0,052534 | 1,944885 | 39,28404 | 18,64273198 | 1 | 20,58762 | 20,68762 |
| 0,846289 | 0,350276 | 2,225254 | 13,98711 | 18,4628928 | 1 | 13,98711 | 14,08711 |
| 0,319926 | 0,77022 | 15,19553 | 3,481051 | 13,19926194 | 1 | 3,481051 | 3,581051 |
| 0,760764 | 0,900252 | 3,645764 | 1,40108 | 17,60763859 | 1 | 1,40108 | 1,50108 |
| 0,476378 | 0,984108 | 9,887257 | 0,213589 | 14,76377692 | 1 | 0,213589 | 0,313589 |
| 0,11437 | 0,99738 | 28,91089 | 0,034978 | 11,14369936 | 2 | 0,034978 | 0,234978 |
| 0,694052 | 0,769692 | 4,86945 | 3,490204 | 16,94051754 | 1 | 3,490204 | 3,590204 |
| 0,696827 | 0,253113 | 4,816241 | 18,3189 | 16,96827016 | 1 | 18,3189 | 18,4189 |
| 0,163622 | 0,799583 | 24,13593 | 2,982198 | 11,63622278 | 2 | 2,982198 | 3,182198 |
| 0,441061 | 0,109059 | 10,91429 | 29,54484 | 14,41061093 | 1 | 25,3249 | 25,4249 |
| 0,431323 | 0,656771 | 11,21198 | 5,60559 | 14,3132266 | 1 | 5,60559 | 5,70559 |
| 0,48295 | 0,900227 | 9,704572 | 1,401447 | 14,82949639 | 1 | 1,401447 | 1,501447 |
| 0,892349 | 0,086992 | 1,518633 | 32,55911 | 18,92349466 | 1 | 20,44213 | 20,54213 |
| 0,924327 | 0,207261 | 1,049185 | 20,9837 | 19,24327491 | 1 | 20,29246 | 20,39246 |
| 0,376395 | 0,037901 | 13,02821 | 43,63688 | 13,7639502 | 1 | 26,79216 | 26,89216 |
| 0,390927 | 0,044951 | 12,52313 | 41,36253 | 13,90926838 | 1 | 26,4324 | 26,5324 |
| 0,996484 | 0,194519 | 0,046959 | 21,82965 | 19,96484248 | 1 | 20,0118 | 20,1118 |
| 0,331812 | 0,576174 | 14,70917 | 7,351277 | 13,31811552 | 1 | 7,351277 | 7,451277 |
| 0,047915 | 0,559439 | 40,51101 | 7,744279 | 10,47915047 | 3 | 7,744279 | 8,044279 |
 0,6421 0,6421 | 0,730159 | 5,906812 | 4,193241 | 16,42100193 | 1 | 4,193241 | 4,293241 |
| 0,114116 | 0,810873 | 28,94056 | 2,795257 | 11,14115709 | 2 | 2,795257 | 2,995257 |
| 0,352165 | 0,186655 | 13,91541 | 22,37991 | 13,52165029 | 1 | 22,37991 | 22,47991 |
| 0,991556 | 0,138274 | 0,113069 | 26,38029 | 19,91555662 | 1 | 20,02863 | 20,12863 |
| 0,770585 | 0,355898 | 3,474729 | 13,77483 | 17,7058547 | 1 | 13,77483 | 13,87483 |
| 0,924838 | 0,827546 | 1,041816 | 2,523867 | 19,24838474 | 1 | 2,523867 | 2,623867 |
| 0,992817 | 0,979257 | 0,096122 | 0,27948 | 19,92816761 | 1 | 0,27948 | 0,37948 |
| 0,97792 | 0,785261 | 0,297705 | 3,223196 | 19,77919545 | 1 | 3,223196 | 3,323196 |
| 0,757092 | 0,025213 | 3,710278 | 49,07171 | 17,57091712 | 1 | 21,2812 | 21,3812 |
| 0,085835 | 0,329045 | 32,73776 | 14,82079 | 10,85834688 | 3 | 14,82079 | 15,12079 |
| 0,705982 | 0,380758 | 4,6422 | 12,87455 | 17,05982381 | 1 | 12,87455 | 12,97455 |
| 0,26664 | 0,852119 | 17,62476 | 2,133723 | 12,66639658 | 2 | 2,133723 | 2,333723 |
| 0,465306 | 0,524926 | 10,20079 | 8,593314 | 14,65306242 | 1 | 8,593314 | 8,693314 |
| 0,472861 | 0,66851 | 9,986061 | 5,369392 | 14,72860649 | 1 | 5,369392 | 5,469392 |
| 0,680296 | 0,925811 | 5,136368 | 1,0278 | 16,80295806 | 1 | 1,0278 | 1,1278 |
| 0,044672 | 0,843099 | 41,44549 | 2,275606 | 10,44671844 | 3 | 2,275606 | 2,575606 |
| 0,710806 | 0,753522 | 4,551406 | 3,773286 | 17,10806221 | 1 | 3,773286 | 3,873286 |
| 0, 266693 | 0,070087 | 17,62209 | 35,44033 | 12,6669301 | 2 | 30,28902 | 30,48902 |
| 0,581376 | 0,857572 | 7,231438 | 2,048666 | 15,81375818 | 1 | 2,048666 | 2,148666 |
| 0,685254 | 0,821752 | 5,039546 | 2,617555 | 16,85253845 | 1 | 2,617555 | 2,717555 |
 0,019039 0,019039 | 0,186412 | 52,81682 | 22,39727 | 10,19039085 | 4 | 22,39727 | 22,79727 |
| 0,978664 | 0,795478 | 0,287554 | 3,050833 | 19,78664338 | 1 | 3,050833 | 3,150833 |
| 0,619496 | 0,576729 | 6,384651 | 7,33844 | 16,19496151 | 1 | 7,33844 | 7,43844 |
| 0,193785 | 0,411735 | 21,88009 | 11,83166 | 11,93784854 | 2 | 11,83166 | 12,03166 |
| 0,270723 | 0,343396 | 17,42213 | 14,25161 | 12,70722808 | 2 | 14,25161 | 14,45161 |
| 0,740137 | 0,341942 | 4,012275 | 14,3082 | 17,40136537 | 1 | 14,3082 | 14,4082 |
| 0,326512 | 0,23189 | 14,92384 | 19,48656 | 13,26512225 | 1 | 19,48656 | 19,58656 |
| 0,861257 | 0,635825 | 1,991501 | 6,037768 | 18,61256787 | 1 | 6,037768 | 6,137768 |
| 0,397221 | 0,427878 | 12,31017 | 11,31891 | 13,97220841 | 1 | 11,31891 | 11,41891 |
| 0,946734 | 0,952394 | 0,729825 | 0,65035 | 19,46734216 | 1 | 0,65035 | 0,75035 |
| 0,389553 | 0,877812 | 12,57006 | 1,737643 | 13,89553373 | 1 | 1,737643 | 1,837643 |
| 0,245971 | 0,354707 | 18,70055 | 13,8195 | 12,45971064 | 2 | 13,8195 | 14,0195 |
| 0,336868 | 0,411551 | 14,5075 | 11,83762 | 13,3686842 | 1 | 11,83762 | 11,93762 |
| 0,841433 | 0,784752 | 2,301979 | 3,231836 | 18,41433406 | 1 | 3,231836 | 3,331836 |
| 0,403454 | 0,942088 | 12,10258 | 0,795427 | 14,03453578 | 1 | 0,795427 | 0,895427 |
| 0,886946 | 0,618074 | 1,599621 | 6,415285 | 18,86945679 | 1 | 6,415285 | 6,515285 |
| 0,496647 | 0,65373 | 9,331667 | 5,66748 | 14,96647352 | 1 | 5,66748 | 5,76748 |
| 0,27751 | 0,367956 | 17,09199 | 13,33057 | 12,77509712 | 2 | 13,33057 | 13,53057 |
| 0,345784 | 0,309015 | 14,1592 | 15,65819 | 13,45784221 | 1 | 15,65819 | 15,75819 |
| 0,64179 | 0,747781 | 5,913248 | 3,875274 | 16,41790363 | 1 | 3,875274 | 3,975274 |
 0,538593 0,538593 | 0,678623 | 8,250603 | 5,1692 | 15,38592932 | 1 | 5,1692 | 5,2692 |
| 0,806912 | 0,751938 | 2,86054 | 3,801346 | 18,06912138 | 1 | 3,801346 | 3,901346 |
| 0,834306 | 0,221239 | 2,415405 | 20,11352 | 18,34305749 | 1 | 20,11352 | 20,21352 |
| 0,088644 | 0,722867 | 32,30841 | 4,32706 | 10,88643669 | 3 | 4,32706 | 4,62706 |
| 0,828376 | 0,843581 | 2,51051 | 2,267987 | 18,28375917 | 1 | 2,267987 | 2,367987 |
| 0,999488 | 0,831091 | 0,006824 | 2,466874 | 19,99488314 | 1 | 2,466874 | 2,566874 |
| 0,477209 | 0,931235 | 9,864022 | 0,949921 | 14,77208561 | 1 | 0,949921 | 1,049921 |
| 0,612596 | 0,23206 | 6,534002 | 19,47679 | 16,12595665 | 1 | 19,47679 | 19,57679 |
| 0,148279 | 0,673689 | 25,44876 | 5,266498 | 11,48279362 | 2 | 5,266498 | 5,466498 |
| 0,782451 | 0,697574 | 3,27099 | 4,80196 | 17,8245076 | 1 | 4,80196 | 4,90196 |
| 0,20137 | 0,685266 | 21,36814 | 5,0393 | 12,01370218 | 2 | 5,0393 | 5,2393 |
| 0,869146 | 0,298105 | 1,869926 | 16,13748 | 18,6914576 | 1 | 16,13748 | 16,23748 |
| 0,379341 | 0,224428 | 12,92427 | 19,92266 | 13,79340735 | 1 | 19,92266 | 20,02266 |
| 0,975016 | 0,782984 | 0,337348 | 3,261915 | 19,75016296 | 1 | 3,261915 | 3,361915 |
| 0,544761 | 0,678805 | 8,098786 | 5,165617 | 15,4476055 | 1 | 5,165617 | 5,265617 |
| 0,45267 | 0,689587 | 10,5679 | 4,955491 | 14,52669778 | 1 | 4,955491 | 5,055491 |
| 0,560808 | 0,024921 | 7,711679 | 49,22705 | 15,60808421 | 1 | 23,31976 | 23,41976 |
| 0,625022 | 0,792089 | 6,26625 | 3,107751 | 16,25021778 | 1 | 3,107751 | 3,207751 |
| 0,030501 | 0,379762 | 46,53348 | 12,90946 | 10,30500545 | 3 | 12,90946 | 13,20946 |
| 0,357271 | 0,210818 | 13,72346 | 20,75683 | 13,57271424 | 1 | 20,75683 | 20,85683 |
| 0,749104 | 0,111259 | 3,851703 | 29,27854 | 17,49103812 | 1 | 21,34274 | 21,44274 |
| 0,998746 | 0,767691 | 0,016735 | 3,52491 | 19,98745654 | 1 | 3,52491 | 3,62491 |
| 0,818165 | 0,426389 | 2,675881 | 11,36537 | 18,1816514 | 1 | 11,36537 | 11,46537 |
| 0,385981 | 0,693783 | 12,69289 | 4,874618 | 13,85981273 | 1 | 4,874618 | 4,974618 |
| 0,575407 | 0,997278 | 7,369035 | 0,036348 | 15,75407038 | 1 | 0,036348 | 0,136348 |
| 0,548384 | 0,369792 | 8,010386 | 13,2642 | 15,48384322 | 1 | 13,2642 | 13,3642 |
| 0,785698 | 0,815224 | 3,215773 | 2,7239 | 17,85697871 | 1 | 2,7239 | 2,8239 |
| 0,545663 | 0,195207 | 8,076713 | 21,78257 | 15,45663119 | 1 | 21,78257 | 21,88257 |
| 0,783897 | 0,932456 | 3,246372 | 0,932445 | 17,83896817 | 1 | 0,932445 | 1,032445 |
| 0,669346 | 0,366031 | 5,352723 | 13,4005 | 16,69345952 | 1 | 13,4005 | 13,5005 |
| 0,267188 | 0,785062 | 17,59737 | 3,226564 | 12,67188097 | 2 | 3,226564 | 3,426564 |
| 0,343286 | 0,402036 | 14,25588 | 12,14952 | 13,43286189 | 1 | 12,14952 | 12,24952 |
| 0,42829 | 0,5392 | 11,30607 | 8,235585 | 14,28289844 | 1 | 8,235585 | 8,335585 |
| 0,374801 | 0,708142 | 13,0848 | 4,601467 | 13,74801022 | 1 | 4,601467 | 4,701467 |
| 0,015266 | 0,481739 | 55,76145 | 9,738033 | 10,15266281 | 4 | 9,738033 | 10,13803 |
| 0,715998 | 0,191632 | 4,454363 | 22,02903 | 17,15998477 | 1 | 21,61435 | 21,71435 |
| 0,525342 | 0,340852 | 8,582743 | 14,35077 | 15,25342052 | 1 | 14,35077 | 14,45077 |
| 0,932104 | 0,447599 | 0,937478 | 10,71809 | 19,32104034 | 1 | 10,71809 | 10,81809 |
| 0,230697 | 0,528953 | 19,55534 | 8,491398 | 12,30696995 | 2 | 8,491398 | 8,691398 |
| 0,467633 | 0,165675 | 10,13429 | 23,96968 | 14,67632816 | 1 | 23,96968 | 24,06968 |

 В ячейки первой строки A1, B1,..,H1 помещаются заголовки таблицы. В ячейки A2 и В2 помещаются РРСЧ в соответствии с формулами А2=СЛЧИС(), В2=СЛЧИС().
В ячейки первой строки A1, B1,..,H1 помещаются заголовки таблицы. В ячейки A2 и В2 помещаются РРСЧ в соответствии с формулами А2=СЛЧИС(), В2=СЛЧИС().В ячейки C2, D2, E2 помещаются значения случайных величин X1, X2, X3, первые две которые имеют равномерное распределение, а третья - распределение Эрланга в соответствии с формулами разыгрывания.
С2 = ЕХР(2 + 1,4*КОРЕНЬ(-2*LN(В2))*COS(2*ПИ()*А2),
D2 = ЕХР(2 + 1,4*KOPEHb(-2*LN(B2))*COS(2*ПИ()*А2),
Е2 = - (LN(A2) + LN (В2) )/0, 05.
В ячейку F2 помещается значение дискретной случайной величины V, подчиненной распределению геометрическому распределению вероятностей с параметром 0,7:
F2 = ЦЕЛОЕ(LN(А2)/LN(1 - 0,7)) + 1.
Рассмотрим структурную схему, изображенную на рисунке 1. При отказе элемента X3 наступает отказ системы. При отказе элемента X1 в работу включается элемент X2, но это событие не является отказом системы. Система откажет, если после этого произойдет отказ элемента X3 или X2. Время до отказа этой системы равно наименьшему из времени совместной работы элементов X1 и X2 или X3, т.е Y = МИН(X1+X2;X3).
По этому в ячейку G2 помещается формула, расчет по которой даст значение случайной величины Y:
G2 = МИН(С2+D2;E2),
В ячейку Н2 помещается формула для расчета случайной величины Z:
H2 = G2/1+0.1*F2.
В результате этих действий будут заполнены ячейки второй строки А2, В2,..,H2. По заданию необходимо получить 100 значений данных случайных величин. Поэтому содержимое ячеек А2, В2,..,H2 копируется в следующие строки, вплоть до 101 строки (таблица 2).
 Также следует отметить, что при вводе какой-либо информации на лист Excel содержимое ячеек А2:Н101 будет изменяться. Чтобы этого не происходило, целесообразно выполнить следующие действия:
Также следует отметить, что при вводе какой-либо информации на лист Excel содержимое ячеек А2:Н101 будет изменяться. Чтобы этого не происходило, целесообразно выполнить следующие действия: □ выделить указанный блок ячеек и скопировать его в буфер
(
□ загрузить Microsoft Word и вставить содержимое буфера в документ
Word (
□ выделить содержимое таблицы Word и скопировать его в буфер
(
□ перейти на новый лист Microsoft Excel и вставить содержимое буфера
в документ Excel (
Вывод:
В этой части мы рассмотрели в каком случае откажет структурная схема системы, а также с помощью законов распределения получили таблицу случайных чисел.
 Статистическая обработка
Статистическая обработка
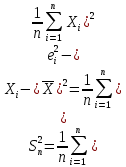
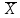
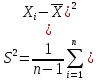 (13)
(13) Согласно схеме, сначала работают элементы 1 и 2, а элемент 3 находится в резерве. При отказе элемента X1 или X2 в работу включается элемент X3, но это событие не является отказом системы. Система откажет, если после этого произойдет отказ элемента X2 и X3.
Согласно схеме, сначала работают элементы 1 и 2, а элемент 3 находится в резерве. При отказе элемента X1 или X2 в работу включается элемент X3, но это событие не является отказом системы. Система откажет, если после этого произойдет отказ элемента X2 и X3.