Курсовая работа. Готовая курсовая работа. Установление закона распределения времени безотказной работы системы по известным законам распределения элементов
 Скачать 0.56 Mb.
|
|
Подбор подходящего закона распределения вероятностей При достаточно большом объеме выборки статистические данные позволяют подобрать подходящее распределение вероятностей. С этой целью можно рассмотреть некоторые известные распределения, например равномерное, нормальное и гамма-распределение. Предположим, что случайная величина X имеет функцию распределения F(x). Будем называть это предположение гипотезой о виде распределения случайной величины X. Чтобы иметь полную информацию о распределении случайной величины, надо знать параметры этого распределения или их некоторые оценки. Как правило, параметры распределений берутся такими, чтобы математическое ожидание случайной величины X было равно выборочной средней, а среднее квадратическое отклонение случайной величины X - выборочному среднему квадратическому отклонению. Указанные выборочные характеристики находятся в ячейках G12 и G14 соответственно. Откроем новый лист Excel и поместим эти значения в ячейки А2 и В2 соответственно (таблица 5). Определим параметры равномерного, нормального и гамма-распределений в соответствии с формулами:  (21) (22) (23) (24)и запишем их в ячейки: B5= А2 - В2·КОРЕНЬ(3), B6= А2 + В2·КОРЕНЬ(3), B8= А2, B9= В2, B11= (А2/В2)^2, B12= В2^2/А2. Далее построим таблицу, шапка которой располагается в ячейках А14:  В ячейках А15: А24 содержатся середины частичных интервалов,взятые из ячеек D26: D35 предыдущего листа. В ячейках В15: В24 вычислены плотности относительных частот как частное от деления относительных частот предыдущего листа (ячейки F26: F35) на шаг (ячейка $F$23).
Плотности равномерного, нормального и гамма-распределения  рассчитываются в соответствии с формулами: , , ,затем они копируются в блок ячеек С16:Е24. Построим гистограмму частот, совмещенную с плотностью каждого из указанных ранее распределений. Гистограмма частот - это графическое изображение зависимости плотности относительных частот ni / nh от соответствующего интервала группировки. В этом случае площадь гистограммы равна единице, и гистограмма может служить аналогом плотности распределения вероятностей случайной величины X. Графическое изображение гистограммы и кривых различных распределений приведено на рисунках 4,5. При этом используется нестандартная диаграмма типа "График | гистограмма". 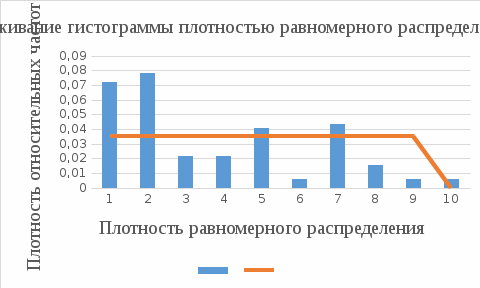 Рисунок 4 - Сглаживание гистограммы плотностью равномерного распределения  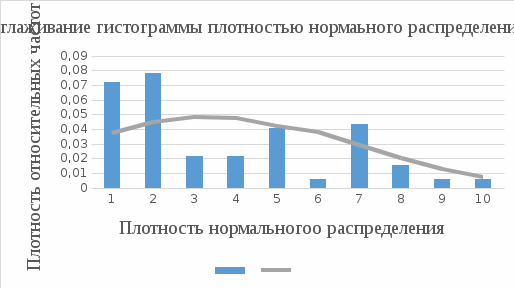 Рисунок 5 - Сглаживание гистограммы плотностью нормального распределения По внешнему виду этих графиков вполне можно судить о соответствии кривой распределения данной гистограмме, т. е. о том, какая кривая ближе к полученной гистограмме. Используя критерий 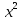 , надо установить, верна ли принятая нами гипотеза о распределении случайной величины X, т. е. о соответствии функции распределения F(x) экспериментальным данным, чтобы ошибка не превышала заданного уровня значимости  (вероятность того, что будет отвергнута правильная гипотеза). 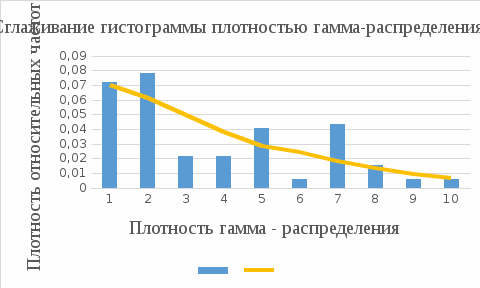Рисунок 6 - Сглаживание гистограммы плотностью гамма-распределения  Для применения критерия 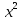необходимо, чтобы частоты ni, соответствующие каждому интервалу, были не меньше 5. Если это не так, рядом стоящие интервалы объединяются, а их частоты суммируются. В результате общее количество интервалов может уменьшиться до значения  . Далее вычисляется следующая сумма:  (25)где рi - теоретическая вероятность того, что случайная величина X примет значение из интервала [ai-1, аi]. Мы предположили, что случайная величина X имеет функцию распределения F(x), поэтому pt =F(ai)-F(ai-1). Образец расчетов по формуле (2) в Excel для трех распределений показан в таблице 6.  В колонке А содержатся левые, а в колонке В - правые границы интервалов. В колонке С находятся соответствующие частоты. Заметим, что интервалы с 5-го по 10-й объединены в один, чтобы все частоты были не менее пяти. Количество интервалов вместо k = 10 стало равным k' = 5. В колонке D рассчитываются теоретические вероятности в зависимости от вида распределения. Как обычно, вычисляется одно значение, которое копируется в другие ячейки:для равномерного распределения: D45= ЕСЛИ(В45 < $В$5; 0; ЕСЛИ(В45 <= $В$6; (В45 - $В$5)/($В$6 - $В$5); 1)) - ЕСЛИ(А45 < $В$5; 0, ЕСЛИ(А45 <= $В$6; (А45 - $В$5)/($В$6 - $В$5); 1)). для нормального распределения: D52 = НОРМРАСП(В53; $В$8; $В$9; ИСТИНА) - НОРМРАСП(А53; $В$8; $В$9; ИСТИНА). для гамма-распределения: D59=ГАММАРАСП(В61; $В$11; $В$12; ИСТИНА) - ГАММАРАСП(А61; $В$11; $В$12; ИСТИНА). Таблица 6. Подбор распределения на основе критерия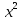
 В колонке Е рассчитываются слагаемые соотношения (2) по формуле: Е45 = (С45 - 100·D45)^2/(100·D45), которая копируется в другие ячейки колонки Е. Согласно (2) для каждого рассмотренного распределения определяются итоговые суммы: Е50 = СУММ(Е45:Е49), Е57 = СУММ(Е52:Е56), Е64 = СУММ(Е61:Е66), которые равны соответственно 96,29327538, 87,44402859 и 96,92233357. 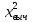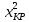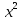Гипотеза о виде закона распределения должна быть принята, если вычисленное значение  достаточно мало, а именно не превосходит  критического значения  которое определяется по распределению в зависимости от заданного уровня значимости  и числа степеней свободы  . Здесь s - число неизвестных параметров распределения, которые были определены по выборке (для равномерного, нормального и гамма-распределения s = 2). В данном примере r = k'-s-1 = 5-3 = 2. 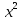Полагая = 0,05, критическое значение критерия в Excel рассчитывается по формуле: Е66 = ХИ2ОБР(0,05;2) Поскольку 87,44402859 > 5,991, то принимается гипотеза о том, что статистические данные имеют нормальное распределение с параметрам m=21.936 и σ =1.402 соответственно. Вывод: В этой части я рассмотрел равномерное, нормальное и гамма-распределение и составил по ним графики. Далее я подбирал распределения на основе критерия 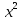. Определение характеристик надёжности системыВ разделе 3 было установлено, что случайная величина Z принадлежит множеству Г(10,27049;8,229049) с плотностью распределения вероятностей: 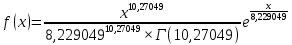 (26)Основными характеристиками надежности невосстанавливаемой системы являются среднее время безотказной работы и вероятность безотказной работы в течение времени t. Среднее время безотказной работы системы T1 равно математическому ожиданию m, т. е. T1 = 10,27049 час. Вероятность безотказной работы вычисляется по формуле:  (27)Построим график функции 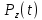 , используя Excel. В ячейках А71: А91 запишем значения аргумента t, изменяющегося от 0 до 20 часов с шагом 1 час.Так как случайная величина Z имеет нормальное распределение, то в ячейку В71 записывается формула: В71 = 1 – НОРМРАСП (А71; $В$8; $В$9; ИСТИНА), которая затем копируется в ячейки В72: В98 (таблица 7). При этом используется аргумент истина, который, согласно равенству (3), соответствует интегральной функции распределения (а не плотности распределения). В результате будет получена таблица значений вероятности безотказной работы 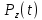, график которой представлен на рисунке 7.Таблица 7 - Значения вероятности безотказной работы системы
 По таблице 3 и графику функции 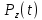(рисунок 7) можно определить вероятность того, что система безотказно проработает в течение заданного времени.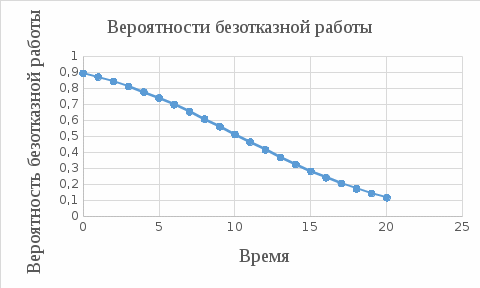 Рисунок 7 - График вероятности безотказной работы системы  Вывод: В это части я произвёл определение характеристик надёжности систем. Рассчитал значения вероятности безотказной работы системы и построил график вероятности безотказной работы. Заключение  В данной курсовой работе изучили методы статистического моделирования применительно к задачам нахождения законов распределения времени безотказной работы и показателей надежности технических систем с использованием прикладных программных средств.Оценили надежность системы S методом статистического моделирования на ЭВМ. Разработали алгоритмы разыгрывания случайных величин Х1, Х2, Х3 и V с использованием генераторов случайных чисел, содержащихся в Microsoft Excel. Определили время безотказной работы системы Y в зависимости от времени безотказной работы Х1, Х2, Х3 элементов на основе структурной схемы расчета надежности. Определили время безотказной работы системы с учетом влияния внешней среды Z. Построили моделирующий алгоритм, имитирующий работу системы S и учитывающий возможность отказа элементов и случайные воздействия внешней среды E. Реализовали полученный алгоритм на ЭВМ. Выполнили статистическую обработку полученных результатов. Для каждой случайной величины рассчитали основные статистические характеристики: выборочное среднее, выборочную дисперсию, выборочное среднее квадратическое отклонение, наименьшее и наибольшее значения, размах выборки, асимметрию, эксцесс. Сформировали статистический ряд, содержащий границы и середины частичных интервалов, а также соответствующие частоты; вычислили относительные, накопленные и накопленные относительные частоты. Для величины Z построили полигон и кумуляту частот. Рассмотрели три непрерывных распределения(равномерное, нормальное, гамма-), изобразили на гистограмме для Z плотности этих распределений.  С помощью критерия 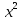выполнили проверку справедливости гипотезы о соответствии статистических данных выбранным распределениям, в данном случае статические данные имеют нормальное распределение.Определили плотность распределения, математическое ожидание, дисперсию и среднее квадратическое отклонение времени безотказной работы Z системы. Определили основные характеристики надежности системы. Литература  1 Зорин В.А., Бочаров B.C. Надежность машин: Учебник. - Орел: Изд. ОрелГТУ,2010. - 549с.Шарыпов А.В., Осипов Г.В. Основы теории надежности транспортных систем: Учебное пособие. - Курган: Изд-во Курганского гос. ун-та, 2006.- 128 с. Половко А.М.,Гуров С.В. Основы теории надежности. - СПб.: БХВ-Петербург, 2009. - 704 с. Половко А.М.,Гуров С.В. Основы теории надежности. Практикум. - СПб.: БХВ-Петербург, 2006. - 560 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||