Курсовая работа. Готовая курсовая работа. Установление закона распределения времени безотказной работы системы по известным законам распределения элементов
 Скачать 0.56 Mb.
|
|
Вычисление основных характеристик выборки Основными числовыми характеристиками выборочной совокупности являются: выборочное среднее, выборочная дисперсия, выборочное среднее квадратическое (или стандартное) отклонение, наименьшее и наибольшее значения, размах выборки, асимметрия, эксцесс. Для расчета указанных характеристик в Excel необходимо поставить курсор в ячейку, в которую будет записано значение характеристики, вызвать соответствующую функцию и в качестве ее аргумента указать блок ячеек со статистическими данными. Для удобства следующих операций значения случайной величины Z (статистические данные) перепишем на другой лист в прямоугольный блок ячеек, например в ячейки Al: J10. Значения вычисляемых характеристик будем располагать в ячейках с G12 по G19, как показано в таблице 3. Таблица 3 – Расчёт выборочных характеристик
Вычисление выборочных характеристик осуществляется по формулам:  выборочное среднее: G12 = СРЗНАЧ (А1: J10),выборочная дисперсия: G13 = ДИСП (Al: J10), выборочное среднее квадратическое отклонение: G14= СТАНДОТКЛОН(Al: J10) ИЛИ G14 = КОРЕНЬ(G13), наименьшее значение: G15 = МИН(А1: J10), наибольшее значение: G16 = МАКС (Al: J10), размах выборки: G17 = G16 - G15, асимметрия: G18 = СКОС (Al: J10), эксцесс: G19 = ЭКСЦЕСС (Al: J10). Вывод: В это части КП я рассмотрел основные числовые характеристики и произвёл вычисление выборочных характеристик с помощью некоторых формул. Полученные значения внёс в таблицу 3. Формирование статистического ряда и представление данных Для наглядного представления статистических данных используется группировка. Числовая ось разбивается на интервалы, и для каждого интервала подсчитывается число элементов выборки, которые в него попали. Группировка данных производится в следующей последовательности: -наименьшее значение округляется в меньшую сторону, а наибольшее - в большую сторону до "хороших" чисел хmin и хmax; - выбирается количество групп k, удовлетворяющее неравенству 6 < k < 20; иногда оно определяется по формуле 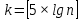 (14)Например, если объем выборки n = 100, то k = 10; -находится шаг по формуле 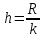 (15)где R = хmах - хmin - длина промежутка, в котором содержатся статистические данные; -определяются границы частичных интервалов:  ,  ,  ,...  ; (16)-в каждом интервале вычисляются средние значения  (17)-для каждого интервала  , i = 1, 2,...,k находятся:а) частоты пi, т. е. число выборочных значений, попавших в интервал; б) относительные частоты 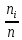 (18)в) накопленные частоты 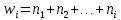 (19)г) накопленные относительные частоты   (20)Для выборочной совокупности (таблица 3) результаты группировки в Excel представлены в таблице 4. Сначала следует указать объем выборки, максимальное и минимальное значения, размах выборки, количество групп и шаг: А23 = 100, В23 = 100, С23 = 0, D23 = В23 - С23, Е23 = 10, F23 = D23 / Е23. В ячейках А25: Н25 указываются заголовки таблицы. В этой таблице колонки В и С можно заполнить в соответствии с формулами (1) или заполнить две строки и скопировать их в последующие так, чтобы всего получилось k = 10 строк. Колонку D можно заполнить, используя формулу: D26 = (В26 + С26) / 2 надежность система статистический моделирование с последующим копированием в ячейки D27: D35. Таблица 4 - Группировка статистических данных
 Для заполнения колонки Е следует выделить ячейки Е26: Е35 и обратиться к функции ЧАСТОТА, указав массив статистических данных и массив правых границ интервалов:{= ЧАСТОТА (А1:J10; С26:С35)}. Одновременное нажатие клавиш Заполнение колонки F производится по формуле: Е26 / $А$23 с последующим копированием в ячейки F27: F35. Далее заполняются две ячейки колонки G по формулам: G26 = Е26, G27 = G26 + Е27 С последующим копированием G27 в ячейки G28: G35. Колонка Н заполняется по формуле: Н26 = G26 / $А$23 с последующим копированием в ячейки Н27: Н35.  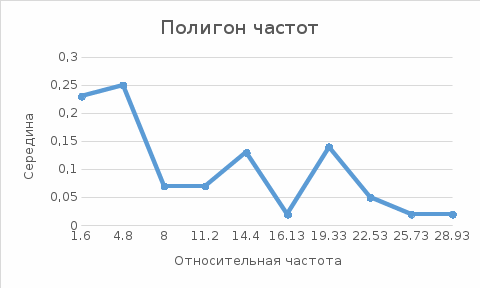 Рисунок 2 - Полигон частот 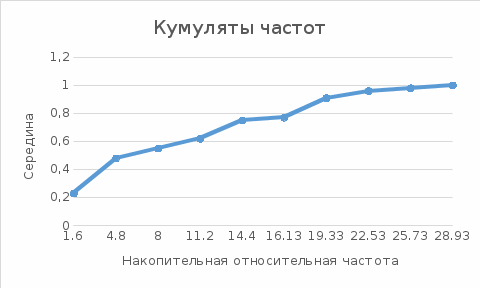 Рисунок 3 - Кумулята частот Данные, собранные в таблице 4 нуждаются в наглядном представлении. Формами такого наглядного представления являются: -полигоны частот - графическая зависимость частот (относительных частот) от середин интервалов (рисунок 2); -кумуляты частот - графическая зависимость накопленных частот (накопленных относительных частот) от середин интервалов (рис.3). Вывод: В этой части, чтобы наглядно представить статистические данные используется группировка. С помощью группировки я получил два графика Полигон частот и Кумулята частот.  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||