Сергеев - Метрология. В. Г. Фирстов Кандидат физикоматематических наук

• Название: В. Г. Фирстов Кандидат физикоматематических наук
• Анкор: Сергеев - Метрология.doc
• Дата: 28.01.2017
• Размер: 4.38 Mb.
• Имя файла: Сергеев - Метрология.doc
• Тип: Документы; #707
• страница: 17 из 37

Глава 9. СУММИРОВАНИЕ ПОГРЕШНОСТЕЙ

9.1. Основы теории суммирования погрешностей

Определение расчетным путем оценки результирующей погрешности по известным оценкам ее составляющих называется суммированием погрешностей.

Главной проблемой, возникающей при суммировании, является то, что все составляющие погрешности должны рассматриваться как случайные величины. С точки зрения теории вероятностей они наиболее полно могут быть описаны своими законами распределения, а их совместное действие — соответствующим многомерным распределением. Однако в такой постановке задача суммирования погрешностей практически не разрешима уже для нескольких составляющих, не говоря о нескольких десятках.

Практически приемлемый путь решения данной задачи суммирования погрешностей состоит в отказе от определения и использования многомерных функций распределения составляющих погрешности. Необходимо подобрать для характеристик составляющих такие числовые оценки (СКО, эксцесс и др.), оперируя с которыми можно было бы получить соответствующие числовые оценки результирующей погрешности. При этом следует учитывать, что:

• отдельные составляющие погрешности могут быть коррелиро-ваны между собой;

• при суммировании случайных величин их законы распределения существенно деформируются, т.е. форма закона суммы может резко отличаться от формы закона распределения составляющих.

Правила суммирования погрешностей основываются [4] на том, что погрешность по абсолютному значению всегда много меньше самой измеряемой величины. Поэтому изменение погрешности в зависимости от изменения измеряемой величины может быть учтено, если все суммируемые случайные и систематические составляющие погрешности разделить на аддитивные и мультипликативные. Сумма аддитивных составляющих даст значение аддитивной части результирующей погрешности, а сумма мультипликативных составляющих — значение мультипликативной части результирующей погрешности.

В пределах некоторого диапазона изменения, как правило, десятикратного, измеряемой величины изменение результирующей погрешности может быть с достаточной степенью точности представлено прямой линией или простейшей кривой (парабола, гипербола). Это дает возможность описать результирующую погрешность линейной или нелинейной двузвенной формулой. При большем изменении измеряемой величины весь диапазон разбивается на участки, для которых и определяются крайние погрешности.
Пример 9.1. Основная допускаемая погрешность измерения сопротивления цифрового микропроцессорного измерителя иммитанса марки Е7-14 при различных диапазонах измерения и добротностях Q приведена в таблице.

Диапазон измерения	Конечное значение диапазона Rk, Ом	Предел допустимого значения основной погрешности, Ом
0,1. ..1000 мОм	1	10-3(1+Q) R+310 -4Rk
0,001. ..10 Ом	10	10-3 (l+Q) R+210-4Rk
0,01. ..100 Ом	100	10-3 (1+Q) R+210-4Rk
100.. .1000 Ом	1000	[10-3 (l+Q)+210-3 R/Rk] R
1...10 кОм	10000	[10-3(l + Q)+210-3 R/Rk] R

Для устранения влияния деформации формы законов распределения все суммируемые составляющие исходно представляются своими СКО и все операции расчетного суммирования проводятся только над ними. Учет взаимных корреляционных связей между суммируемыми составляющими производится путем использования различных правил суммирования для жестко и слабо коррелированных составляющих. Эти правила рассмотрены далее.

В результате суммирования СКО составляющих получаются средние квадратические отклонения соответственно аддитивной, мультипликативной или нелинейной составляющих результирующей погрешности. СКО аддитивной составляющей результирующей погрешности будет характеризовать результирующую погрешность в начале диапазона. Сумма СКО аддитивной и мультипликативной составляющих в конце диапазона описывает результирующую погрешность в конце диапазона. Если участков несколько, то суммирование проводится на всех участках, а затем принимается решение о методе описания результирующей погрешности.

Результирующую погрешность необходимо выразить в виде доверительного интервала. Его расчет по полученному СКО является с точки зрения теории самой трудной операцией при суммировании погрешностей. Это связано с тем, что доверительный интервал равен произведению рассчитанного СКО и множителя, зависящего от закона распределения результирующей погрешности. В то же время вся излагаемая методика с самого начала была нацелена на то, чтобы обойтись без точного определения результирующего закона распределения суммы всех составляющих.

Практические правила расчетного суммирования результирующей погрешности состоят в следующем [4]:

1. Для определения суммарного значения СКО должны учитываться корреляционные связи различных составляющих погрешности. В связи с этим исходными данными для более точного расчета должны служить оценки именно всех отдельных составляющих погрешности, а не оценки некоторых суммарных погрешностей.

2. Для каждой составляющей должно быть найдено ее СКО. В большинстве случаев для этого необходимо знание или предположение о виде закона ее распределения.

3. Все суммируемые составляющие разделяются на аддитивные и мультипликативные составляющие, которые суммируются отдельно.

4. Так как в большинстве случаев точное значение коэффициента корреляции р найти невозможно, то все погрешности должны быть условно разделены на:

• сильно коррелированные при 0,7  |ρ|  1, для которых считают ρ -= ±1 в зависимости от знака коэффициента корреляции;

• слабо коррелированные при 0 |ρ|  0,7, для которых ρ = 0.

5. Из суммируемых составляющих выделяются группы сильно коррелированных между собой погрешностей и внутри этих групп производится алгебраическое суммирование их оценок.

6. После алгебраического суммирования групп сильно коррелированных погрешностей суммарные по группам и оставшиеся вне групп погрешности можно считать некоррелированными и складывать по правилу геометрического суммирования.

Для определения СКО суммарной погрешности при начальном значении измеряемой величины складывают лишь аддитивные составляющие, а для определения СКО погрешности в конце диапазона изменения измеряемой величины — все просуммированные выше составляющие.

7. Для перехода от СКО погрешности к доверительному значению должно быть вынесено суждение о форме закона распределения результирующей погрешности и тем самым выбрано значение квантильного множителя.

Изложенная методика может быть несколько упрощена. Самым сложным в ней являются нахождение СКО всех составляющих по известным их интервальным оценкам и определение интервальной оценки результирующей погрешности по полученному СКО.

В обоих случаях необходимо знание закона распределения погрешностей. Упрощение методики суммирования состоит в том, чтобы сделать эти переходы по возможности более простыми. Один из вариантов состоит в следующем. Согласно центральной предельной теореме, если число суммируемых независимых составляющих достаточно велико (практически при m > 5) и если среди этих составляющих нет существенно преобладающих над остальными, то результирующий закон распределения близок к нормальному. Однако предположение о близости закона распределения к нормальному без соответствующего анализа достаточно рискованно даже и при большом числе суммируемых составляющих. Тем не менее при недостатке времени и невысоких требованиях к точности получаемого результата предположение о нормальности закона распределения результирующей погрешности вполне возможно. В этом случае доверительный интервал  = z_pS_, где z_p — квантильный множитель, определяемый через функцию Лапласа; S_ — суммарное СКО или его оценка.

Такой прием существенно снижает трудоемкость расчетов, но может вносить весьма значительные ошибки, если реальное распределение сильно отличается от нормального закона. Например, при фактическом арксинусоидальном распределении ошибка может достигать 180% [4]. Поэтому использовать его надо весьма осмотрительно.

В качестве другого пути упрощения перехода от СКО результирующей погрешности к ее интервальной оценке следует указать возможность использования доверительной вероятности Р_д = 0,9, при которой для большой группы различных распределений имеет место соотношение

(9.1)

Действительно, как показано в [4], для широкого класса симметричных, высокоэнтропийных (k > 1,7) распределений, а именно для равномерного, треугольного, трапецеидальных, нормального, экспоненциальных с показателем степени   2/3, двухмодальных с глубиной антимодальности менее 1,5, интегральные кривые F(x) в области 0,05 и 0,95 квантилей пересекаются между собой в очень узком интервале значений X/S = 1,6 ± 0,05. Поэтому с погрешностью 0,058 можно считать, что квантили 0,05 и 0,95 для любых из этих распределений могут быть найдены как+ 1,6 S, где Х_ц— координата центра распределения; ST— его СКО. Отсюда следует, что значение доверительного интервала, найденное по формуле (9.1), для любого из названных распределений является интервалом с 90%-ной доверительной вероятностью.

При Р_д > 0,9 интегральные кривые для разных законов распределения резко расходятся между собой. В этом случае для нахождения доверительного интервала  = z_pS_ в [4] предложено вместо большого числа таблиц квантилей разнообразных распределений найти для близких классов распределений аппроксимирующие выражения z_p = f(,P), где  — эксцесс распределения.

Для входящих в классы экспоненциальных и трапецеидальных распределений, а именно: распределения Лапласа ( = 6); нормального распределения ( = 3); трапецеидального распределения с соотношением верхнего и нижнего оснований 1:2 ( = 2) и равномерного распределения ( = 1,8), зависимость квантильного множителя от эксцесса и доверительной вероятности аппроксимируется уравнением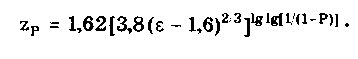

(9.2)

Погрешность аппроксимации не превышает 4% при изменении Р от 0,9 до 0,99 и 8% — от 0,9 до 0,999.

Для кругловершинных двухмодальных распределений, представляющих собой композицию нормального и дискретного двузначного распределений, в диапазоне изменения е от 3 до 1,3 для Р от 0,9 до 0,999 с погрешностью 10% зависимость z_p = f(,P) аппроксимируется выражением

(9.3)

Для островершинных двухмодальных распределений, образующихся как композиция распределения Лапласа и дискретного двузначного распределения, рассматриваемая зависимость в интервале значений е от 1,8 до 6 при Р от 0,9 до 0,999 с погрешностью 5% аппроксимируется формулой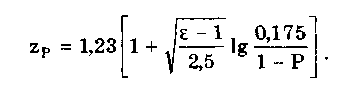

(9.4)

Для уплощенных распределений, образующихся как композиция экспоненциального распределения с  = 1/2 и равномерного распределения в интервале значений  от 6 до 1,8 с погрешностью 8%, рассматриваемая зависимость аппроксимируется формулой

(9.5)

Использование приведенных уравнений позволяет, не прибегая к таблицам, с достаточной для практики степенью точности вычислять доверительные интервалы для всех встречающихся распределений погрешностей. Однако для выбора формулы нужно вынести суждение о классе распределения суммарной погрешности.

Дальнейшие упрощения методики, выражающиеся в пренебрежении разделением погрешностей на аддитивные и мультипликативные, коррелированные и некоррелированные, недопустимы, поскольку при суммировании погрешностей получены неверные результаты.

9.2. Суммирование систематических

погрешностей

При определении границ систематическая погрешность оценивается по ее составляющим, называемым элементарными систематическими погрешностями. Если для части составляющих находят их оценки и эти погрешности устраняют введением поправок, то в качестве рассматриваемых элементарных погрешностей выступают погрешности определения поправок, которые также характеризуются границами.

Множество возможных способов измерений данной величины дает множество различных реализаций каждой элементарной систематической погрешности. Поэтому последние можно рассматривать как случайные величины и суммировать методами, разработанными в математической статистике. Однако поскольку их функции распределения, как правило, неизвестны, то при суммировании видом распределения задаются, исходя из известных данных об элементарной систематической погрешности. Это не вносит существенной ошибки в получаемые результаты, так как в соответствии с принципом оценивания погрешностей сверху из всех возможных ее распределений всякий раз выбирают наихудшее. Получаемая оценка погрешности надежно характеризует неопределенность результата.

При выборе закона распределения необходимо руководствоваться следующими правилами:

• если известна оценка границ погрешности + 8;, то ее распределение следует считать равномерным (такая ситуация наиболее часто встречается в практике);

• если известна оценка СКО, то распределение следует считать нормальным.

Применение этого правила позволяет статистически суммировать элементарные систематические погрешности и обычно приводит к осторожным и вместе с тем не слишком завышенным оценкам погрешности результата измерений.

При равномерном законе распределения элементарных систематических погрешностей их сумма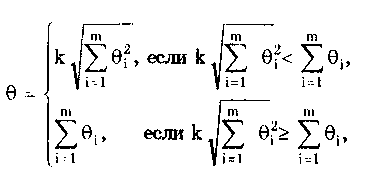

(9.6)

где _i — границы i-й элементарной случайной погрешности; k —поправочный коэффициент, зависящий от числа слагаемых т, их соотношения и доверительной вероятности. При Р < 0,99 он мало зависит от числа слагаемых и может быть представлен усредненными значениями, приведенными в табл. 9.1. Их погрешность не превышает 10% [3]. При Р > 0,99 коэффициент k существенно зависит от числа слагаемых и соотношения между ними. Поэтому при m > 4 рекомендуется принимать среднее значение k = 1,4, а при m < 4 значение k необходимо уточнить по ГОСТ 8.207—76 или табл. 9.2. Параметр С, характеризующий отношение границ составляющих систематической погрешности Q_m/Q_m-1, принимается равным наименьшему значению указанного отношения при условии, что ₁ < ₂ < ₃ < ₄.

Таблица 9.1

Зависимость коэффициента k от Р и m

р	Значение k при m равном					Среднее значение
	2	3	4	5	00
0,90	0,97	0,96	0,95	0,95	0,95	0,95
0,95	1,10	1,12	1.12	1,12	1,13	1,1
0,99	1,27	1,37	1,41	1,42	1,49	1,4

Таблица 9.2

Зависимость коэффициента k от m и С при Р = 0,99

	Значение k при m, равном
m	0	0,5	1	2	3	4	5	6	7
2	0,98	1,15	1,27	1,22	1,15	1,12	1,08	1,07	1,05
3	1,27	1,32	1,37	1,32	1,24	1,18	1,15	1,12	1,08
4	1,38	1,40	1,41	1,36	1,28	1,23	1,18	1,15	1,11

При большом числе слагаемых результирующая погрешность имеет практически нормальное распределение. Оценка дисперсии этого распределения равна сумме дисперсий слагаемых:

Задавшись доверительной вероятностью, получим  как границу доверительного интервала  = z_pS_, где z_p — квантиль нормального распределения при выбранном уровне значимости q = 1- Р.

9.3. Суммирование случайных погрешностей

Правила суммирования случайных погрешностей основаны на известных из теории вероятностей положениях [48,49]:

а) оценка математического ожидания результирующей погрешности определяется алгебраической суммой оценок математических ожиданий составляющих;

б) оценка СКО суммарной погрешности определяется выражением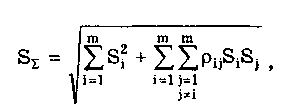

(9.7)

где S_i — оценка СКО i-й составляющей погрешности; m — число суммируемых составляющих погрешностей; ρ_ij — коэффициент корреляции между i- и j-й составляющими.

При суммировании m случайных погрешностей их коэффициенты корреляции образуют матрицу, которая ввиду равенства ρ_ij = ρ_ij является диагональной. Так как матрица коэффициентов корреляции симметрична относительно главной диагонали, на которой находятся значения ρ_ij = 1, то формулу (9.7) можно переписать в виде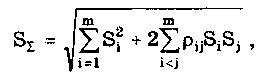



где суммирование во втором слагаемом распространяется на все те составляющие, коэффициенты корреляции которых находятся в матрице правее и выше главной диагонали. Их число равно m(m—1)/2.

Использование последнего уравнения и выражения (9.7) затруднительно, так как точное значение коэффициента корреляции между составляющими обычно неизвестно. В этом случае при расчетах полагают ρ = 0, если случайные составляющие можно считать независимыми (при |ρ| < 0,7), или ρ = ±1, если заметна корреляция между суммируемыми случайными составляющими погрешностей (при |ρ | > 0,7).

При необходимости точного учета коэффициента корреляции между погрешностями аргументов X_i и X_j его оценка может быть найдена по формуле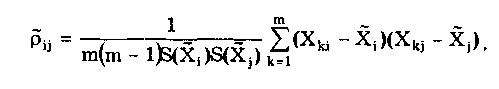

(9.8)

где X_ki, X_kj — элементы выборки аргументов Х_i и Х_j; S(X̃_i), S(X̃_j) — оценки СКО средних арифметических результатов измерений аргументов X_i и Х_j. Оценку коэффициента корреляции можно определить и по формуле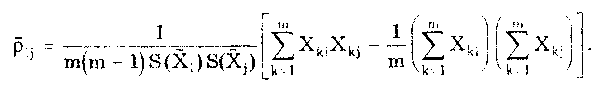

(9.9)

Полезной может оказаться формула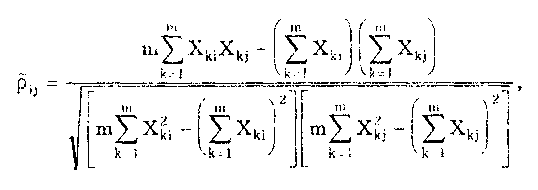

(9.10)

основным достоинством которой является отсутствие необходимости предварительного вычисления СКО составляющих X_kj и X_ki. Следует отметить, что формулы (9.8)—(9.10) равнозначны.

В случае суммирования нормально распределенных случайных погрешностей результирующая погрешность измерения состоит из m случайных составляющих. Зная доверительную вероятность Р и доверительный интервал Д_: для каждой составляющей погрешности, можно найти оценку СКО любой из них по формуле

(9.11)

где z_pj — квантиль нормального распределения, соответствующий доверительной вероятности Р_j. Если значение Р для всех составляющих одинаково, то, используя выражения (9.7) и (9.11), получаем:

а) для коррелированных составляющих (ρ_ij = ±1)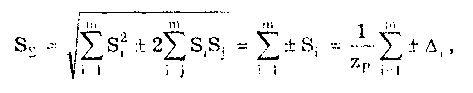

(9.12)

где знак "±" означает, что для составляющих с положительной корреляцией величины S_i и _i нужно брать со знаком "+", а для составляющих с отрицательной корреляцией — со знаком "-"; б) для независимых составляющих (ρ_ij = 0)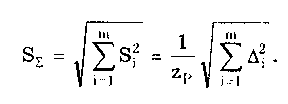

(9.13)

При суммировании составляющих с нормальным законом распределения результирующая погрешность также будет распределена нормально. Поэтому доверительный интервал суммарной погрешности с доверительной вероятностью Р может быть найден как

(9.14)

С учетом (9.12) и (9.13) выражение (9.14) принимает вид, соответственно для коррелированных и некоррелированных составляющих: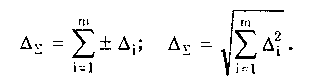

(9.15)

Суммирование погрешностей по первой формуле называется арифметическим, а по второй — геометрическим. Действительные значения коэффициентов корреляции по абсолютному значению могут находиться в пределах от нуля до единицы, поэтому арифметическое суммирование обычно дает завышенное значение суммарной погрешности, а геометрическое — заниженное, т.е. действительное значение находится в интервале между ними.

Закон распределения результирующей погрешности зависит от конкретных видов и характеристик законов распределения суммируемых составляющих. Исходя из этого для определения доверительного интервала суммарной погрешности необходимо в каждом конкретном случае по известным законам суммируемых составляющих установить методами теории вероятностей результирующий закон распределения. Зная его и соответственно квантильный множитель z_p, можно найти доверительный интервал суммарной погрешности по формуле (9.14).

Возможны приближенные способы определения доверительного интервала суммарной погрешности без установления результирующего закона распределения (они рассмотривались в разд. 9.1).

9.4. Суммирование систематических и

случайных погрешностей

При проведении многократных измерений случайная погрешность может быть уменьшена во много раз. Однако погрешность усредненного результата будет определяться не этой весьма малой случайной погрешностью, а не зависящей от числа усредняющих отсчетов систематической погрешностью.

Механизм суммирования систематической и случайной составляющих погрешности отличается от механизма суммирования случайных погрешностей. Согласно ГОСТ 8.207—76 погрешность результата измерения определяется по следующим правилам. Если границы неисключенной систематической погрешности 6 и оценка СКО результата измерения S связаны соотношением

(9.16)

то следует пренебречь систематической составляющей погрешности и учитывать только случайную погрешность результата. При этом доверительные границы погрешности результата  = t_pS, где t_p — коэффициент Стьюдента, зависящий от доверительной вероятности Р и числа проведенных измерений п. Если же имеет место неравенство

(9.17)

то, наоборот, следует пренебречь случайной составляющей и результат характеризовать лишь границами его суммарной систематической погрешности  = . Погрешность, возникающая из-за пренебрежения одной из составляющих погрешности, при выполнении указанных неравенств не превышает 15%.

Числа 0,8 и 8 в стандарте никак не обосновываются. Однако если принять во внимание, что, как было показано ранее, _0,9 = 1,6S, то условие (9.16) эквивалентно неравенству  < _{0 9}/2. Условие (9.17) эквивалентно неравенству  > 5_0,9. Следовательно, ГОСТ 8.207-76 разрешает пренебрегать систематической составляющей и учитывать только случайную составляющую лишь тогда, когда она в 2 раза превышает систематическую. Если же случайная составляющая менее 1/5 систематической, ею можно пренебречь.

При невыполнении неравенств (9.16) и (9.17) границу суммарной погрешности ГОСТ 8.207-76 предписывает находить путем композиции распределений случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины. Допускается границы погрешности результата измерений определять по формуле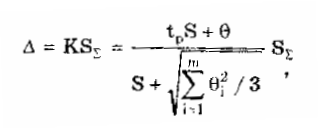



где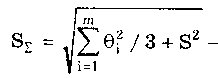- оценка суммарного СКО суммарной погрешности.

Данный подход, приводящий к заниженным оценкам, вызывает [4] справедливые нарекания и вряд ли его следует считать правомочным. Рассмотрим этот вопрос подробнее.

Систематическая погрешность, присутствующая во всех отсчетах, не усредняется при статистической обработке. На рис. 9.1 показаны истинное значение измеряемой величины х_и, границы систематической погрешности , распределение случайной составляющей погрешности р(х). Из рисунка ясен механизм суммирования составляющих погрешности. Если систематическая составляющая постоянна, то ее модуль || должен суммироваться с доверительным интервалом случайной составляющей t_pS, а отнюдь не с СКО. Доверительный интервал суммарной погрешности

Из рис. 9.1 становятся понятными рассмотренные выше условия, при которых можно пренебречь одной из составляющих суммарной погрешности. На рис. 9.1,а показана ситуация, когда нельзя пренебречь ни одной из составляющих. На рис. 9.1,6 доверительный интервал случайной составляющей более чем в два раза больше систематической составляющей, и последней можно пренебречь. На рис. 9.1,в систематическая составляющая превышает доверительный интервал случайной составляющей более чем в 5 раз, и ее также можно не учитывать при определении суммарной погрешности.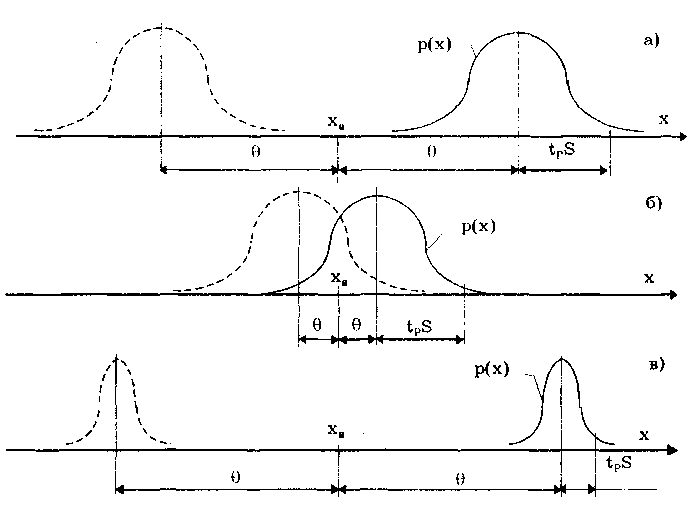



Рис. 9.1. Систематическая и случайная составляющие погрешности

9.5. Критерий ничтожно малой погрешности

Вопрос о том, какими составляющими при расчете погрешностей можно пренебрегать, возникает постоянно. Это связано с тем, что степень точности определения суммируемых погрешностей невысока, поэтому нет смысла суммировать те из них, которые имеют по сравнению с другими малые значения, "поскольку это не повысит точности суммарной погрешности. Пренебрежение малыми погрешностями позволит упростить вычисления при нахождении результирующей погрешности. Следовательно, необходимо установить критерий ничтожно малой погрешности, т.е. математическое правило, позволяющее исключать последнюю из расчета. Этот критерий также необходим при выборе класса точности образцового средства измерений в зависимости от класса точности поверяемого средства измерений.

Один из возможных вариантов определения критерия ничтожно малой погрешности состоит в том, что если одна величина больше другой на порядок, то ею можно пренебречь.

При сложении некоррелированных случайных составляющих суммируются их дисперсии (СКО). В случае двух составляющих суммарная случайная погрешность определяется по формуле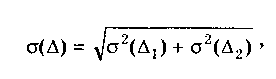



где (₁), (₂) — СКО первой и второй составляющих.

В соответствии с критерием, если дисперсия первой составляющей ²(₁), больше дисперсии второй составляющей ²(₂), более чем в 10 раз, то СКО (), суммарной случайной погрешности составит 1,05(₁). Следовательно, пренебрежение дисперсией второй составляющей по сравнению с дисперсией первой составляющей приводит к тому, что СКО суммарной случайной погрешности будет определено с ошибкой в 5%. Критерий ничтожно малой погрешности для СКО случайной погрешности запишется в виде (₁) > 10̅(₂)  3(₂). Таким образом, погрешностью можно пренебречь, если ее СКО или доверительный интервал в 3 раза меньше, чем у оставляемых погрешностей.

Известен и другой подход к определению критерия ничтожной малости составляющих погрешности, рассмотренный в разд. 9.4.

Для погрешности средств измерений [58] предложен иной критерий существенности ее составляющих.
Пример 9.2. Цифровым измерителем иммитанса Е7-14 проводились прямые многократные измерения сопротивления магазина сопротивлений марки РЗЗ, номинальное значение которого равно 0,1 Ом. Измерения проводились в диапазоне рабочих температур измерителя иммитанса. Получены следующие результаты измерения R_i: 145,44; 145,36; 145,43; 145,38; 145,44; 145,42; 145,41; 145,39; 145,40; 145,41; 145,45; 145,43; 145,46; 145,37; 145,48 мОм. Проведенные измерения характеризуются неисключенной систематической погрешностью, задаваемой пределом допускаемого значения:

• основной погрешности измерения измерителя Е7-14. Формулы для расчета этого значения приведены в таблице примера 9.1. При этом для данного магазина сопротивлений добротность Q = 0;

• дополнительной погрешности измерения в диапазоне рабочих температур. Он равен удвоенному допускаемому значению основной погрешности.

Для устранения влияния соединительных проводов и переходных сопротивлении контактов был проведен ряд измерений при нулевом значении магазина сопротивлений. Получены следующие результаты измерения R_oi: 48,30; 48,29; 48,28; 48,29; 48,28; 48,29; 48,29; 48,28; 48,30; 48,30; 48,30; 48,30; 48,31; 48,32; 48,30 мОм.

Требуется провести обработку результатов измерений. Найти суммарную погрешность измерения сопротивлений.

Суммарная погрешность измерения сопротивления складывается из случайной и систематической погрешностей. Систематическая погрешность измерения сопротивления состоит из трех составляющих, обусловленных:

• ненулевым значением сопротивления соединительных проводов и переходных контактов зажимов используемых средств измерений;

• основной и дополнительной погрешностями измерителя иммитанса Е7-

Первая из них может быть оценена исходя из данных измерений нулевого сопротивления магазина. Полученный ряд данных характеризуется средним арифметическим значением и оценкой его СКО: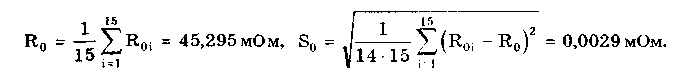



Сопротивление проводов постоянно присутствует в результатах измерений и по своей сути является систематической погрешностью, которая может быть исключена из результатов измерений путем введения поправки, равной -42,295 мОм.

Доверительный интервал погрешности измерения сопротивления проводов, равный _0,95(R₀) = t_pS_o = 2,150,0029 = 0,0062 мОм, можно рассматривать двояко: как неисключенную систематическую погрешность и как составляющую случайной погрешности. В любом случае, как это будет видно далее, ее значение столь мало, что согласно критерию ничтожно малой погрешности ею можно пренебречь.

После введения поправки получается исправленный ряд значений сопротивления R_Иi: 100,145; 100,065; 100,135; 100,085; 10ff,145; 100,125; 100,115; 100,095; 100,105; 100,115; 100,155; 100,135; 100,165; 100,075; 100,185 мОм.

Составляющая систематической погрешности, обусловленная основной погрешностью измерителя иммитанса Е7-14, рассчитывается по формуле

Здесь R̅_n — среднее арифметическое значений ряда неисправленных показаний измерителя иммитанса, равное 145,418 мОм. Следовательно, систематическая погрешность, обусловленная основной погрешностью Е7-14



Систематическая погрешность, обусловленная дополнительной погрешностью средства измерений,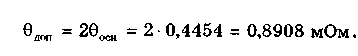



Суммарная систематическая погрешность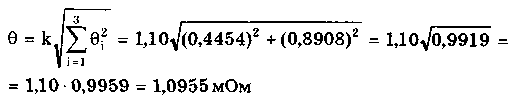



при условии, что коэффициент k в используемой для расчетов формуле (9.6) определяется из табл. 9.1 для Р = 0,95.

Характеристики случайной составляющей находятся посредством статистической обработки исправленного ряда наблюдений. Среднее арифметическое значение сопротивления и его СКО, соответственно равны: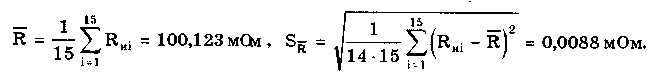



Считая распределение результатов измерений R. нормальным, по таблице из приложения 1 находим коэффициент Стьюдента для числа измерений n =15 и 0,95. Он равен t_p =2,15. В этом случае доверительная граница случайной составляющей погрешности измерений

_0,95(R̅) = t_pS_R̅ = 2,150,0088 = 0,0189мОм.
Случайные погрешности измерений исследуемого сопротивления и сопротивления подводящих проводов можно считать некоррелированными, так как измерения проводились в разное время. Поэтому суммарная случайная погрешность определится в соответствии со вторым уравнением в (9.15):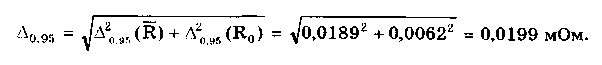



Из полученных данных видно, что систематическая погрешность значительно больше случайной, поэтому, согласно ГОСТ 8.207-76, последнюю можно не учитывать. Результат измерения запишется в виде R=100,l ± l,l мОм при Р = 0,95.
Контрольные вопросы
1. На чем основана теория расчетного суммирования погрешностей?

2. Как могут быть определены квантильные множители суммарной погрешности результата измерения?

3. Сформулируйте правила, по которым суммируются систематические погрешности.

4. Расшифруйте понятия коррелированных и некоррелированных случайных величин. Что считается границей между этими случайными величинами при их суммировании?

5. Каким образом суммируются коррелированные случайные величины?

6. По каким правилам суммируются некоррелированные случайные величины?

7. Как суммируются случайные и систематические погрешности? Какой нормативный документ регламентирует эти правила?

8. В чем состоит суть критерия ничтожно малой погрешности?