Сергеев - Метрология. В. Г. Фирстов Кандидат физикоматематических наук
 Скачать 4.38 Mb. Скачать 4.38 Mb.
|
10.1.2. Классификация помехИзмерительные сигналы редко присутствуют в средствах измерений в чистом виде. Практически всегда на них накладываются помехи. Под помехой понимается сигнал, однородный с измерительным и действующий одновременно с ним. Его присутствие приводит к появлению погрешности измерения. Классификация помех возможна по ряду признаков. По месту возникновения помехи делятся на внешние и внутренние. Причиной возникновения внешних помех являются природные процессы и работа различных технических устройств. Последние создают так называемые индустриальные помехи. Внутренние помехи обусловлены процессами, происходящими при работе самого средства измерений. В зависимости от вида включения источников помехи и измерительного сигнала в эквивалентных схемах средств измерений различают помехи общего вида (синфазные) и помехи нормального (последовательные) вида [69, 71]. Источник помехи общего вида включен между общими точками (корпусами) схем объекта измерений и СИ. Источник помехи нормального вида включен последовательно во входную цепь СИ. По виду частотного спектра помехи делятся на белый и розовый шумы. Спектральные составляющие белого шума равномерно распределены по всему частотному диапазону. У розового шума спектральная мощность, приходящаяся на декаду частоты, постоянна. По основным свойствам помехи можно разделить на три вида: флуктуационные, сосредоточенные и импульсные. Флуктуационные помехи представляют собой хаотическое, беспорядочное изменение во времени сигнала, однородного с измеряемым, в каком-либо месте средства измерений. Такие помехи часто называют шумом. Пример — внутренние шумы измерительных электронных усилителей. Различают следующие виды шумов: • тепловой (шум Джонсона), по своим свойствам близкий к белому шуму. Тепловой шум генерируется любым резистором, находящимся в измерительной цепи. Значение его состоит в том, что он устанавливает нижнюю границу напряжения шумов любого измерительного преобразователя, имеющего выходное сопротивление; • дробовый, обусловленный движением электронов — дискретных носителей электрического тока. Он имеет равномерный спектр, т.е. является белым; • фликкер-шум. К данному виду относят шумы, у которых спектральная мощность на декаду частоты примерно постоянна, т.е. розовые шумы, например шум постоянного резистора, пропорциональный протекающему через него току, шум тока базы транзистора и др. Влияние флуктуационной помехи уменьшается при усреднении суммы измерительного сигнала и помехи. Максимальное уменьшение влияния флуктуационной помехи на результат измерения возможно в том случае, когда спектральная плотность помехи постоянна в пределах полосы пропускания средства измерений, т.е. помеха имеет характер белого шума. Сосредоточенными называют помехи, основная часть мощности которых сосредоточена на отдельных участках диапазона частот, меньших полосы пропускания СИ. Помехи, наводимые в измерительных цепях СИ от промышленной силовой сети частотой 50 Гц, являются сосредоточенными. Эффективность их подавления в значительной мере определяется достоверностью априорных данных о частотном спектре. Импульсными помехами называется регулярная или хаотическая последовательность импульсных сигналов, однородных с измерительным сигналом. Источниками таких помех являются цифровые и коммутирующие элементы СИ или работающего рядом с ними устройства. Характерный пример импульсных помех — помехи от устройств зажигания двигателей внутреннего сгорания. Импульсные и сосредоточенные помехи часто называют наводками. Поскольку основным следствием действия помехи является появление погрешности измерения, то стараются устранить или, по крайней мере, ослабить их действие на средства измерений. Для устранения влияния помех целесообразно, если это возможно, исключить причины их возникновения. Способы борьбы с помехами в значительной мере зависят от их спектрального состава, вида измерительного сигнала и помехи. Многие из электрических помех можно устранить путем экранирования, заземления средства измерений, применения специальных фильтров. Тепловые шумы могут быть заметно уменьшены при охлаждении их источника. Однако в целом борьба с помехами чрезвычайно сложна и является скорее искусством, нежели наукой. В отдельных случаях приходится применять особенно изощренные меры, как то: использование монолитных каменных столов для исключения посторонней вибрации, размещение средств измерений или их частей в термостатах, проведение электрической и электромагнитной экранировки помещений для устранения электромагнитных наводок. 10.2. Математическое описание измерительныхсигналовВ метрологии измерительные сигналы описываются математическими моделями вида Y = f(X, А, В, С,...), где Y — основной информативный параметр сигнала; X — независимый аргумент сигнала; А,В,С — параметры сигнала. В зависимости от рода независимого аргумента сигналы описываются временными (X = t) и частотными (X = о)) математическими моделями. Вид модели выбирается в зависимости от конкретных условий решаемой задачи. Во временной области применяют известные математические функции f(t, А, В, С,...), наиболее точно описывающие изменение сигнала, в которых один из параметров А, В, С и т.д. зависит от измеряемой величины. Временная форма представления сигнала позволяет легко определить такие важные характеристики, как энергия, мощность и длительность сигнала. Наряду с временным описанием сигналов широко используется их спектральное (частотное) представление. В процессе передачи и обработки сигналов оно играет особую роль, поскольку определяет параметры используемой аппаратуры. Частотное представление основывается на преобразовании Фурье сигнала Y(t): 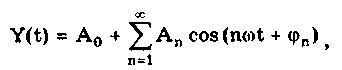 где А0 — постоянная составляющая; Аn, п— амплитуда и фаза n-й гармоники. Множество значений Аn() и n() образуют соответственно амплитудный и фазовый спектры, которые характеризуют свойства сигнала Y(t) в частотной области. Такой спектр называют линейчатым, или дискретным. Различные формы представления спектра периодического сигнала могут быть также найдены с помощью выражений (10.1) — (10.3). Характерный вид амплитудного и фазового спектров для некоего периодического сигнала приведен на рис. 10.3. 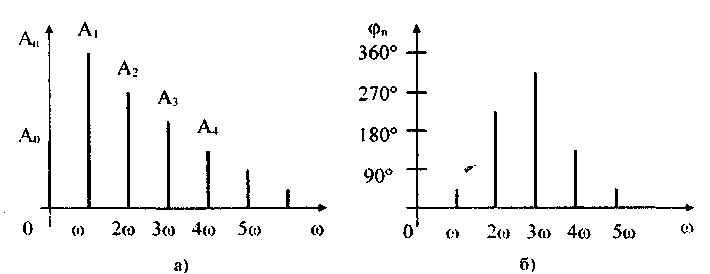 Рис. 10.3. Амплитудный (а) и фазовый (б) дискретные спектры При постепенном увеличении периода сигнала (в пределе до бесконечности) разности соседних частотных составляющих спектра становятся ничтожно малыми и дискретный спектр превращается в непрерывный. Для описания непрерывного спекра непериодического сигнала Y(t) используют спектральную функцию S(), модуль спектральной функции |S()|, часто называемый спектром, и аргумент спектральной функции argS(). Спектральную функцию можно определить с помощью интеграла Фурье: 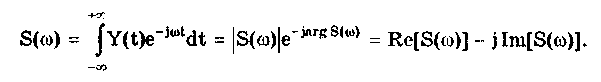 Здесь Re[S()] и Im[S()]— действительная и мнимая части спектральной функции: 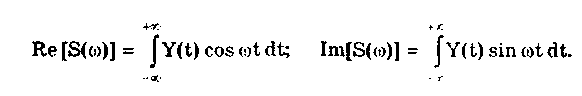 Модуль и аргумент спектральной функции определяются соответственно по формулам: 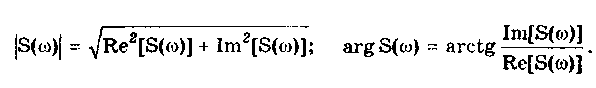 Спектральная функция S() является комплексной величиной, содержащей информацию о спектре и амплитуд, и фаз, поэтому часто ее называют комплексным спектром. Модуль функции S() является спектром амплитуд, но он выражает но непосредственно амплитуду, а ее спектральную плотность. Спектральное представление сигнала позволяет оценить его частотный диапазон, т.е. граничные частоты, между которыми заключены все или основные, имеющие наибольшие амплитуды гармонические составляющие сигнала. Частотный диапазон является важной характеристикой сигнала, определяющей необходимую полосу пропускания средства измерения для передачи сигналов с требуемой точностью. 10.3. Математические модели элементарныхизмерительных сигналовК элементарным измерительным сигналам относятся постоянный во времени сигнал и сигналы, описываемые единичной и синусоидальной функциями, а также дельта-функцией. Постоянный сигнал — самый простой из элементарных сигналов, описываемый математической моделью вида Y = А, где А — единственный параметр сигнала. Графики временной и частотной моделей постоянного сигнала приведены на рис. 10.4. 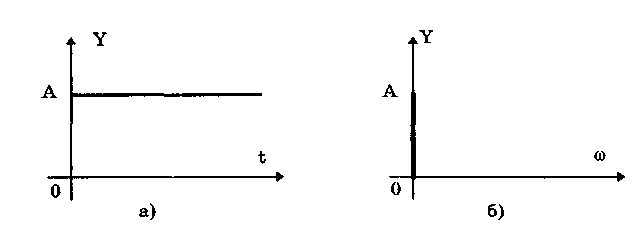 Рис. 10.4. Графики временной (а) и частотной (б) моделей постоянного сигнала Единичная функция, называемая иногда функцией Хевисайда, описывается уравнением 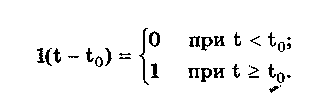 Она имеет один параметр — момент времени t0. Ее временная и частотная модели представлены на рис. 10.5,а. Дельта-функция описывается уравнением 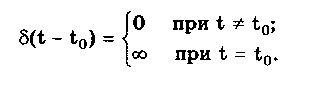 Она также имеет один параметр — момент времени t0. Графики временной и частотной моделей дельта-функции (t) показаны на рис. 10.5, б. Из них видно, что дельта-функция имеет спектр бесконечной ширины. 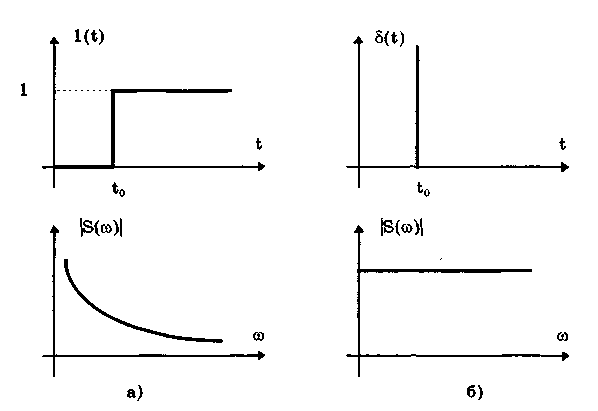 Рис. 10.5. График моделей единичной (а) и дельта-функции(б) Дельта-функция обладает следующим свойством: 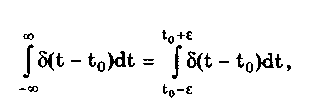 где — любое, сколь угодно малое число. Она может рассматриваться как предельная функция однопараметрического семейства непрерывных функций, например нормального распределения с бесконечно малым СКО : 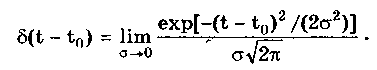 Единичная и дельта-функции связаны между собой следующими выражениями: 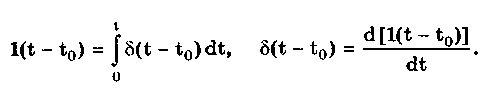 Важной особенностью дельта-функции является стробирующее действие, которое описывается уравнением 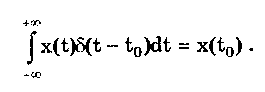 Оно используется для представления дискретизированной во времени функции с шагом дискретизации t: 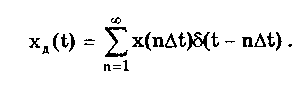 Гармонический сигнал описывается уравнением 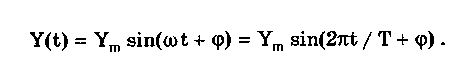 (10.5) (10.5)Параметрами такого сигнала являются: амплитуда Ym, период Т (или частота f=l/T, или круговая частота ) и начальная фаза . График временной модели общеизвестен, а график частотной модели такого сигнала показан на рис. 10.6 . Рис. 10.6. Спектр гармонического сигнала 10.4. Математические модели сложныхизмерительных сигналовВ средствах измерений используется большое число измерительных сигналов, имеющих самые разнообразные формы. Рассмотрим некоторые из них, наиболее часто встречающиеся на практике. Прямоугольные импульсы. Одиночный идеальный прямоугольный импульс (рис. 10.7,а) описывается уравнением 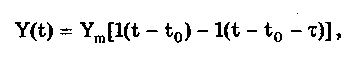 т.е. он формируется как разность двух единичных функций, сдвинутых во времени на величину т — длительность импульса. 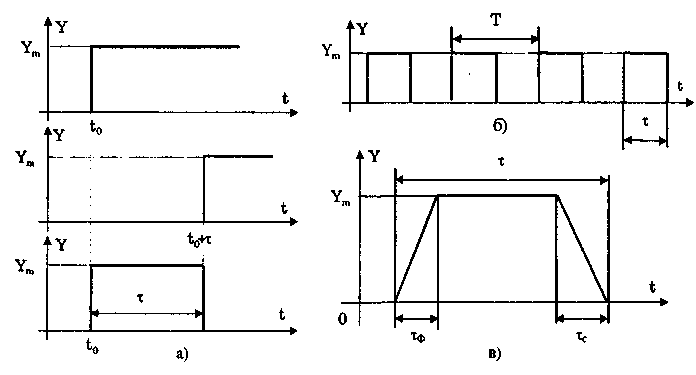 Рис. 10.7. Формирование идеального прямоугольного импульса (а), последовательность прямоугольных импульсов (б) и трапецеидальный импульс (в) Последовательность прямоугольных импульсов есть сумма одиночных импульсов: 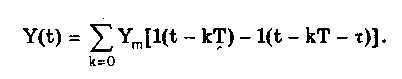 Для ее описания необходимо знать три параметра: амплитуду Ym, длительность Т и период Т (рис. 10.7, б). Отношение периода к длительности прямоугольного импульса называется скважностью, а обратная величина — коэффициентом заполнения. При скважности, равной двум, последовательность импульсов называют меандром (см. рис. 10.7, б). Идеальные прямоугольные импульсы в природе не встречаются. В реальных импульсах время изменения сигнала от нулевых до амплитудных значений (и обратно) всегда имеет конечную длительность, т.е. фронт Тф и спад Тс (рис. 10.7, в). Следовательно, у реальных импульсов будет трапецеидальная форма. Трапецеидальный импульс также является идеализации реальных импульсов, которые имеют гораздо более сложную форму. Она отличается от трапеции спадом вершины импульса, выбросами на вершине и в паузе и другими особенностями, учтенными в системе параметров реального прямоугольного импульса по ГОСТ 16465-70. Сигналы с линейными участками. При построении средств измерительной техники широкое применение находят периодические сигналы с линейными участками. Это прежде всего линейный знакопеременный и однополярный линейно изменяющийся (пилообразный) сигналы (рис. 10.8). Линейный знакопеременный сигнал описывается уравнением 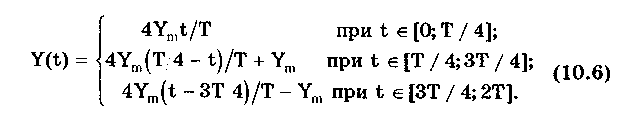 Пилообразный сигнал 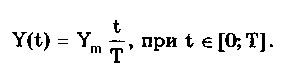 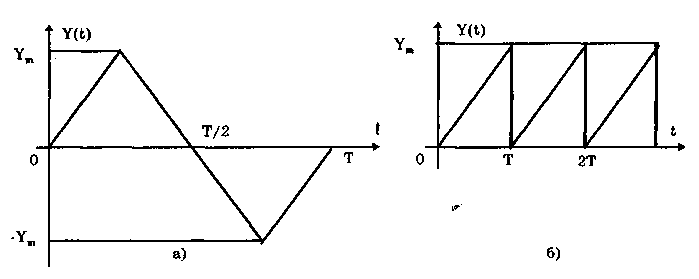 Рис. 10.8. Линейный знакопеременный (а) и однополярный линейно изменяющийся (пилообразный) (б) сигналы Пример 10.1. Оценить нижнюю и верхнюю частоты полосы пропускания измерительного канала средства измерений, используемого для определения параметров трех сигналов одинаковой частоты <й и амплитуды Ym=A: Yj(t) — синусоидального, описываемого формулой (10.5) при = 0; Y2(t) — линейного знакопеременного, описываемого формулой (10.6); Y3(t) — знакопеременного меандра, описываемого формулой  Чтобы средство измерений позволяло точно определять параметры сигнала, оно не должно искажать его форму в процессе преобразований. Для этого все гармоники сигнала должны проходить через измерительный канал без искажений. Выполнение данного условия нереально, так как полоса пропускания СИ конечна, а число гармоник в спектре бесконечно. Поэтому в качестве критерия выбора максимальной частоты полосы пропускания измерительного канала примем следующее условие: для внесения минимальных искажений в форму измеряемого сигнала канал должен пропускать без искажений его гармоники, амплитуда которых превышает, например, 1% амплитуды первой гармоники. Это не очень строгая постановка вопроса, однако она позволит решить поставленную задачу. Определим спектральный состав измеряемых сигналов, разложив их в ряд Фурье: 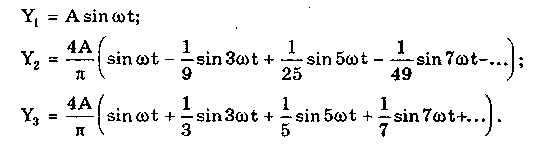 Спектр первого сигнала содержит только первую гармонику с амплитудой А. Спектры второго и третьего сигналов содержат только нечетные гармоники, амплитуда которых затухает с разной интенсивностью: у сигнала Y2 — пропорционально 1/n2, где n — номер гармоники, а у сигнала Y2 — пропорционально 1/n. Соответственно номер гармоники второго сигнала, после которой их амплитуда становится меньше 0,01A1, равен 11 (100/112=0,83%). Для третьего сигнала это номер 101 (100/101=0,99%). Таким образом, при измерении синусоидального сигнала минимальная и максимальная частоты полосы пропускания канала одинаковы и равны со. При измерении линейного знакопеременного сигнала они соответственно составят и 11. Полоса пропускания равна 10. Для знакопеременного меандра экстремальные частоты равны и 101, а полоса пропускания — 100. Модулированные сигналы. Модулированным называется сигнал, являющийся результатом взаимодействия двух или более сигналов, т.е. модуляции. Модуляция — это воздействие измерительного сигнала X(t) на какой-либо параметр стационарного сигнала Y(t), обладающего такими физической природой и характером изменения во времени, при которых удобны его дальнейшие преобразования и передача. В качестве стационарного сигнала, именуемого несущим, обычно выбирают синусоидальное (гармоническое) колебание (10.7) или последовательность импульсов. Физический процесс, обратный модуляции, называется демодуляцией, или детектированием, и заключается в получении из модулированного сигнала другого сигнала, пропорционального модулирующему. Задача демодуляции — по возможности полное восстановление информации, содержащейся в модулирующем сигнале X(t). Вид модуляции и способ детектирования зависят от требований, предъявляемых к точности передачи информации. Наиболее простым модулированным гармоническим сигналом является ам-плитудно-модулированный сигнал, в котором измерительная информация содержится в амплитуде несущего синусоидального сигнала (рис. 10.9). 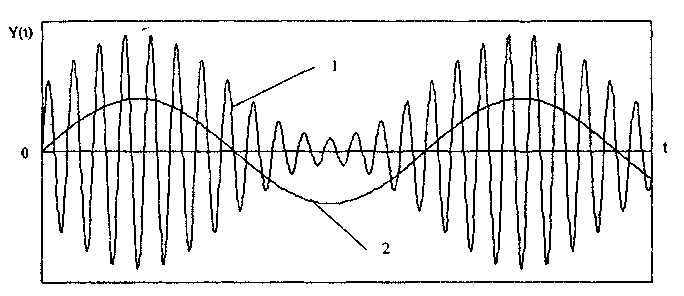 Рис. 10.9. Амплитудно-модулированный (1) и модулирующий (2) сигналы Амплитудно-модулированные сигналы описываются формулой 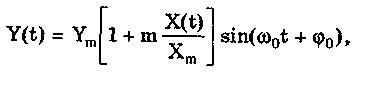 (10.8) (10.8)где m — глубина амплитудной модуляции (всегда меньше единицы). При частотной модуляции (рис. 10.10) измерительная информация содержится в частоте модулированного сигнала, т.е. 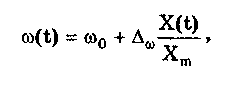 где — наибольшее изменение частоты модулированного сигнала, т.е. девиация частоты, пропорциональная амплитуде модулирующего сигнала. При фазовой модуляции (рис. 10.11) модулирующий сигнал X(t) воздействует на фазу несущего колебания: 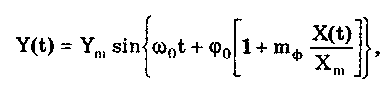 где mф — коэффициент фазовой модуляции. 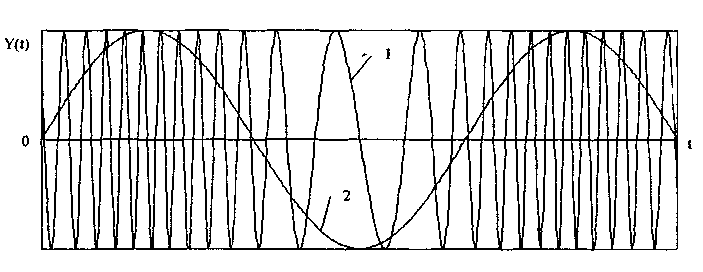 Рис. 10.10. Частотно-модулированный (1) и модулирующий (2) сигналы Для того чтобы при детектировании можно было восстановить модулирующий сигнал, необходимо иметь сигнал вида (10.7), называемый опорным. Относительно него наблюдают, как меняется фаза модулированного сигнала. Модулирующий, модулированный и опорный сигналы показаны на рис. 10.11. 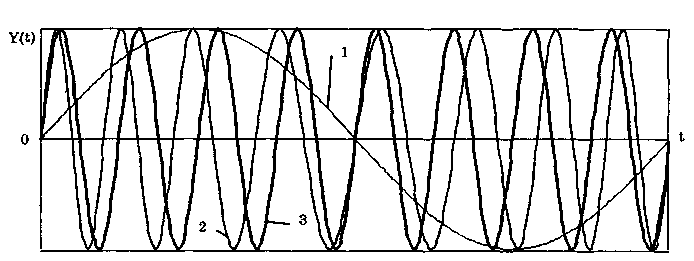 Рис. 10.11. Модулирующий (1), фазомодулированный (2) и опорный (3) сигналы Если модулируемым сигналом является периодическая последовательность прямоугольных импульсов, уо возможны три вида модуляции (рис. 10.12): • амплитудно-импульсная (АИМ); • частотно-импульсная (ЧИМ); • широтно-импульсная (ШИМ). 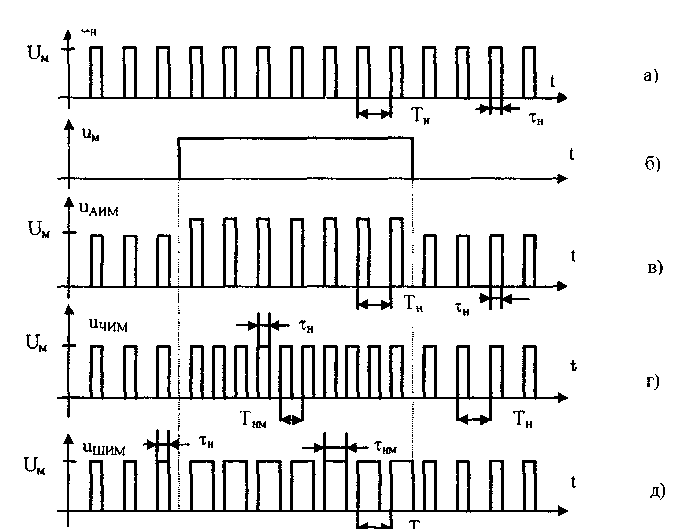 Рис. 10.12. Несущая последовательность прямоугольных импульсов (а), модулирующий (б), амплитудно-модулированный (в), частотно-модулированный (г) и широтно-модулированный (д) сигналы При этом параметром, несущим измерительную информацию, соответственно являются амплитуда, частота и длительность импульсов. 10.5. Квантование и дискретизацияизмерительных сигналовПо характеру изменения информативного параметра сигналы делятся на четыре группы: • непрерывный по времени и размеру; • непрерывный по времени и квантованный по размеру; • дискретизированный по времени и непрерывный по размеру; • дискретизированный по времени и квантованный по размеру. Сигналы, непрерывные по времени и размеру, — наиболее распространенные (см. рис. 10.2,а и кривая 1 на рис. 10.13). Они чаще всего встречаются в практике измерений, поскольку все первичные природные сигналы макромира непрерывны по времени и размеру. Такие сигналы определены в любой момент времени существования сигнала и могут принимать любые значения в диапазоне его изменения. 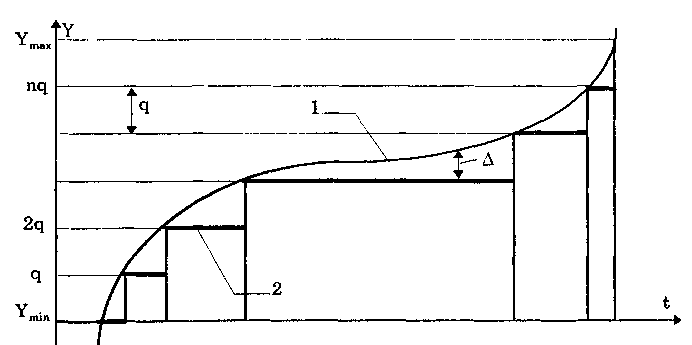 I Рис. 10.13. Исходный непрерывный (1) и непрерывный по времени и квантованный по размеру (2) сигналы Сигналы, непрерывные по времени и квантованные по размеру получаются из сигнала, непрерывного по времени и размеру, посредством его квантования. Квантование — измерительное преобразование непрерывно изменяющейся величины в ступенчато изменяющуюся с заданным размером ступени q — квантом. В результате проведения этой операции непрерывное множество значений сигнала Y(t) в диапазоне от Ymin до Ymax преобразуется в дискретное множество значений YKB(t) (см. рис, 10.13). Квантование широко применяется в измерительной технике. Существует большая группа естественно квантованных физических величин. К ним относятся электрический заряд, квантом которого является заряд электрона, масса тела, квантом которой является масса молекулы или атома, составляющих данное тело, и др. Различают равномерное (q — постоянная величина) и неравномерное (q — переменная величина) квантование. Неравномерное квантование применяется достаточно редко, в специфических случаях, например при большом динамическом диапазоне квантуемой величины. В связи с этим в дальнейшем рассматривается только равномерное квантование. Процесс квантования описывается уравнением где Yкв(t) — квантованный сигнал; N(ti) — число квантов; l(t - ti) — единичная функция. Любой процесс измерения по сути своей есть процесс квантования. Например, при измерении длины тела линейкой с миллиметровыми делениями определяется целое число миллиметров, наиболее близкое к истинному размеру тела. В данном случае в роли кванта выступает миллиметр. При использовании микрометра квантом является величина, равная 10-6 м. Разность между истинным значением длины тела и измеренным линейкой есть погрешность квантования. Погрешность квантования — методическая погрешность отражения непрерывной величины ограниченным по числу разрядов числом. Она равна разности между значением непрерывной функции и значением, полученным в результате квантования (см. рис. 10.13). Возможны [13] четыре способа квантования, при которых значение непрерывной аналоговой функции Y(t), находящееся между двумя известными значениями Yi и Yi+1 , где Yi+1= Yi + q, отражается цифровым значением N, полученным после ее квантования. Способы и формулы для расчета числовых значений N и погрешностей квантования приведены в табл. 10.1. Там же приведены максимальные значения погрешности квантования m (Int(x), Frac(x) — целая и дробная части числа х; sign(x) — функция, равная 1 при х > 0 и -1 при х < 0). Таблица 10.1 Способы Квантования
Можно показать [13, 14, 88], что погрешность квантования во всех рассмотренных случаях подчиняется равномерному закону распределения. В первом случае она распределена в диапазоне от 0 до -q и имеет математическое ожидание М[] = -q/2, во втором — от О до + q с М[] = q/2, в третьем и четвертом — от -q/2до + q/2 с М[] = 0. Среднее квадратическое отклонение погрешности при всех видах равномерного квантования () = q/(23̅). Если задано максимально допустимое значение СКО m, то данная формула дает возможность определить число ступеней Nm, при котором СКО погрешности квантования не превысит m. Действительно, учитывая, что q = Xm/Nm, где Xm — максимальное значение квантуемого сигнала, получим исходное неравенство После преобразования 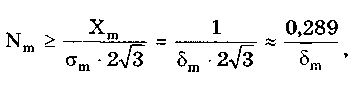 где Cигналы, дискретизированные по времени и непрерывные по размеру получаются из непрерывных по времени и размеру сигналов посредством дискретизации. Дискретизация — измерительное преобразование непрерывного во времени сигнала Y(t) в последовательность мгновенных значений этого сигнала Yk=Y(kt), соответствующих моментам времени kt, где k =1; 2; ... Интервал времени t называется шагом дискретизации, а обратная ему величина f =l/t — частотой дискретизации. Процесс дискретизации непрерывного сигнала показан на рис. 10.14. Математически он описывается с помощью дельта-функции 5(t-kAt), которая, как известно, обладает стробирующим действием. Идеальный дискретизированный сигнал Yfl является последовательностью импульсов нулевой длительности и аналитически может быть представлен в виде 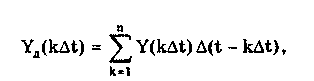 где Y(kt) — значение непрерывного сигнала в k-й точке дискретизации. 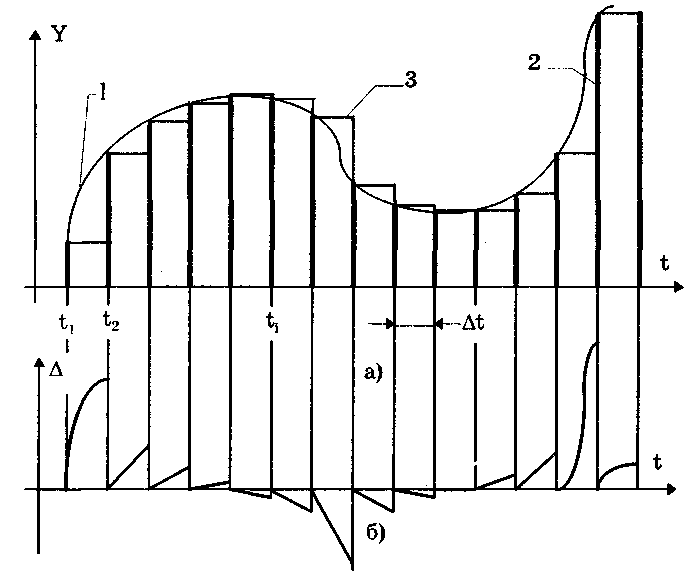 Рис. 10.14. Дискретизация непрерывного сигнала (а) и погрешность восстановления (б): 1 — исходный непрерывный сигнал; 2 — сигнал, дискретизированный-по времени и непрерывный по размеру; 3 — восстановленный с помощью полинома Лагрзнжа нулевой степени непрерывный во времени сигнал Дискретизация бывает равномерной (At = const) и неравномерной (At — переменная величина). Частота дискретизации выбирается на основе априорных сведений о характеристиках дискретизируемого сигнала. На практике наибольшее распространение получила равномерная дискретизация. Это объясняется тем, что алгоритмы дискретизации и последующего восстановления сигнала и соответствующая аппаратура относительно просты. Однако при недостаточности априорных данных о характеристиках сигнала или их некорректности возможна значительная избыточность отсчетов. По способу получения дискретных значений различают физичс скую и аналитическую дискретизации. При физической дискретизации, т.е. дискретизации, осуществляемой аппаратными средствами электроники (рис. 10.15, а), преобразование непрерывного сигнала в последовательность мгновенных значений осуществляется с помощью стробирующего импульса конечной (ненулевой) длительности тс (рис. 10.15, б). Поэтому амплитуда дискретизированных значений может находиться в диапазоне от YBbIX(ti) до YBbIX(ti - c). Поскольку дискретизированное значение относят, как правило, к моменту времени ti,то возникает погрешность датирования отсчета д =YBbIX(ti) — Ycp, максимальное значение которой дm = Yвых(ti + c) - Yвых(ti), где Ycp — некоторое значение сигнала Ycp [Yвыx(ti);Yвых(ti+c)], зависящее от аппаратной реализации устройств, дискретизирующих измерительный сигнал. 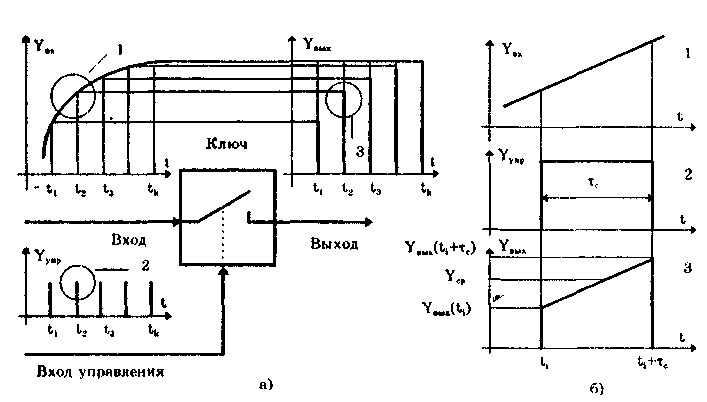 Рис 10.15. Структурная схема процесса физической дискретизации (а) и основные сигналы в укрупненном временном масштабе (б) Дискретизация имеет место в расчетах процессов, проводимых с помощью вычислительной техники. В этом случае она называется аналитической (математической, расчетной, условной). При такой дискретизации длительность стробирующего импульса равна нулю; следовательно, погрешность датирования принципиально отсутствует и дискретизированное значение относится к заданному моменту времени, т.е. определяется мгновенное значение сигнала. В дискретизированном сигнале отсутствуют промежуточные значения, которые содержались в исходном непрерывном сигнале. Однако часто принципиально необходим непрерывный сигнал. Поэтому во многих случаях дискретизированный сигнал требуется преобразовать в непрерывный, т.е. восстановить его промежуточные значения. Задача восстановления дискретизированных сигналов в общем случае аналогична задаче интерполирования функций. При восстановлении исходного сигнала Y(t) по совокупности выборок Yд(kt) формируется обобщенный многочлен где Ci(t) — система базисных функций, которая обычно является ортогональной или ортонормированной; ai — коэффициенты ряда. Его значения в точках дискретизации совпадают со значениями непрерывной функции. В ряде случаев при формировании восстанавливающего многочлена накладывается условие совпадения производных до заданного порядка п включительно. При восстановлении непрерывный сигнал на каждом из участков между соседними дискретными значениями заменяется кривой, вид которой определяется выбранными базисными функциями. Восстановление непрерывного сигнала из дискретизированного должно проводиться с возможно меньшей заданной погрешностью. Для этого необходимо соответствующим образом выбрать для данного участка сигнала восстанавливающую базисную функцию. Коэффициенты ряда и базисные функции могут выбираться на основе различных критериев [14, 88], например: наибольшего отклонения [14], минимума погрешности или совпадения значений восстанавливаемого непрерывного сигнала с мгновенными значениями дискретизированного сигнала. В "измерительной технике наиболее широко используется последний критерий, так как он удобен для аналитического восстановления с помощью компьютера на основе результатов измерения мгновенных значений дискретизированного сигнала, отличается простотой реализации и достаточно высокой точностью. Восстановление сигнала в данном случае регулируется теоремой Котелъникова, которая формулируется следующим образом: если функция Y(t), удовлетворяющая условиям Дирихле — ограничена, кусочно-непрерывна, имеет конечное число экстремумов — и обладающая спектром с граничной частотой fc, дискретизирована циклически с периодом t, меньшим или равным l/(2fc), т.е. fд > 2fc, то она может быть восстановлена по всей этой совокупности ее мгновенных значений без погрешности. Если теорема Котельникова выполняется, то непрерывный сигнал Y(t) может быть восстановлен как сумма базисных функций, называемых рядом Котельникова: 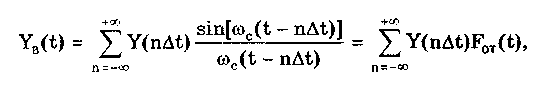 где c=2fc — круговая граничная частота спектра непрерывного сигнала Y(t); t — период дискретизации; Fот(t) — функция отсчетов. Ряд Котельникова является одним из примеров обобщенного ряда Фурье и замечателен тем, что его коэффициенты равны мгновенным дискретизированным значениям сигнала Y(t) и, следовательно, определяются наиболее простым способом. При использовании теоремы Котельникова возникает ряд принципиальных затруднений [13]. Теорема предназначена для сигналов с ограниченным частотным спектром, а реальные сигналы имеют бесконечный частотный спектр. Искусственное ограничение реального бесконечного спектра частотой fc (впредположении, что при частотах, больших fc, спектр равен нулю) приводит к возникновению погрешности восстановления. В действительности дискретизированные значения сигнала практически никогда не являются мгновенными. Чаще всего они выражают усредненное за некоторый конечный (хотя и весьма малый) интервал значение сигнала (см. рис. 10.15,6). Это обуславливает возникновение методической погрешности восстановления сигнала. Кроме полиномов Котельникова широкое применение в качестве базисных функций нашли степенные алгебраические полиномы Лагранжа (см. рис.10.14,6) и Уолша [14]. Погрешность восстановления дискретизированных сигналов равна разности между значениями непрерывной исходной функции и восстанавливающей функции. Она существенным образом зависит от вида используемой базисной функции. Для восстанавливающей функции на основе полиномов Лагранжа нулевой степени погрешность восстановления показана на рис. 10.14, б. Погрешность восстановления зависит от закона изменения дис-кретизируемой функции, выбранных восстанавливающих полиномов и величины шага или частоты дискретизации. Чем менее гладкой и монотонной является дискретизируемая функция (т.е. чем больше в ее спектральном составе высших гармоник), тем больше, при прочих равных, погрешность восстановления. Выбор восстанавливающих полиномов влияет не только на погрешность, но и на сложность и стоимость реализующей данный способ восстановления аппаратуры. Поэтому на практике стремятся использовать по возможности наиболее простые аппроксимирующие выражения. Погрешность восстановления доводят до требуемой величины главным образом соответствующим выбором шага дискретизации. Очевидно, что при его уменьшении погрешность восстановления снижается. Однако при малых t измерительный прибор должен иметь очень высокое быстродействие, что требует усложнения его конструкции и приводит к увеличению стоимости. Кроме этого возникает избыточность информации, приводящая к перегрузке используемых каналов связи и запоминающих устройств. При больших t невозможно точно восстановить исходную непрерывную функцию, поэтому на практике шаг t и частоту дискретизации f=l/t рассчитывают по заданной погрешности восстановления. Методика расчета зависит от применяемых базисных функций. При использовании ряда Котельникова частота дискретизации рассчитывается по формуле f=2kfc, где k — коэффициент запаса, выбираемый [14] из диапазона (1,5; 6) и учитывающий неограниченность спектра реальных сигналов; fc — максимальная частота в спектре сигнала. Формулы для расчета частоты дискретизации при использовании полиномов Лагранжа нулевой и первой степеней носят приближенный характер и подробно рассмотрены в [13]. Сигналы, дискретизированные по времени и квантованные по размеру (рис. 10.16), согласно приведенной классификации являются цифровым сигналами. На практике они формируются цифроаналоговыми преобразователями. Последние фактически являются управляемыми цифровым кодом мерами, выходной сигнал которых подвергнут дискретизации. Следовательно, в этих устройствах параллельно осуществляются два процесса преобразования измерительной информации: дискретизация и квантование. Их совместное действие описывается математическим выражением 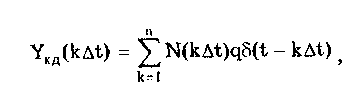 где N(kt) — цифровой код (число квантов), соответствующий моменту kt. 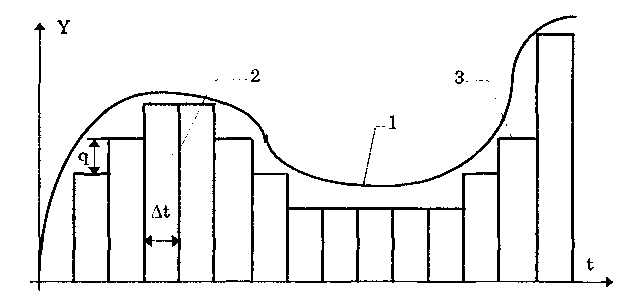 Рис. 10.16. Сигналы: исходный непрерывный (1), дискретизированный по времени и квантованный по уровню (2) и восстановленный непрерывный (3) Значения сигнала, дискретизированного по времени и квантованного по уровню, определены только в моменты, кратные периоду дискретизации At. Поэтому имеет место задача формирования непрерывного сигнала по данным значениям. Эта задача аналогична рассмотренной задаче восстановления дискретизированного сигнала. Отличие состоит в том, что последний равен исходному непрерывному сигналу, а квантованный и дискретизированный сигналы отличаются от него, но не более чем на величину кванта q. Вследствие этого погрешность состоит из двух составляющих, обусловленных процессами дискретизации и квантования. Суммарная дисперсия ординаты восстановленного сигнала равна сумме дисперсий погрешности квантования и дискретизации: 2 = q2/12 + 2д. При этом считается, что между ними отсутствует корреляция. 10.6. Интегральные параметры периодическогосигналаПеременный периодический сигнал Y(t) кроме совокупности мгновенных значений часто описывается несколькими общепринятыми обобщающими параметрами, называемыми интегральными и характеризующими в целом период сигнала. Каждому закону изменения сигнала соответствуют определенные интегральные значения: амплитудное, среднее, средневыпрямленное и среднеквадратическое. Амплитудное (пиковое) значение Ym равно максимальному на периоде значению сигнала Y(t). По сути своей амплитудное значение является мгновенным, а не интегральным. Однако оно используется при расчете коэффициентов формы, амплитуды и усреднения и поэтому рассматривается в этом разделе. Среднее значение описывает постоянную составляющую сигнала. Так, для синусоидального сигнала среднее значение равно нулю, следовательно, он не содержит постоянной составляющей. Средневыпрямленное значение Среднеквадратическое значение 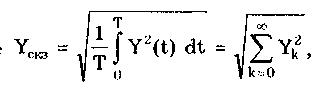 где Yk — среднеквадратическое значение k-й гармоники сигнала Y(t). Его иногда называют действующим или эффективным, хотя эти термины ГОСТ 16465-70 считает устаревшими. Среднеквадратическое значение сигнала является единственной истинной мерой его мощности. Эти значения широко используются в практике электрических измерений. Подавляющее большинство вольтметров програ-дуировано в среднеквадратических значениях напряжения. Связь между перечисленными параметрами устанавливается с помощью следующих коэффициентов: формы kф = Yскз/Yсвз, амплитуды ka = Ym/Yскз и усреднения ky = Ym/Yсвз = kakф. Числовые значения рассмотренных коэффициентов для некоторых сигналов приведены в табл. 10.2. Таблица 10.2 Значения коэффициентов амплитуды, формы в усреднения для ряда наиболее распространенных сигналов
Пример 10.2. В измерительной технике часто используются периодические и не содержащие постоянной составляющей сигналы. Они имеют самую разнообразную форму: прямоугольную, линейную знакопеременную, синусоидальную и т.д. до близкой к форме дельта-функции Дирака. Для моделирования и настройки средств измерений удобно иметь одну простую математическую функцию, которая при изменении одного—двух ее параметров описывала бы с той или иной степенью точности все перечисленные выше формы сигналов. Для данной цели подходит известная функция Иордана 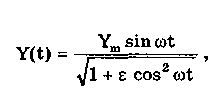 (10.9) (10.9)где Ym— амплитуда сигнала; = 2f— круговая частота; — параметр формы, изменяющийся от -0,(999) до бесконечности. При - 1, получаем практически прямоугольный сигнал, а при данная функция по форме становится близкой к дельта-функции Дирака (рис. 10.17). 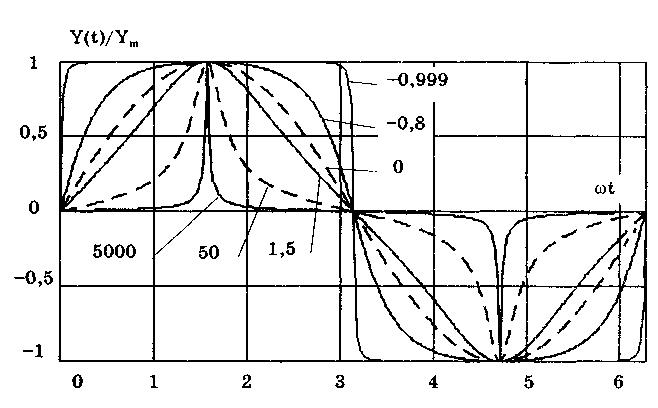 Рис. 10.17. Вид функции Иордана при различных значениях коэффициента Среднеквадратическое и средневыпрямленное значения сигнала, описываемого функцией Иордана, зависят от параметра формы и могут быть определены по формулам: 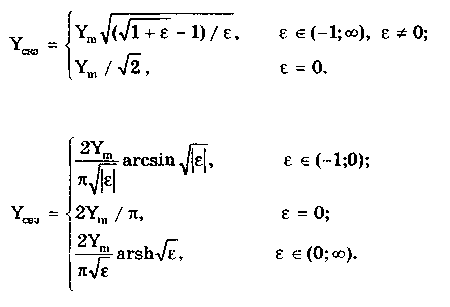 Приведенные выражения позволяют найти все три коэффициента, характеризующие сигнал (10.9). Эти коэффициенты, а также коэффициент гармоник kг, рассчитываемый по формуле (10.4), в значительной степени зависят от параметра формы . Рассчитанные зависимости приведены в табл. 10.3. Таблица 10.3 Значения коэффициентов kф(), ka() и kr() функции Иордана при различных значениях
Анализ приведенных данных показывает, что формула (10.9) описывает сигналы, формы которых близки к прямоугольной ( > -0,(999)), линейной знакопеременной ( 1,5 ... 2), синусоидальной ( = 0) и дельта-функции Дирака ( > 5000). Изменяя один параметр функции, можно описывать сигнал различным спектральным составом: коэффициент гармоник меняется от 0 при = 0 до 173% при = 5000. Функцию Дирака удобно использовать при реализации калибраторов — прецизионных источников переменного напряжения, выполненных на основе цифроаналоговых преобразователей, управляемых микропроцессорами. Задавая параметр формы и рассчитывая управляющий код для данного преобразователя, можно формировать напряжения требуемой формы, амплитуды и частоты (естественно, с теми ограничениями, которые накладывает аппаратная реализация калибратора). Контрольные вопросы 1. Чем измерительный сигнал отличается от сигнала? Приведите примеры измерительных сигналов, используемых в различных разделах науки и техники. 2. Перечислите признаки, по которым классифицируются измерительные сигналы. 3. Чем аналоговый, дискретный и цифровой сигналы отличаются друг от друга? 4. Расскажите о характеристиках и параметрах случайных сигналов. 5. Что такое помехи, как они классифицируются? Приведите примеры помех. 6. Какие типы математических моделей измерительных сигналов используются в метрологии? 7. Сколько и каких параметров нужно знать для описания каждого из элементарных измерительных сигналов? 8. Что такое амплитудная, частотная и фазовая модуляции? 9. Что такое амплитудно-импульсная, частотно-импульсная и широт-но-импульсная модуляции? 10. Дайте определение операции квантования. Где и каким образом она используется в метрологии? Что такое погрешность квантования? 11. Дайте определение дискретизации. Расскажите о том, как проводится дискретизация измерительных сигналов. Что утверждает теорема Котельникова? 12. Какие интегральные параметры используются для описания переменных сигналов? |
