Сергеев - Метрология. В. Г. Фирстов Кандидат физикоматематических наук
 Скачать 4.38 Mb. Скачать 4.38 Mb.
|
8.2. Однократные измеренияПрямые многократные измерения в большей мере относятся к лабораторным измерениям. Для производственных процессов более характерны однократные измерения. Однократные прямые измерения являются самыми массовыми и проводятся, если: при измерении происходит разрушение объекта измерения, отсутствует возможность повторных измерений, имеет место экономическая целесообразность. Эти измерения возможны лишь при определенных условиях: • объем априорной информации об объекте измерений такой, что модель объекта и определение измеряемой величины не вызывают сомнений; • изучен метод измерения, его погрешности либо заранее устранены, либо оценены; • средства измерений исправны, а их метрологические характеристики соответствуют установленным нормам. За результат прямого однократного измерения принимается полученная величина. До измерения должна быть проведена априорная оценка составляющих погрешности с использованием всех доступных данных. При определении доверительных границ погрешности результата измерений доверительная вероятность принимается, как правило, равной 0,95. Методика обработки результатов прямых однократных измерений приведена в рекомендациях МИ 1552—86 'ТСИ. Измерения прямые однократные. Оценивание погрешностей результатов измерений". Данная методика применима при выполнении следующих условий: составляющие погрешности известны, случайные составляющие распределены по нормальному закону, а неисключенные систематические, заданные своими границами 0,, — равномерно. Составляющими погрешности прямых однократных измерений являются: • погрешности СИ, рассчитываемые по их метрологическим характеристикам; • погрешность используемого метода измерений, определяемая на основе анализа в каждом конкретном случае; • личная погрешность, вносимая конкретным оператором. Если последние две составляющие не превышают 15% погрешности СИ, то за погрешность результата однократного измерения принимают погрешность используемого СИ. Данная ситуация весьма часто имеет место на практике. Названные составляющие могут состоять из неисключенных систематических и случайных погрешностей. При наличии нескольких систематических погрешностей, заданных своими границами ± i либо доверительными границами ± i(P), доверительная граница результата измерения соответственно может быть рассчитана по формуле 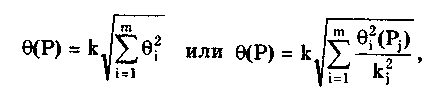 где i(Pj) — доверительная граница i-й неисключенной систематической погрешности, соответствующая доверительной вероятности Pj; kj — коэффициент, зависящий от Pj и определяемый так же, как и коэффициент k; k = k(m,P) — коэффициент, равный 0,95 при Р = 0,9 и 1,1 при Р = 0,95. При других доверительных вероятностях он определяется в соответствии с ГОСТ 8.207—76. Случайные составляющие погрешности результата измерений выражаются либо своими СКО Sxi, либо доверительными границами i(Р). В первом случае доверительная граница случайной составляющей погрешности результата прямого однократного измерения определяется через его СКО Sx:  где zp — точка нормированной функции Лапласа, отвечающей вероятности Р. При Р = 0,95 zf = 2. Если СКО Sxi определены экспериментально при небольшом числе измерений (n < 30), то в данной формуле вместо коэффициента zp следует использовать коэффициент Стьюдента, соответствующий числу степеней свободы i-й составляющей, оценка которой произведена при наименьшем числе измерений. В случае, когда случайные погрешности представлены доверительными границами ± ei(Рi), соответствующими разным доверительным вероятностям Рi, доверительная граница случайной погрешности результатов прямых однократных измерений 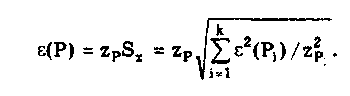 Найденные значения и (Р) используются для оценки погрешности результата прямых однократных измерений. В зависимости от соотношения и Sx суммарная погрешность определяется по одной из формул, приведенных в табл. 8.2. Значения коэффициента kp приведены в табл. 8.3. Тaблица 8.2 Формулы для расчета погрешности результата прямых однократных измерений (Р)
Таблица 8.3 Значение kr в зависимости от отношения 9/S, про доверительной вероятности 0,95
Кроме изложенного метода, суммирование случайных и систематических составляющих может проводиться и другими методами, ряд из которых рассмотрен в разд. 9.4. Результат прямых однократных измерений дол-жен записываться в соответствии с рекомендациями МИ 1317-86 в виде х ± (Р) при доверительной вероятности Р = Рд. Выше были рассмотрены прямые однократные измерения с точным оцениванием погрешностей, наиболее детально они проанализированы в [3]. В практике также имеют место прямые однократные измерения с приближенным оцениванием погрешности. Для них характерно оценивание погрешности полученного результата на основе метрологических характеристик, приведенных в нормативно-технической документации на используемые средства измерений. Поскольку эти характеристики относятся к любым экземплярам данного типа СИ, то у конкретного используемого средства действительные метрологические характеристики могут отличаться от нормированных. Прямые однократные измерения с приближенным оцениванием погрешностей правомочны, если доказана возможность пренебрежения случайной составляющей погрешности измерения, т.е. можно обосновано считать, что среднее квадратическое отклонение Sx случайной составляющей меньше 1/8 суммарной границы неисключенных систематических составляющих погрешности результата измерения. В простейшем случае, когда влияющие величины соответствуют нормальным условиям, погрешность результата прямого однократного измерения равна пределу основной погрешности средства измерения СИ, определяемой по нормативно-технической документации. Результат измерения запишется в виде = СИ. Доверительная вероятность не указывается, но, как правило, подразумевается, что она равна 0,96. При проведении измерений в условиях, отличных от нормальных, необходимо определять и учитывать пределы дополнительных погрешностей. Возможная методика суммирования основных и дополнительных погрешностей однократных измерений приведена в [3]. Пример 8.1. Оценить погрешность результата однократного измерения напряжения U = 0,9 В на сопротивлении R = 4 Ом, выполненного вольтметром класса точности 0,5 с верхним пределом измерения Uп = 1,5 В и внутренним сопротивлением Rv = 1000 Ом. Известно, что дополнительные погрешности показаний вольтметра из-за магнитного поля и температуры не превышают соответственно мп = 0,75% и т = 0,3% допускаемой предельной погрешности. Предел допускаемой относительной погрешности вольтметра на отметке 0,9 В составляет х = СИU0/U = 0,83%. При подсоединении вольтметра исходное напряжение U, изменится из-за наличия Rv и составит Тогда методическая погрешность, обусловленная конечным значением Rv, в относительной форме Данная погрешность является систематической и должна быть внесена в результат в виде поправки q = - m= 0,4 % или в абсолютной форме на отметке 0,9 В а= Uq/100 = 0,004 В. Тогда результат измерения с учетом поправки U = 0,9 + 0,004 = 0,904 В. Поскольку основная и дополнительная погрешности заданы своими граничными значениями, то они могут рассматриваться как неисключенные систематические погрешности и соответственно суммироваться. При доверительной вероятности 0,95 доверительная граница неисключенной систематической погрешности 8.3. Косвенные измеренияКосвенные измерения — это измерения, при которых искомое значение Q находят на основании известной зависимости (8.2) где Q1, Q2,...,Qm— значения, полученные при прямых измерениях. По виду функциональной зависимости F они делятся на две основные группы — линейные и нелинейные. Для линейных косвенных измерений математический аппарат статистической обработки полученных результатов разработан детально. Обработка результатов косвенных измерений [57] производится, как правило, методами: основанными на раздельной обработке аргументов и их погрешностей; линеаризации; приведения; йеребора. Первые три метода рассматриваются ниже, а четвертый — в [57]. Методика обработки результатов косвенных измерений приведена в документе МИ 2083-90 "ГСИ. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей". Косвенные измерения при, линейной зависимости между аргументами. Линейная функциональная зависимость является простейшей формой связи между измеряемой величиной и находимыми посредством прямых измерений аргументами. Она может быть выражена формулой где bi — постоянный коэффициент i-ro аргумента Qi; m — число аргументов. Погрешности линейных косвенных измерений оцениваются методом, основанным на раздельной обработке аргументов и их погрешностей. Если коэффициенты bi определяют экспериментально, то нахождение результата измерения величины Q производится поэтапно. Сначала оценивают каждое слагаемое biQi, как косвенно измеряемую величину, полученную в результате произведения двух измеряемых величин, а потом находят оценку измеряемой величины Q. Результат косвенного измерения определяют по формуле где Q̃i — оценка результата измерений аргумента Qi, получаемая, как правило, посредством обработки результатов многократных прямых измерений каждого из аргументов. При несмещенности и состоятельности результатов Q̃i полученная оценка результата измерения Q̃ будет также несмещенной и состоятельной. Поскольку дисперсия результата измерения то, если результаты Q̃i обладают минимальной дисперсией, т.е. являются эффективными, оценка результата измерения Q̃i также будет эффективной. При отсутствии корреляционной связи между аргументами СКО результата косвенного измерения S(Q̃), обусловленное случайными погрешностями, вычисляется по формуле 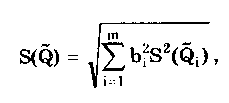 (8.3). (8.3).где S(Q̃i)— среднее квадратическое отклонение результата измерения аргумента qj, рассчитываемое по формуле (6.10). При наличии корреляционной связи между аргументами СКО результата косвенного измерения 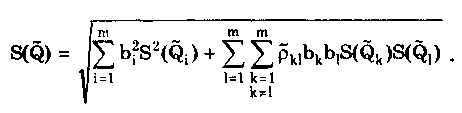 Здесь ρk1 — несмещенная оценка коэффициента корреляции между погрешностями аргументов Qk и Qi: 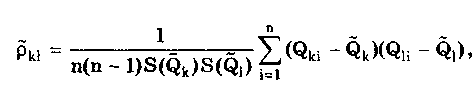 где Qki, Q1i — i-e результаты прямых измерений k-ro и i-го аргументов; n — число прямых измерений аргументов. Коэффициент корреляции может быть рассчитан и по другим формулам, равнозначным приведенной (см. разд. 9.3). Корреляция между аргументами чаще всего возникает в тех случаях, когда их измерения проводятся одновременно и подвергаются одинаковому влиянию внешних условий (температуры, влажности, напряжения питающей сети, помех и т.п.). Критерием отсутствия связи между двумя аргументами является выполнение неравенства [48] 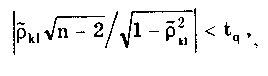 где tq— коэффициент Стьюдента, соответствующий уровню значимости q и числу степеней свободы n - 2. Необходимо проверить отсутствие корреляционных связей между всеми парными сочетаниями аргументов. Моделью для распределения результатов измерений отдельных аргументов обычно можно считать случайную величину с нормальным распределением. Для распределений, отличных от нормального, распределение среднего арифметического при этом все же можно считать нормальным [3]. Случайную погрешность результата косвенного измерения, образующуюся путем сложения случайных погрешностей результатов определения многих аргументов, еще с большим основанием можно считать нормально распределенной случайной величиной. Это дает возможность найти доверительный интервал для значения измеряемой величины. При большом числе измерений (более 25—30), выполненных при нахождении каждого из аргументов, доверительную границу случайной погрешности результата косвенного измерения можно определить по формуле где zp — квантиль нормального распределения, соответствующий выбранной доверительной вероятности Р. При меньшем числе измерений для определения доверительного интервала используется распределение Стьюдента, число степеней свободы которого рассчитывается по приближенной формуле [3] 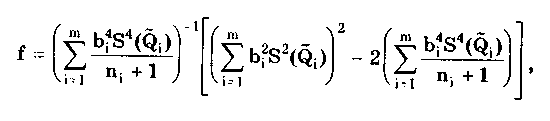 где ni — число измерений при определении аргумента Qi. В этом случае при условии, что распределение погрешностей результатов измерения аргументов не противоречит нормальному распределению, доверительная граница случайной погрешности результата косвенного измерения где tq — коэффициент Стьюдента, соответствующий доверительной вероятности P = l—q и числу степеней свободы f. Систематическая погрешность результата косвенного измерения определяется систематическими погрешностями результатов измерений аргументов. При измерениях последние стремятся исключить. Однако полностью это сделать не удается, всегда остаются неисключенные систематические погрешности, которые рассматриваются как реализации случайной величины [57], имеющей равномерное распределение. Такое предположение приводит обычно к достаточно осторожным заключениям о погрешности результатов косвенных измерений. Доверительные границы неисключенной систематической погрешности результата линейного косвенного измерения 9(Р) в случае, если неисключенные систематические погрешности аргументов заданы границами 0,, вычисляют по формуле 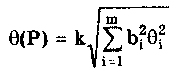 (8.4) (8.4)где k — поправочный коэффициент, определяемый принятой доверительной вероятностью Р и числом m составляющих i. Его значения приведены в табл. 8.4. Погрешность от применения этих усредненных коэффициентов не превышает 10% [57]. Таблица 8.4 Значения коэффициента k при m>4
Если число суммируемых слагаемых m 4 и они значительно различаются между собой, то значение коэффициента k определяется по табл. 8.5. Под L здесь понимают отношение наибольшей длины интервала (bi0i)max одного из слагаемых к длине bii остальных слагаемых. Таблица 8.5 Значения коэффициента k при m = 2. 3. 4
Если границы неисключенных систематических погрешностей результатов измерений аргументов заданы их доверительными границами i(Pi), соответствующими вероятностям Pi, то границу (Р) определяют по формуле 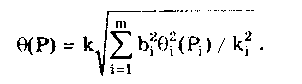 Коэффициенты ki определяются так же, как поправочный коэффициент k. Суммарная погрешность результата косвенного измерения оценивается на основе композиции распределений случайных и неисключенных систематических погрешностей. Формулы для ее расчета в зависимости от соотношения границ неисключенной систематической составляющей и СКО случайной составляющей погрешности приведены в табл. 8.6. Таблица 8.6 Погрешность результата косвенных измерений (Р)
Коэффициент kp определяется по табл. 8.7. Таблица 8.7. Зависимость kp от отношения q(P)/S(Q̃) при различной доверительной вероятности
Результат косвенных измерений должен записываться в виде х ± (Р) при доверительной вероятности Р. Косвенные измерения при нелинейной зависимости между аргументами. Для обработки результатов измерений при нелинейных зависимостях между аргументами и некоррелированных погрешностях используется метод линеаризации. Он состоит в том, что нелинейная функция, связывающая измеряемую величину с аргументами, разлагается в ряд Тейлора: Здесь 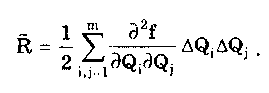 Метод линеаризации применим, если остаточным членом можно пренебречь. Это возможно в том случае, если 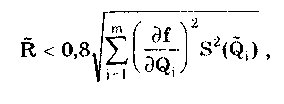 где S(Qi)— СКО случайной погрешности результата измерений аргумента Qi. При необходимости результаты косвенных измерений можно уточнить, используя члены ряда Тейлора более высокого порядка. Эти вопросы детально рассмотрены в [57]. Оценка результата определяется по формуле (8.6) Абсолютная погрешность косвенного измерения = Q̃ - Q , как это следует из уравнения (8.5), равна 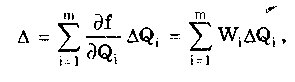 где Wi = ∂f/∂Qi — коэффициенты влияния i-го аргумента; Q, — абсолютная погрешность измерения i-го аргумента; WiQi — частная i-я погрешность определения результата косвенного измерения. Пример 8.2. Разложить в ряд Тейлора уравнение для определения плотности и получить выражение для расчета абсолютной погрешности. Плотность твердого тела р определяется как отношение результата измерения его массы m к объему V. При этом в соответствии с (8.5) получаем выражение 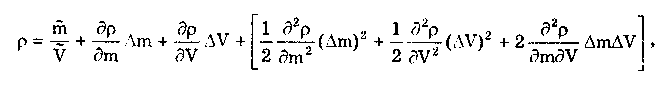 где в скобках стоит остаточный член. Учитывая, что 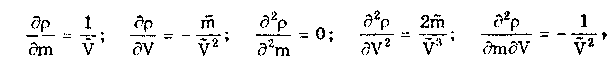 окончательно получим 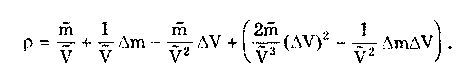 Абсолютная погрешность Коэффициенты влияния чаще всего определяются путем подстановки в выражения для частных производных оценок Q;. Поэтому вместо самих коэффициентов влияния получаются их оценки. В ряде случаев они устанавливаются экспериментально, что приводит к возникновению еще одной погрешности нелинейных косвенных измерений. Этой погрешности можно избежать, если зависимость (8.1) имеет вид (8.7) Тогда коэффициенты влияния Оценка измеряемой величины находится по (8.6), (8.7), а ее относительная погрешность с учетом последних формул определяется как 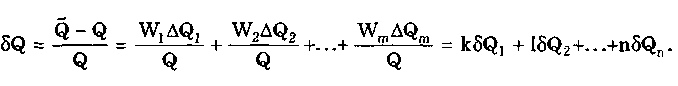 Из полученной формулы видно, что коэффициенты влияния для относительной погрешности оказываются равными показателям степеней соответствующих аргументов. Последние известны точно, и отмеченная выше погрешность не возникает. Для рассмотренного выше примера измерения плотности тела имеем ρ = m - V . Оценка СКО случайной погрешности результата косвенного измерения 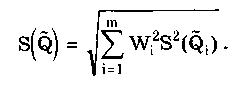 (8.8) (8.8)При точно известных коэффициентах влияния оно совпадает с уравнением (8.3), полученным для линейных косвенных измерений. Для зависимости вида (8.7) данная оценка, представленная в относительной форме, запишется в виде 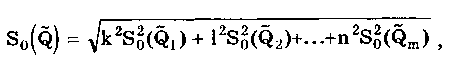 где Доверительные границы случайной погрешности результата при нормально распределенных погрешностях измерений аргументов вычисляются так же, как и для линейных косвенных измерений, при условии, что вместо коэффициентов bi в формулах подставляются коэффициенты влияния Wi. Аналогичным образом поступают при определении границ неисключенной систематической погрешности. Погрешность результата нелинейных косвенных измерений оценивается так же, как и при линейных измерениях. Метод приведения. Он используется для определения результатов косвенного измерения и его погрешности при наличии корреляции между погрешностями измерений аргументов. Метод можно также применять при неизвестных распределениях погрешностей аргументов. Он предполагает наличие ряда согласованных результатов измерений аргументов Q11, Q12, …, Qlm; Q21,… Q2m, Qj2, ..., Qjm; QL1, QL2, …, QLm, полученных в процессе многократных измерений. Согласованность результатов измерений означает либо одновременное их осуществление, либо то, что они выполнены над одним и тем же объектом и в одних и тех же условиях. Метод основан на приведении отдельных значений косвенно измеряемой величины к ряду простых измерений. Получаемые сочетания отдельных аргументов подставляют в формулу (8.6) и вычисляют отдельные значения измеряемой величины Q: Q1, Q2, ..., Qj, QL. Результат косвенного измерения Q̃ и СКО его случайной погрешности вычисляются по формулам 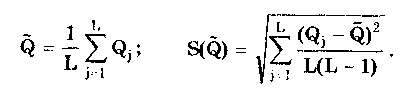 Доверительные границы случайной погрешности результата измерения рассчитываются по формуле = TS(Q̃), где Т — коэффициент, зависящий от вида распределения отдельных значений определяемой величины и выбранной доверительной вероятности. При нормальном распределении отдельных значений измеряемой величины доверительные границы случайных погрешностей вычисляются по методике для прямых многократных измерений, изложенной в ГОСТ 8.207-76. Границы неисключенной систематической погрешности и до верительные границы погрешности результата косвенного измерения определяются так же, как и в рассмотренных выше случаях. 8.4. Совместные и совокупные измеренияЭти виды измерений характеризуются тем, что значения искомых величин рассчитывают по системе уравнений, связывающих их с некоторыми другими величинами, определяемыми посредством прямых или косвенных измерений. При этом измеряются несколько комбинаций значений указанных величин. Каждая такая комбинация позволяет получить одно уравнение, а система содержит всю информацию о значениях искомых величин и имеет вид где F; — символ функциональной зависимости между величинами в i-м опыте; i=1; 2;...; n; n — число опытов; Qj — значения искомых величин, общее число которых равно m; Хг(i) — полученные в i-м опыте значения k величин, измеряемых прямыми или косвенными методами. Если Qi являются значениями одной и той же величины, то измерения называются совокупными, если разных физических величин, — то совместными. После подстановки в исходную систему уравнений результатов Хr(i) прямых или косвенных измерений и проведения необходимых преобразований получим n уравнений, содержащих лишь искомые величины и числовые коэффициенты: Такие уравнения называют условными. Для того чтобы рассчитать значения искомых величин, достаточно иметь m уравнений, т.е. столько же, сколько содержится неизвестных. Тогда результаты измерений и доверительные границы их погрешностей можно найти методами обработки результатов косвенных измерений. Однако обыкновенно для уменьшения погрешностей результатов измерений делается значительно больше измерений, чем это необходимо для определения неизвестных, т.е. n > m. Вследствие ограниченной точности определения величин Хг условные уравнения одновременно не обращаются в тождества ни при каких значениях искомых величин. И поскольку найти истинные значения искомых величин невозможно, то задача сводится к нахождению их оценок, представляющих собой наилучшие приближения к истинным значениям. Предположим, что Q̃j , где j =1, 2, ..., m, наилучшие приближения к неизвестным Qj. Если значения этих оценок подставить в условные уравнения, то их правые части будут отличаться от левых. Для получения тождеств нужно записать: где vi — величины, называемые остаточными погрешностями условных уравнений. Если в систему условных уравнений подставить истинные значения искомых величин, то остаточные погрешности превратятся в случайные погрешности условных уравнений. Одним из наиболее общих способов отыскания оценок истинных значений измеряемых величин является регрессионный анализ, или, как его часто называют, метод наименьших квадратов. Согласно ему оценки Q}выбираются так, чтобы минимизировать сумму квадратов остаточных погрешностей условных уравнений. Сумма квадратов остаточных погрешностей, определенных в соответствии с системой условных уравнений (8.9), составляет 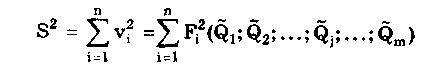 и достигает минимума при системе значений Qj, обращающей в нуль все частные производные от S2 по искомым величинам: Выражая остаточные погрешности через функции, стоящие в левой части условных уравнений, получаем систему из m уравнений с m неизвестными: 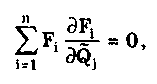 где j = l, 2,..., m, которая может быть решена относительно оценок qj искомых величин. При решении задачи в общем случае, когда условные уравнения нелинейны, а результаты отдельных измерений коррелированы, иногда возникает ряд непреодолимых трудностей. Задача относительно несложно решается лишь тогда, когда условные уравнения линейны или приведены к линейным известными способами и при отсутствии корреляции между результатами отдельных наблюдений. Ее решение подробно рассмотрено в [3]. Оценки, даваемые методом наименьших квадратов, являются состоятельными и несмещенными, а при нормальном распределении результатов измерений и эффективными. Детальное описание процесса обработки результатов совокупных и совместных измерений приведено в [12, 24]. Контрольные вопросы 1. Что такое вариационный ряд и интервалы группирования? Как определяется число интервалов группирования? 2. Что такое гистограмма, полигон и кумулятивная кривая? 3. Перечислите этапы обработки результатов прямых многократных измерений. 4. Для чего необходимо идентифицировать форму закона распределения результатов измерений? Расскажите, каким образом это делается. 5. Напишите алгоритм обработки результатов однократных измерений с точным оцениванием погрешностей. 6. Как обрабатываются результаты линейных косвенных измерений? 7. В чем состоит метод линеаризации и как он используется для обработки результатов нелинейных косвенных измерений? 8. Напишите алгоритм обработки результатов косвенных измерений при использовании метода приведения. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
