Сергеев - Метрология. В. Г. Фирстов Кандидат физикоматематических наук
 Скачать 4.38 Mb. Скачать 4.38 Mb.
|
6.3. Основные законы распределения6.3.1. Общие сведенияИспользование на практике вероятностного подхода к оценке погрешностей результатов измерений прежде всего предполагает знание аналитической модели закона распределения рассматриваемой погрешности. Встречающиеся в метрологии распределения достаточно разнообразны. В качестве примера можно привести результаты исследований [4] 219 фактических распределений погрешностей, имеющих место при измерении электрических и неэлектрических величин разнообразными приборами. Установлено, что примерно 50% распределений принадлежат к классу экспоненциальных, 30% являются уплощенными, а остальные 20% — различными видами двухмодальных распределений. Множество законов распределения случайных величин, используемых в метрологии, целесообразно классифицировать [4] следующим образом: • трапецеидальные (плосковершинные) распределения; • уплощеные (приблизительно плосковершинные) распределения; • экспоненциальные распределения; • семейство распределений Стьюдента; • двухмодальные распределения. 6.3.2. Трапецеидальные распределенияК трапецеидальным распределениям относятся: равномерное, собственно трапецеидальное и треугольное (Симпсона). Равномерноe распределение (рис. 6.5,а) описывается уравнением 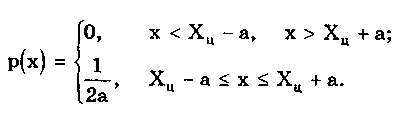 Трапецеидальное распределение (рис. 6.5, б) образуется как композиция двух равномерных распределений шириной а1 и а2, (рис. 6.2): 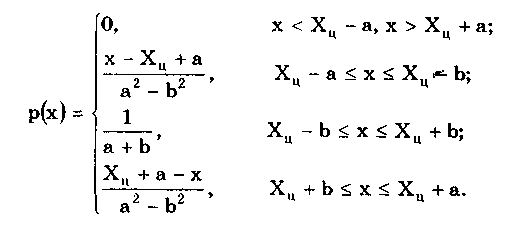 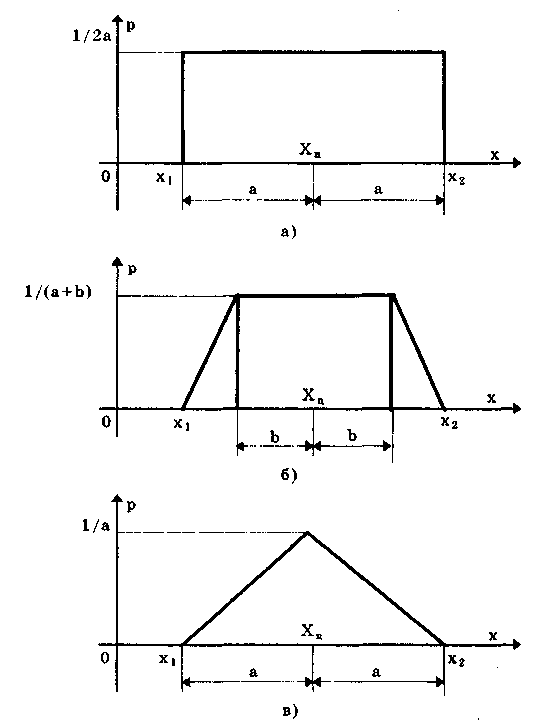 Рис. 6.5. Распределения: а — равномерное; б — трапецеидальное; в — треугольное (Симпсона) Треугольное (Симпсона) распределение (рис. 6.5, в) — это частный случай трапецеидального, для которого размеры исходных равномерных распределений одинаковы: а1 = а2(см. рис. 6.2): 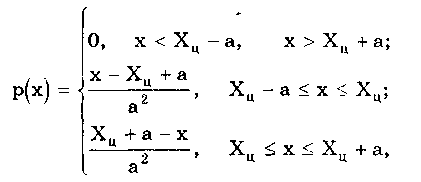 где Хц, а, b — параметры распределения. Математическое ожидание всех трапецеидальных распределений Хц = (x1 + х2) / 2. Медианы из соображений симметрии равны МО. Равномерное и собственно трапецеидальное распределения моды не имеют, а мода треугольного равна 1/а. Среднее квадратическое отклонение в зависимости от распределения определяется по формуле: • равномерное • трапецеидальное • треугольное Из приведенных уравнений следует, что СКО трапецеидальных распределений возрастает в 1,41 раза с ростом параметра b от нуля (треугольное) до а (равномерное). Коэффициент асимметрии всех трапецеидальных распределений равен нулю. Числовые параметры трапецеидальных распределений при различных отношениях ширины исходных равномерных распределений приведены в табл. 6.2. Таблица 6.2 Значения параметров трапецеидальных распределений
Равномерное распределение имеют погрешности: квантования в цифровых приборах, округления при расчетах, отсчета показаний стрелочного прибора, от трения в стрелочных приборах с креплением подвижной части на кернах или подпятниках, определения момента времени для каждого из концов временного интервала при измерении частоты и периода методом дискретного счета. Суммируясь между собой, эти погрешности образуют трапецеидальные распределения с различными отношениями сторон. 6.3.3. Экспоненциальные распределенияЭкспоненциальные распределения описываются формулой [4] 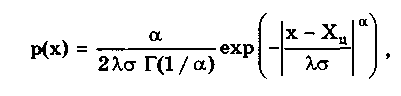 (6.5) (6.5)где 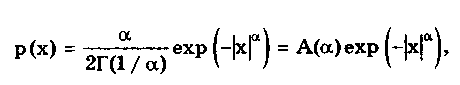 где А(а) — нормирующий множитель распределения. Интегральная функция нормированного экспоненциального распределения описывается выражением 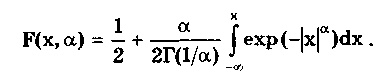 Интеграл, входящий в эту формулу, выражается через элементарные функции только при = 1/n, n = 1; 2; 3; ... При = n = 2; 3; 4; ... он может быть рассчитан по приближенным формулам, приведенным в [53]. Эксцесс и энтропийный коэффициент экспоненциальных распределений соответственно определяются по формулам: 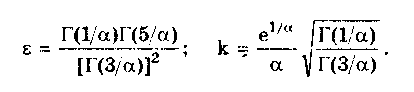 Анализ приведенных выражений показывает, что константа а однозначно определяет вид и все параметры распределений. При < 1 распределение имеет очень пологие спады и по форме близко к распределению Коши. При = 1 получается распределение Лапласа р(х) = 0,5е-|x| , при = 2 — нормальное распределение или распределение Гаусса. При > 2 распределения, описываемые формулой (6.5), близки по свойствам к трапецеидальным. При очень больших значениях формула (6.5) описывает практически равномерное распределение. В табл. 6.3 приведены параметры некоторых из экспоненциальных распределений. Таблица 6.3 Значения параметров экспоненциальных распределений при различных показателях a
6.3.4. Нормальное распределение (распределениеГаусса)Наибольшее распространение получил нормальный закон распределения, называемый часто распределением Гаусса: 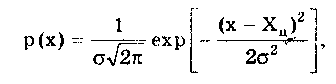 (6.6) (6.6)где — параметр рассеивания распределения, равный СКО; Хц — центр распределения, равный МО. Вид нормального распределения показан на рис. 6.3. 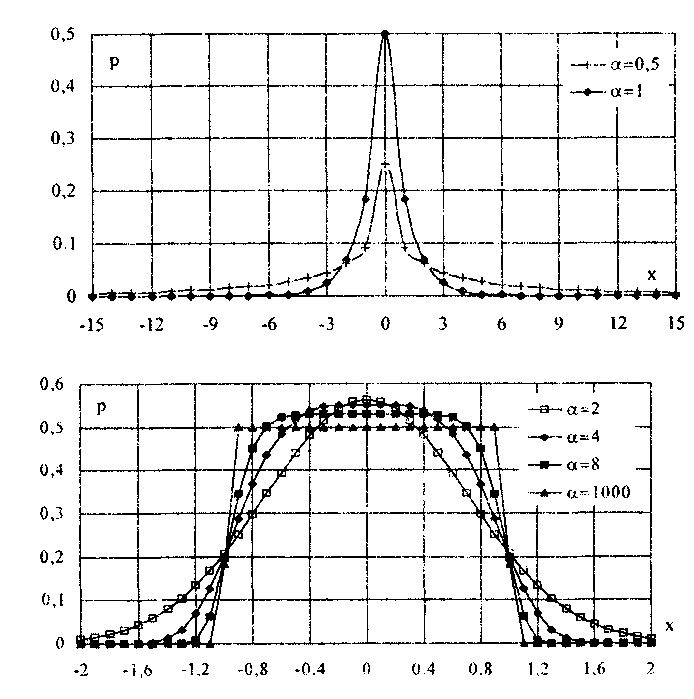 Рис. 6.6. Экспоненциальные распределения, определяемые по формуле (6.5) при = 1 и Хц = 0 Широкое использование нормального распределения на практике объясняется центральной предельной георемой теории вероятностей [48, 49], утверждающей, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдений формируются под действием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных. Вид экспоненциальных распределений при различных значениях показателя а приведен на рис. 6.6. При введении новой переменной t = (х-Хц)/ из (6.6) получается нормированное нормальное распределение, интегральная и дифференциальная функции которого соответственно равны: 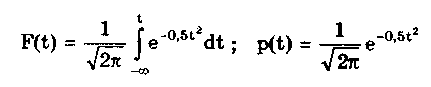 Нормирование приводит к переносу начала координат в центр распределения и выражению абсциссы в долях СКО. Значения интегральной и дифференциальной функций нормированного нормального распределения сведены в таблицы, которые можно найти в литературе по теории вероятностей [48, 49]. Определенный интеграл с переменным верхним пределом 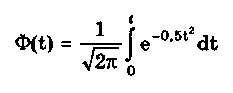 (6.7) (6.7)называют функцией Лапласа. Для нее справедливы следующие равенства: Ф(- ) = - ,5; Ф(0) = 0; Ф(+ ) = 0,5; Ф(t) = -Ф(t). Функция Лапласа используется для определения значений интегральных функций нормальных распределений. Функция F(t) связана с функцией Лапласа формулой F(t) = 0,5 + Ф(t). Поскольку интеграл в (6.7) не выражается через элементарные функции, то значения функции Лапласа для различных значений t сведены в таблицу (см. приложение 1). 6.3.5. Уплощенные распределенияДанные распределения представляют собой композицию равномерного и какого-либо экспоненциального распределения (см. рис. 6.2). Вид одного из них показан на риc. 6.7. Уплощенные распределения отличаются от экспоненциальных с показателем >2 тем, что при почти плоской вершине имеют длинные, медленно спадающие "хвосты", в то время как экспоненциальные распределения при >> 2 обрываются тем круче, чем более плоской является их вершина. 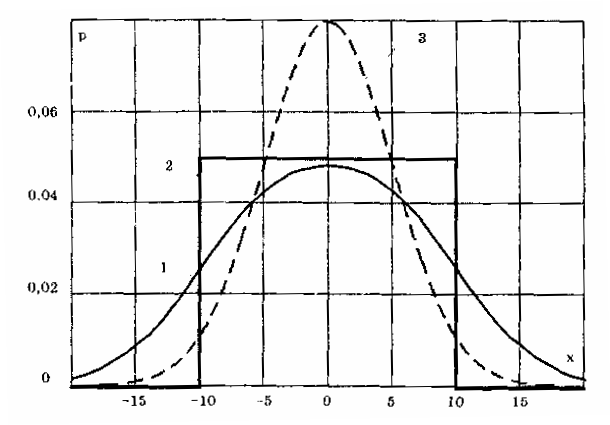 Рис. 6.7. Уплощенное распределение (1), полученное как композиция равномерного (2) и нормального (3) распределений с СКО, равными Основными параметрами, определяющими форму таких распределений, являются: • показатель относительного содержания в композиции равномерной составляющей Ср= Ор/стэк(., где ар, оэкс — СКО равномерного и экспоненциального распределений; • показатель а экспоненциальной составляющей. Вес относительной дисперсии 2экс в суммарной дисперсии (экс2 + р2), как правило, не превышает 10%. Однако его влияние на форму кривой р(х) будет значительным. Другая особенность уплощенных распределений: при том же значении эксцесса энтропийный коэффициент у них существенно меньше, чем у экспоненциальных распределений. 6.3.6. Семейство распределений СтъюдентаЭти законы описывают плотность распределения вероятности среднего арифметического, вычисленного по выборке из п случайных отсчетов нормально распределенной генеральной совокупности. Распределения Стьюдента нашли широкое применение при статистической обработке результатов многократных измерений. Их вид зависит от числа отсчетов n, по которым находится среднее арифметическое значение, поэтому и говорят о семействе законов, В центрированном и нормированном виде они описываются формулой 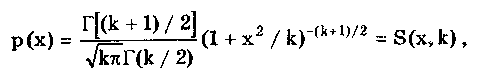 где k — число степеней свободы, зависящее от числа п усредняющих отсчетов: k = n-1. Вид распределения Стьюдента для различных значений k показан на рис. 6.8. При увеличении k распределение Стьюдента переходит в распределение Гаусса. 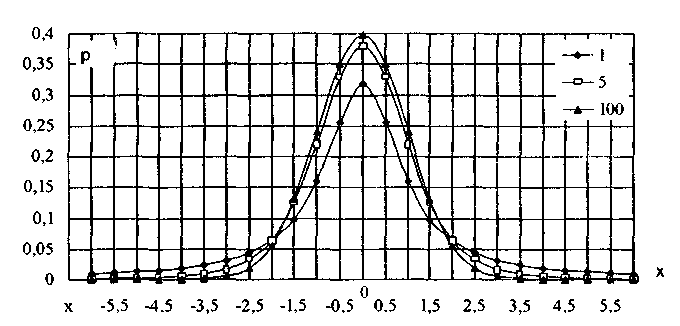 Рис. 6.8. Распределение Стьюдента при степенях свободы, равных 1 (распределение Коши), 5 и 100 Для нормированных распределений Стьюдента с k > 4 справедливы следующие соотношения: 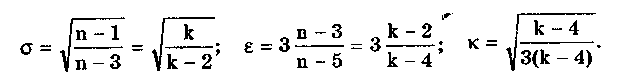 Значения некоторых параметров для различных степеней свободы приведены в табл. 6.4. Таблица 6.4 Значение точечных оценок распределения Стьюдента при различных степенях свободы k
Распределения Стьюдента имеют ряд особенностей: • при n < 3 их СКО становится равным бесконечности, т.е. дисперсионная оценка ширины разброса не работает (перестает существовать); • классический аппарат моментов для оценки формы и ширины распределения Стьюдента с малым числом степеней свободы оказывается не работоспособным, и их ширина и форма могут быть оценены лишь с использованием доверительных и энтропийных оценок. ch-им распределение Стьюдента резко отличается от других распределений. Разновидностью распределения Стьюдента является распределение Коши. Оно важно тем, что ему подчиняется распределение отношения двух нормально распределенных центрированных случайных величин. Распределение Коши — это предельное распределение семейства законов Стьюдента с минимально возможным числом степеней свободы, равным k = 1 (рис. 6.8): 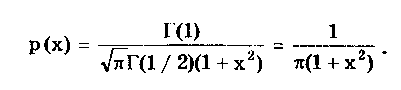 В общем виде (не нормированном и не центрированном) распределение Коши имеет вид 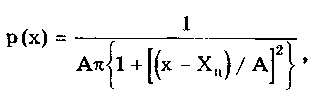 где А, Хц — параметры распределения. Свойства распределения Коши резко отличаются от свойств экспоненциальных распределений, а именно: • дисперсия и СКО не существуют, так как определяющий их интеграл расходится. Они будут бесконечно увеличиваться при росте числа экспериментальных данных. Оценка ширины распределения может быть произведена только на основе теории информации; • оценка центра в виде среднего арифметического для распределения Коши неправомочна, так как ее рассеяние • математическое ожидание не существует; • для определения Хц необходимо использовать медиану; • эксцесс равен бесконечности, а контрэксцесс равен нулю; • энтропийное значение погрешности равно 2А. 6.3.7. Двухмодальные распределенияК ним относятся дискретное двузначное, арксинусоидальное и двухмодальные остро- и кругловершинные распределения. Дискретное двузначное распределение — это распределение, при котором с равными вероятностями встречаются только два значения случайной величины. В центрированном виде (рис. 6.9) оно описывается формулой где (х) — дельта-функция Дирака; ±А — возможные значения случайной величины. При дискретном двузначном распределении СКО равно значению параметра А, = 1, к = 1, k = 0. 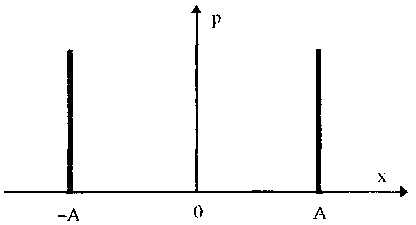 Рис. 6.9. Дискретное двузначное распределение Дискретное двузначное распределение может быть приближенно предcтавлено в виде суммы двух нормальных распределений с одинаковыми по модулю, но противоположными по знаку МО и при стремлении r нулю их СКО: 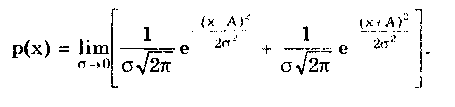 Арксинусоидальное распределение (рис. 6.10) описывается выражением: где А — параметр распределения. Его СКО равно 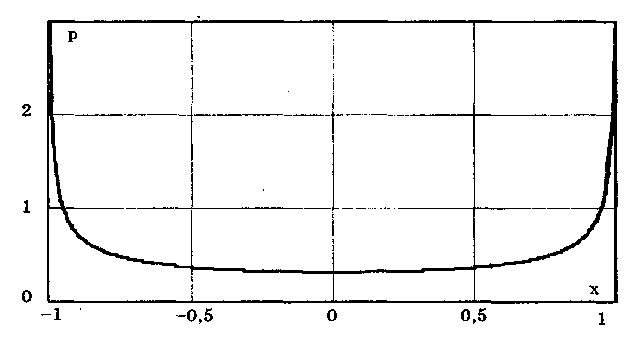 Рис. 6.10. Арксинусоидальное распределение при А = 1 Остро- и кругловершинные двухмодальные распределения получаются как композиция дискретного двузначного и экспоненциального распределений с различными значениями коэффициента а (рис. 6.11). При < 2 получаются островершинные, при > 2 — кругловершинные распределения. 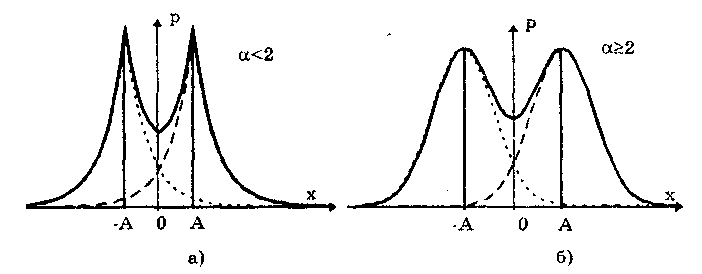 Рис. 6.11. Островершинные (а) и кругловершинные (б) двухнедельные распределения Основными параметрами таких распределений являются: • показатель относительного содержания в композиции дискретной составляющей Сд= д /экс= А/экс, где д и экс — СКО дискретного и экспоненциального распределений. Как правило, Сд (0;2) . Чем больше показатель Сд, тем больше провал. При Сд = 0 провал на графике распределения отсутствует; • показатель степени для экспоненциальных распределений, который обычно лежит в пределах от 0,5 до 2. Островершинные распределения получаются при использовании некоторых высокоточных цифровых вольтметров, а кругловершинные распределения имеют погрешности от механического гистерезиса элементов приборов и датчиков. 6.4. Точечные оценки законов распределенияРассмотренные выше функции распределения описывают поведение непрерывных случайных величин, т.е. величин, возможные значения которых неотделимы друг от друга и непрерывно заполняют некоторый конечный или бесконечный интервал. На практике все результаты измерений и случайные погрешности являются величинами дискретными, т.е. величинами Xj, возможные значения которых отделимы друг от друга и поддаются счету. При использовании дискретных случайных величин возникает задача нахождения точечных оценок параметров их функций распределения на основании выборок — ряда значений хи принимаемых случайной величиной х в п независимых опытах. Используемая выборка должна быть репрезентативной (представительной), т.е. должна достаточно хорошо представлять пропорции генеральной совокупности. Оценка параметра называется точечной, если она выражается одним числом. Задача нахождения точечных оценок — частный случай статистической задачи нахождения оценок параметров функции распределения случайной величины на основании выборки. В отличие от самих параметров их точечные оценки являются случайными величинами, причем их значения зависят от объема экспериментальных данных, а закон распределения — от законов распределения самих случайных величин. Точечные оценки могут быть состоятельными, несмещенными и эффективными. Состоятельной называется оценка, которая при увеличении объема выборки стремится по вероятности к истинному значению числовой характеристики. Несмещенной называется оценка, математическое ожидание которой равно оцениваемой числовой характеристике. Наиболее эффективной считают ту из нескольких возможных несмещенных оценок, которая имеет наименьшую дисперсию. Требование несмещенности на практике не всегда целесообразно, так как оценка с небольшим смещением и малой дисперсией может оказаться предпочтительнее несмещенной оценки с большой дисперсией. На практике не всегда удается удовлетворить одновременно все три этих требования, однако выбору оценки должен предшествовать ее критический анализ со всех перечисленных точек зрения. Наиболее распространенным методом получения оценок является метод наибольшего правдоподобия [4, 48], который приводит к асимптотически несмещенным и эффективным оценкам с приближенно нормальным распределением. Среди других методов можно назвать методы моментов [24] и наименьших квадратов. Точечной оценкой МО результата измерений является среднее арифметическое значение измеряемой величины (6.8) При любом законе распределения оно является состоятельной и несмещенной оценкой, а также наиболее эффективной по критерию наименьших квадратов. Точечная оценка дисперсии, определяемая по формуле 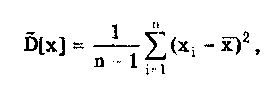 (6.9) (6.9)является несмещенной и состоятельной. СКО случайной величины х определяется как корень квадратный из дисперсии. Соответственно его оценка может быть найдена путем извлечения корня из оценки дисперсии. Однако эта операция является нелинейной процедурой, приводящей к смещенности получаемой таким образом оценки. Для исправления оценки СКО вводят поправочный множитель k(n), зависящий от числа наблюдений n. Он изменяется от k(3) = 1,13 до k() 1,03. Оценка среднего квадратического отклонения 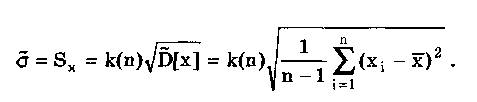 Полученные оценки МО и СКО являются случайными величинами. Это проявляется в том, что при повторениях серий из n наблюдений каждый раз будут получаться различные оценки х̅ и ̃. Рассеяние этих оценок целесообразно оценивать с помощью СКО Sx̅ и S. Оценка СКО среднего арифметического значения 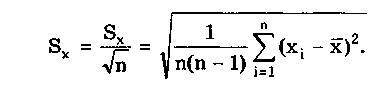 (6.10) (6.10) Оценка СКО [4, 48] среднего квадратического отклонения Отсюда следует, что относительная погрешность определения СКО может быть оценена [4] как Она зависит только от эксцесса и числа наблюдений в выборке и не зависит от СКО, т.е. той точности, с которой производятся измерения. Ввиду того, что большое число измерений проводится относительно редко, погрешность определения а может быть весьма существенной. В любом случае она больше погрешности из-за смещенности оценки, обусловленной извлечением квадратного корня и устраняемой поправочным множителем k(n). В связи с этим на практике пренебрегают учетом смещенности оценки СКО отдельных наблюдений и определяют его по формуле 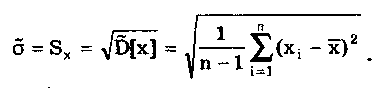 (6.11) (6.11)т.е. считают k(n) = l. Иногда оказывается удобнее использовать следующие формулы для расчета оценок СКО отдельных наблюдений и результата измерения: 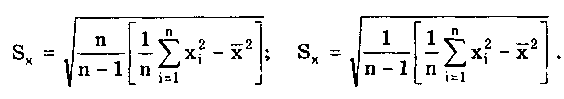 (6.12) (6.12)Точечные оценки других параметров распределений используются значительно реже. Оценки коэффициента асимметрии и эксцесса находятся по формулам [55] 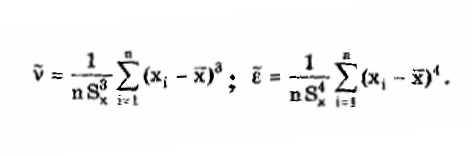 Определение рассеяния оценок коэффициента асимметрии и эксцесса описывается различными формулами в зависимости от вида распределения. Краткий обзор этих формул приведен в [4]. 6.5. Доверительная вероятность и доверительныйинтервалРассмотренные точечные оценки параметров распределения дают оценку в виде числа, наиболее близкого к значению неизвестного параметра. Такие оценки используют только при большом числе измерений. Чем меньше объем выборки, тем легче допустить ошибку при выборе параметра. Для практики важно не только получить точечную оценку, но и определить интервал, называемый доверительным, между границами которого с заданной дове рителъной вероятностью где q — уровень значимости; хн, хв— нижняя и верхняя границы интервала, находится истинное значение оцениваемого параметра. В общем случае доверительные интервалы можно строить на основе неравенства Чебышева. При любом законе распределения случайной величины, обладающей моментами первых двух порядков, верхняя граница вероятности попадания отклонения случайной величины х от центра распределения Хц в интервал tSx описывается неравенством Чебышева 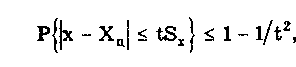 где Sx — оценка СКО распределения; t — положительное число. Для нахождения доверительного интервала не требуется знать закон распределения результатов наблюдений, но нужно знать оценку СКО. Полученные с помощью неравенства Чебышева интервалы оказываются слишком широкими для практики. Так, доверительной вероятности 0,9 для многих законов распределений соответствует доверительный интервал 1,6SX. Неравенство Чебышева дает в данном случае 3,16SX. В связи с этим оно не получило широкого распространения. В метрологической практике используют главным образом кван-тильные оценки доверительного интервала. Под 100P-процентным квантилем хр понимают абсциссу такой вертикальной линии, слева от которой площадь под кривой плотности распределения равна Р%. Иначе говоря, квантиль — это значение случайной величины (погрешности) с заданной доверительной вероятностью Р. Например, медиана распределения является 50%-ным квантилем х0,5. На практике 25- и 75%-ный квантили принято называть сгибами, или квантилями распределения. Между ними заключено 50% всех возможных значений случайной величины, а остальные 50% лежат вне их. Интервал значений случайной величины х между х0 05 и х0 95 охватывает 90% всех ее возможных значений и называется интерквантильным промежутком с 90%-ной вероятностью. Его протяженность равна d0,9= х0,95 - х0,05. На основании такого подхода вводится понятие квантильных значений погрешности, т.е. значений погрешности с заданной доверительной вероятностью Р — границ интервала неопределенности ± Д = ± (хр - х1-р)/2 = ± dp/2. На его протяженности встречается Р% значений случайной величины (погрешности), a q = (1- Р)% общего их числа остаются за пределами этого интервала. Для получения интервальной оценки нормально распределенной случайной величины необходимо: • определить точечную оценку МО х̅ и СКО Sx случайной величины по формулам (6.8) и (6.11) соответственно; • выбрать доверительную вероятность Р из рекомендуемого ряда значений 0,90; 0,95; 0,99; • найти верхнюю хв и нижнюю хн границы в соответствии с уравнениями 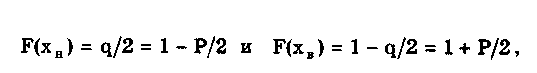 полученными с учетом (6.1). Значения хн и хв определяются из таблиц значений интегральной функции распределения F(t) или функции Лапласа Ф(1). Полученный доверительный интервал удовлетворяет условию 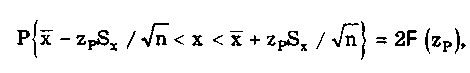 (6.13) (6.13)где n — число измеренных значений; zp — аргумент функции Лапласа Ф(1), отвечающей вероятности Р/2. В данном случае zp называется квантильным множителем. Половина длины доверительного интервала Пример 6.1. Произведено 50 измерений постоянного сопротивления. Определить доверительный интервал для МО значения постоянного сопротивления, если закон распределения нормальный с параметрами mx = R = 590 Ом, Sx= 90 Ом при доверительной вероятности Р = 0,9. Так как гипотеза о нормальности закона распределения не противоречит опытным данным, доверительный интервал определяется по формуле 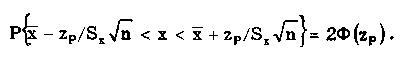 Отсюда Ф(zр) = 0,45. Из таблицы, приведенной в приложении 1, находим, что zp= 1,65. Следовательно, доверительный интервал запишется в виде При отличии закона распределения случайной величины от нормального необходимо построить его математическую модель и определять доверительный интервал с ее использованием. Рассмотренный способ нахождения доверительных интервалов справедлив для достаточно большого числа наблюдений n, когда = Sx. Следует помнить, что вычисляемая оценка СКО Sx является лишь некоторым приближением к истинному значению . Определение доверительного интервала при заданной вероятности оказывается тем менее надежным, чем меньше число наблюдений. Нельзя пользоваться формулами нормального распределения при малом числе наблюдений, если нет возможности теоретически на основе предварительных опытов с достаточно большим числом наблюдений определить СКО. Расчет доверительных интервалов для случая, когда распределение результатов наблюдений нормально, но их дисперсия неизвестна, т.е. при малом числе наблюдений п, возможно выполнить с использованием распределения Стьюдента S(t,k). Оно описывает плотность распределения отношения (дроби Стьюдента): 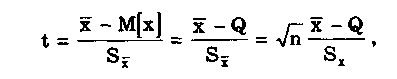 где Q — истинное значение измеряемой величины. Величины х̅, Sx. и Sx̅ вычисляются на основании опытных данных и представляют собой точечные оценки МО, СКО результатов измерений и СКО среднего арифметического значения. Вероятность того, что дробь Стьюдента в результате выполненных наблюдений примет некоторое значение в интервале (- tp; + tp) 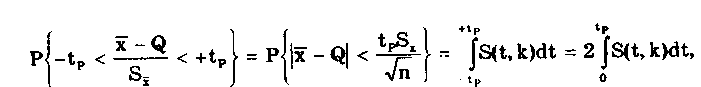 (6.14) где k — число степеней свободы, равное (п - 1). Величины tp (называемые в данном случае коэффициентами Стьюдента), рассчитанные с помощью двух последних формул для различных значений доверительной вероятности и числа измерений, табулированы (см. таблицу в приложении 1). Следовательно, с помощью распределения Стьюдента можно найти вероятность того, что отклонение среднего арифметического от истинного значения измеряемой величины не превышает В тех случаях, когда распределение случайных погрешностей не является нормальным, все же часто пользуются распределением Стьюдента с приближением, степень которого остается неизвестной. Распределение Стьюдента применяют при числе измерений n < 30, поскольку уже при n = 20, ...,30 оно переходит в нормальное и вместо уравнения (6.14) можно использовать уравнение (6.13). Результат измерения записывается в виде: Полученный результат измерения не является одним конкретным числом, а представляет собой интервал, внутри которого с некоторой вероятностью Рд находится истинное значение измеряемой величины. Выделение середины интервала х вовсе не предполагает, что истинное значение ближе к нему, чем к остальным точкам интервала. Оно может быть в любом месте интервала, а с вероятностью 1 - Рд даже вне его. Пример 6.2. Определение удельных магнитных потерь для различных образцов одной партии электротехнической стали марки 2212 дало следующие результаты: 1,21; 1,17; 1,18; 1,13; 1,19; 1,14; 1,20 и 1,18 Вт/кг. Считая, что систематическая погрешность отсутствует, а случайная распределена по нормальному закону, требуется определить доверительный интервал при значениях доверительной вероятности 0,9 и 0,95. Для решения задачи использовать формулу Лапласа и распределение Стьюдента. По формулам (6.8) в (6.11) находим оценки среднего арифметического значения и СКО результатов измерений. Они соответственно равны 1,18 и 0,0278 Вт/кг. Считая, что оценка СКО равна самому отклонению, находим: 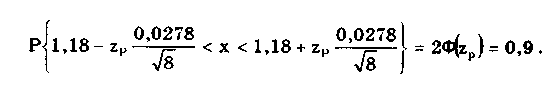 Отсюда, используя значения функции Лапласа, приведенные в таблице приложения 1, определяем, что zp= 1,65. Для Р = 0,95 коэффициент zp =1,96. Доверительные интервалы, соответствующие Р = 0,9 и 0,95, равны 1,18 ± 0,016 и 1,18±0,019 Вт/кг. В том случае, когда нет оснований считать, что СКО и его оценка равны, доверительный интервал определяется на основе распределения Стьюдента: 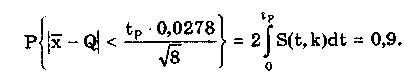 По таблице приложения 1 находим, что t0,9 = 1,9 и t0,95 = 2,37. Отсюда доверительные интервалы соответственно равны 1,18±0,019 и 1,18±0,023 Вт/кг. Контрольные вопросы. 1.При каких условиях погрешность измерения может рассматриваться как случайная величина? 2. Перечислите свойства интегральной и дифференциальной функций распределения случайной величины. 3. Назовите числовые параметры законов распределения. 4. Каким образом может задаваться центр распределения? 5. Что такое моменты распределения? Какие из них нашли применение в метрологии? 6. Назовите основные классы распределений, используемых в метрологии. 7. Дайте характеристику распределениям, входящим в класс трапецеидальных распределений. 8. Что такое экспоненциальные распределения? Каковы их свойства и характеристики? 9. Что такое нормальное распределение? Почему оно играет особую роль в метрологии? 10. Что такое функция Лапласа и для чего она используется? 11. Как описывается и где используется семейство распределений Стьюдента? 12. Какие точечные оценки законов распределения вы знаете? Какие требования предъявляются к ним? 13. Что такое доверительный интервал? Какие "способы его задания вам известны? |
