Теоретические основы технического обслуживания и ремонта электронного оборудования электронной части станков с ЧПУ. Курсовой. В области промышленной автоматизации в настоящее время для реализации приложений управления используются различные аппаратные и программные архитектуры и подходы
 Скачать 274.55 Kb. Скачать 274.55 Kb.
|
|
Определяем значение критерия Рейнольдса для принятого расчетного расхода из выражения: 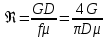 (2.5) (2.5)где f - площадь сечения трубопровода, м2; μ – динамический коэффициент вязкости, Па∙с. Для горючего газа и воздуха динамический коэффициент вязкости приведен в таблице 2.3, для воды и водяного пара - в таблице 2.4 Таблица 2.3 Физические параметры горючих газов и воздуха
Окончание таблицы 2.3
Таблица 2.4 Динамический коэффициент вязкости воды и водяного пара (µ·105 Па·с) Примечание: над чертой - вода, под чертой – пар
При определении численных значений динамического коэффициента вязкости следует применять линейное интерполирование. В первом приближении можно считать, что динамический коэффициент вязкости не зависит от давления, а определяется лишь одной температурой. С помощью табличных данных и метода интерполяции определяем значение динамического коэффициента вязкости. 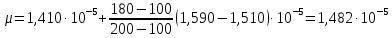 (2.6) (2.6)Отсюда получаем значение критерия Рейнольдса: 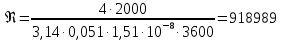 (2.7) (2.7)Выбираем максимальный расчетный перепад давления: 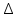 ∆𝑝=𝑝1−𝑝2 (2.8) ∆𝑝=𝑝1−𝑝2 (2.8)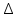 ∆𝑝=11−10,5=0,5МПа (2.9) ∆𝑝=11−10,5=0,5МПа (2.9)Определяем диаметр трубопровода при рабочей температуре t по уравнению: 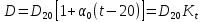 (2.10) (2.10)где α0 - средний коэффициент линейного теплового расширения материала трубопровода; Kt - поправочный множитель на тепловое расширение (значения Kt приведены в таблице 2.5). С помощью метода интерполяции определяем коэффициент Kt при температуре 190 ºС для стали Х23Н13. 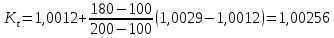 (2.11) (2.11)С учетом коэффициента Kt рассчитываем диаметр D: 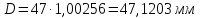 (2.12) (2.12)Таблица 2.5 Поправочный множитель Kt на тепловое расширение трубопровода и диафрагм
Диаметр расточки диафрагмы d определяем в следующей последовательности: -подсчитываем значение mα из соотношения: 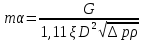 (2.13) (2.13)Величину 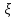 берут из таблицы 2.6 по подсчитанному значению ∆p/p1 принимая m=0,3 (в первом приближении). берут из таблицы 2.6 по подсчитанному значению ∆p/p1 принимая m=0,3 (в первом приближении).Сначала находим соотношение ∆p/p1: 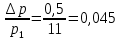 (2.14) (2.14) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
