Физкультур минутка по математики. V. Повторение пройденного материала. Работа в печатной тетради Задание 23
 Скачать 2.68 Mb. Скачать 2.68 Mb.
|
|
Задание № 55. Так как учащиеся еще незнакомы со знаками «>» и «<» , то оформить решение они должны так: 70 см равно 7 дм; 4 м меньше 51 дм; 95 см меньше 1 м; 6 дм 1 см больше 49 см. Задание № 56. Решение: нужно выбрать такую часть числового луча, на которой удобно отметить точки с заданными координатами, например так: 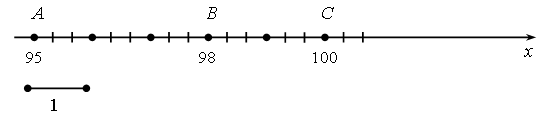 VI. Итог урока. – Что нового узнали на уроке? – Как определить название многоугольника? – Какие многоугольники называют выпуклыми? Невыпуклыми? – Как обозначить многоугольник на чертеже? Домашнее задание: № 18 (учебник). Урок 17 Сложение и вычитание вида 26 2, 26 10 Цели урока: познакомить учащихся с правилами поразрядного сложения и вычитания чисел в пределах 100; рассмотреть практическое выполнение действий с помощью цветных палочек; совершенствовать вычислительные навыки; практическим путем находить значение умножения и деления; развивать внимание и логическое мышление. Ход урока I. Организационный момент. II. Устный счет. 1. Вставьте числа в пустые клетки квадрата так, чтобы сумма по всем направлениям была одинаковой.
2. На каком рисунке больше треугольников – на левом или на правом? 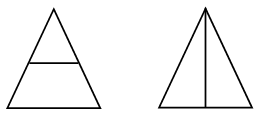 3. Решите задачу. Вова ищет друзей, которые спрятались от него. Вдруг он заметил, что из-под забора видны 8 ног. Сколько детей стоит за забором? 4. Игра «Парашютисты». – Куда должен приземлиться каждый из парашютов? 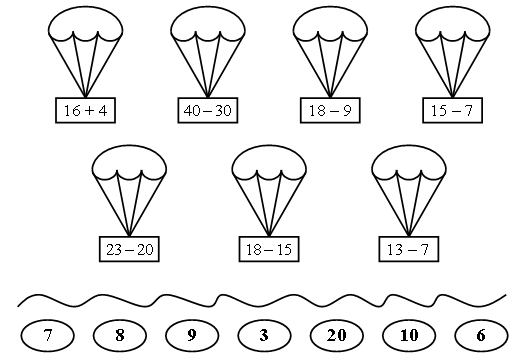 5. Винни-Пух толще Кролика, Кролик толще Пятачка. Кто тоньше всех? 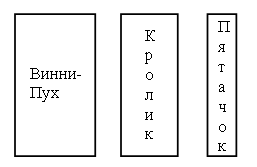 III. Сообщение темы урока. – Рассмотрите выражения, записанные на доске:
– Значения каких выражений вы не сможете еще вычислить? – Сегодня мы узнаем, как выполнить сложение и вычитание вида 26 2 и 26 10. IV. Изучение нового материала. В учебнике показано, как с помощью цветных палочек познакомить второклассников с правилами поразрядного сложения и вычитания чисел в пределах 100. Оранжевая палочка обозначает десяток, а белая – единицу. Необходимо построить работу таким образом, чтобы при рассмотрении каждого примера дети, выкладывая палочки, повторяли способы действия Волка и Зайца. При этом школьники могут работать в парах. Задание № 1 (с. 40). Пример 1. Учитель ставит перед детьми учебную задачу: используя цветные палочки, найти способ сложения чисел 26 и 2. – Рассмотрите первый рисунок на с. 40 учебника и выскажите свои предположения. (В числе 26 – два десятка и шесть единиц, поэтому Волк составил «поезд» из 2 оранжевых и 6 белых «вагонов».) – Составьте такой же «поезд» из своих палочек. – Объясните, что делает Заяц. (Заяц прицепляет к белым «вагонам» еще 2 белых «вагона», так как надо прибавить 2 единицы.) – Выполните это действие на своих палочках. – Что у вас получилось? (Получился «поезд», в котором 2 оранжевых и 8 белых «вагонов» (6 + 2 = 8.) – Какое число обозначает этот поезд? (Он обозначает число 28.) Учащиеся подводят итог: сумма 26 и 2 есть число, в котором 2 десятка, а единиц 6 и 2, всего 8. Значит, 26 + 2 = 28. Пример 2. Постановка задачи: необходимо вычесть 2 из 26, используя цветные палочки. Снова составим «поезд» из 2 оранжевых и 6 белых «вагонов». По рисунку видно, что, вычитая 2, Волк предложил отцепить 2 белых «вагона». Получился «поезд», в котором 2 оранжевых и 4 белых «вагона» (6 – 2 = 4). Он обозначает число 24. Итак, разность 26 и 2 есть число, в котором 2 десятка, а единиц 6 без 2, то есть 4. Значит, 26 – 2 = 24. Пример 3. Постановка задачи: сложить 26 и 10. Рассматриваем рисунок: Волк составил «поезд» из 2 оранжевых и 6 белых «вагонов». Так как 10 – это один десяток, то Заяц к оранжевым «вагонам» прицепляет еще 1 оранжевый «вагон». Получился «поезд», в котором 3 оранжевых (2 + 1 = 3) и 6 белых (6 + 0 = 6) «вагонов». Он обозначает число 36. Значит, 26 + 10 = 36. Пример 4. Постановка задачи: вычесть 10 из 26. Составим «поезд» из 2 оранжевых и 6 белых «вагонов». Отцепим от оранжевых «вагонов» один. Получился «поезд», в котором 1 оранжевый (2 – 1 = 1) и 6 белых (6 – 0 = 6) «вагонов». Он обозначает число 16. Значит, 26 – 10 = 16. В заключение учитель просит сформировать правило: как же, не используя цветные палочки, можно складывать и вычитать двузначные числа. – Прочитайте правила, приведенные на с. 41 учебника. Задание № 2 (с. 41). Учащиеся работают в парах; используя цветные палочки, они выполняют сложение и вычитание двузначных чисел. Задание № 3 (с. 41). Выполнить это задание учащиеся должны уже без цветных палочек, руководствуясь правилами, сформулированными при объяснении нового материала. Рассмотрим способы рассуждения на примерах. 1) 29 – 8. При вычитании чисел из единиц вычитают единицы, а из десятков – десятки. В числе 29 – девять единиц, а в числе 8 – восемь единиц. Вычитаем: 9 – 8 = 1. Значит, в результате получится одна единица. В числе 29 – два десятка, а в числе 8 – нуль десятков. Значит, в результате будет два десятка. Следовательно, 29 – 8 = 21. 2) 20 + 1. При сложении чисел единицы складываются с единицами, а десятки – с десятками. В числе 20 – нуль единиц, а в числе 1 – одна единица. Складываем: 0 + 1 = 1. Значит, в результате будет одна единица. В числе 20 – два десятка, а в числе 1 – нуль десятков. Значит, в результате будет два десятка. Следовательно, 20 + 1 = 21. Аналогично дети рассуждают в остальных случаях.  V. Повторение пройденного материала. 1. Работа по учебнику. Задание № 11 (с. 43). Запись: 13, 31, 49, 66, 90, 100; 100, 90, 66, 49, 31, 13. Задание № 12 (с. 43). – Какое действие необходимо выполнить, чтобы ответить на вопрос «на 3 больше, чем 8»? – Как вычислить число, которое меньше числа 10 на 6? Задание № 13 (с. 44). – Прочитайте первую задачу. – Что известно? Что необходимо узнать? – Используя фишки, решите эту задачу. 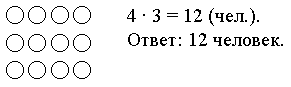 – Прочитайте вторую задачу. – Сравните эту задачу с первой. Чем они отличаются? – Что известно в задаче? Что требуется узнать? – Используя фишки, решите задачу. 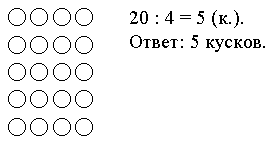 2. Работа в печатной тетради № 1. Задание № 59. Если учащиеся будут испытывать затруднения в выполнении этого задания, то учитель может подсказать, что, для того чтобы правильно подобрать знак в каждом конкретном случае, нужно сравнить первый компонент действия с результатом.
После выполнения этого задания учитель проводит устную проверку. Справочный материал для учителя История возникновения знаков плюс (+) и минус (–) – Вы когда-нибудь задумывались над тем, откуда в наших тетрадях и учебниках появились такие необходимые и в то же время простые знаки «+» и «–»? Оказывается, их история уходит в глубокую древность. Обычно виноторговец черточками отмечал, сколько мер вина он уже продал. Так, уменьшение количества стало обозначаться знаком «–», который позже назвали минусом. Приливая в бочку новые запасы, торговец перечеркивал столько расходных черточек, сколько мер он восстановил. Так, возможно, появился знак «+», обозначающий прибавление, увеличение. Иногда исторические факты со временем искажаются и не всегда бывают достоверными, поэтому многие ученые считают, что происхождение этих знаков имеет совсем другие корни. Давайте познакомимся и с другим мнением. Раньше, когда знаки плюс и минус не были известны древним математикам, сумму чисел записывали так: 1 и 2 или на латинском 1 et 2. Для краткости стали писать 1 t 2, а потом 1 + 2. VI. Итог урока. – Что нового узнали на уроке? – Какое действие необходимо выполнить, чтобы ответить на вопрос: «На сколько больше?» Домашнее задание: № 14 (учебник); № 58 (рабочая тетрадь). Урок 18 Сложение и вычитание вида 26 2, 26 10 Цели урока: продолжить формирование умений выполнять приемы сложения и вычитания двузначных чисел, основанные на поразрядном сложении и вычитании; совершенствовать навыки решения задач; развивать умение анализировать и обобщать. Ход урока I. Организационный момент. II. Устный счет. 1. Из каких фигур построен дом? 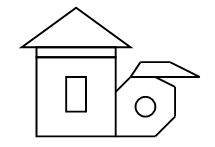 2. Прочитайте поговорку. 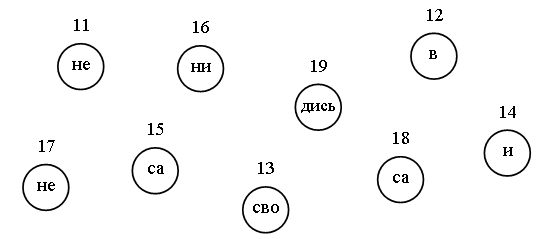 О т в е т: Не в свои сани не садись. 3. Расшифруйте слово.
4. Поставьте знаки действий «+» и «–» между числами так, чтобы получилось верное равенство. 5 … 4 … 3 … 2 … 1 = 1 О т в е т: 5 – 4 + 3 – 2 – 1 = 1. 5. Решите задачу. В коробке 3 желтых и 3 красных шарика. Мальчик взял 4 шарика. Сколько шариков каждого цвета может быть у мальчика? Найдите все ответы.
– Сколько шариков осталось в коробке? III. Сообщение темы урока. Работа над новым материалом. – Сегодня мы продолжим работу по сложению и вычитанию двузначных чисел. Задание № 4 (с. 41). – Рассмотрите данные выражения. Что их объединяет? (В каждом выражении по 2 арифметических действия и есть скобки.) – Какое действие надо выполнять первым? (В скобках.) – Какие правила сложения и вычитания двузначных чисел вы знаете? (Действия (сложение и вычитание) надо выполнять поразрядно.) Запись: 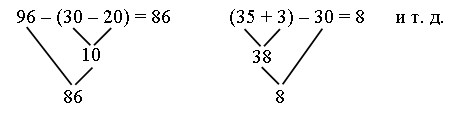 Задание № 5 (с. 42). Учащиеся, не выполняя вычислений, определяют, что больше: а) 46 + 2 больше 46 – 2, так как сложение двух чисел всегда больше разности этих же чисел; б) 53 + 4 меньше 6 + 53, так как в данных суммах, используя закон перестановки слагаемых, выясняем, что первое слагаемое одно и то же число – 53. Значит, значение суммы зависит от второго слагаемого: в первом выражении второе слагаемое меньше, чем второе слагаемое во втором выражении (4 < 6), поэтому значение первой суммы меньше значения второй суммы; в) 90 – 60 больше 80 – 60, так как вычитаемые равны, то значение разности больше в том выражении, где больше уменьшаемое (90 > 80); г) 37 – 5 больше 37 – 6, так как уменьшаемые равны, то значение разности больше в том выражении, где меньше вычитаемое (5 < 6). – Выполните сложение и вычитание данных чисел и проверьте свои рассуждения. Задание № 6 (с. 42). – Прочитайте текст. Можно ли его назвать задачей? – Прочитайте только условие. – Прочитайте вопрос задачи. – Сформулируйте вопрос задачи со словом «сколько». (Сколько килограммов весят яблоки в этом ящике?) – Запишите решение этой задачи. Всего: 23 кг. Ящик – 1 кг. Яблоки – ? кг. Решение: 23 – 1 = 22 (кг) – масса яблок. Ответ: 22 кг.  V. Повторение пройденного материала. 1. Работа по учебнику. Задание № 15 (с. 44). – Прочитайте задачу. – Что известно в задаче? Что требуется узнать? – Запишите кратко условие задачи. Запись: 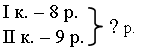 – Что обозначает слово «цена»? (Стоимость одного предмета.) – Что обозначает слово «стоимость»? (Выраженная в деньгах ценность чего-либо.) – Запишите решение этой задачи. (8 + 9 = 17.) – Измените вопрос задачи так, чтобы она решалась вычитанием. (На сколько рублей дороже второй карандаш?) Справочный материал для учителя Денежная система в Древней Руси Торговать люди умели с древнейших времен, но вот деньги появились не так давно. В Древней Руси, когда городами правили князья, появились необычные деньги: не монеты, а слитки из серебра и золота. Слиток из плохого серебра был самой мелкой монеткой и назывался гривна. Слиток из качественного серебра был более ценной деньгой, и называли его серебряный. Ну а золотой слиток ценился выше всех, его так и называли – золотой. Вы понимаете, что ходить за покупками с тяжелым слитком неудобно. Да к тому же, если товара нужно было немного, то, имея такой небольшой ассортимент денег, невозможно было дать сдачу покупателю. Тогда люди додумались делить гривну на несколько частей и стали рубить слитки. Так появился рубль, которым мы называем наши деньги и сейчас. Еще одна денежная единица, копейка, пришла к нам из древности: так назвали монету, на которой был изображен всадник с копьем. Отсюда и копейка. Были еще и другие монеты: деньга (полкопейки), алтын (3 копейки), пятак (5 копеек), гривенник (10 копеек), полтинник (50 копеек). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
