Физкультур минутка по математики. V. Повторение пройденного материала. Работа в печатной тетради Задание 23
 Скачать 2.68 Mb. Скачать 2.68 Mb.
|
|
VI. Путешествие в прошлое. Учащиеся читают текст на с. 71. – Перед тем как читать зашифрованное высказывание Галилея, надо найти ключ к шифру. А сделать это можно, разобравшись в таблице после текста. (Шифр: каждому многоугольнику определенной формы и цвета соответствует определенная буква.) Слова великого ученого: Язык природы есть язык математики. Справочный материал для учителя Галилео Галилей (1564–1642) Галилео Галилей – великий итальянский физик, математик, инженер и астроном, один из основателей современного естествознания. Еще подростком познакомился Галилей с трудами древнегреческих ученых – Аристотеля, Архимеда, Евклида – и в 20 лет, оставив медицину, которую изучал и Пизанском университете, погрузился в занятия физикой и астрономией. Галилей был профессором математики и физики в крупнейших итальянских университетах. Его научная деятельность и огромной важности открытия оказали решающее влияние на развитие механики, оптики, астрономии. Он создал раздел науки о движении – кинематику, законы которой вывел из точных экспериментов; сформулировал некоторые принципы классической механики; развил законы статики; заложил основы небесной механики. Открытия Галилея в астрономии буквально потрясли современников. Они стали первыми неопровержимыми доказательствами правильности гелиоцентрической теории Коперника, которую Галилей страстно защищал и пропагандировал, несмотря на жестокие гонения со стороны церкви. При наблюдении неба Галилей использовал совершенно новый инструмент – телескоп, который построил сам на основе только что изобретенной тогда (1609) в Голландии зрительной трубы. Увеличение своих телескопов Галилей довел от 3-кратного до 32-кратного. Галилей обнаружил фазы у Венеры и открыл четыре спутника Юпитера (их называют галилеевскими). Наблюдая Луну, Галилей обнаружил, что на ней есть горы, долины, глубокие пропасти, т. е. поверхность Луны по своему рельефу похожа на поверхность Земли. Телескоп Галилея впервые разложил на звезды некоторые туманные пятна на небе. Так, сплошное сияние Млечного Пути оказалось гигантским скоплением звезд. Вообще, при телескопических наблюдениях стало видно громадное количество звезд и впервые была постигнута их колоссальная удаленность. Галилею принадлежит открытие ярких пятен – флоккулов на Солнце, перемещение которых подтвердило незадолго до того обнаруженное вращение этого светила. Все наблюдения Галилей описал в небольшой работе «Звездный вестник». Убедившись в справедливости системы Коперника, Галилей посвятил ей свое основное астрономическое сочинение «Диалог о двух главнейших системах мира – птолемеевой и коперниковой» (1632). Оно было резко осуждено церковью (система Коперника с 1616 г. находилась под запретом). Престарелого ученого принудили к публичному покаянию, и последние годы жизни он провел под домашним арестом и надзором инквизиции. «Диалог» Галилея вошел и историю естествознания как символ гражданского мужества ученого и как яркая демонстрация торжества учения Коперника о Вселенной. VII. Итог урока. – Что нового узнали на уроке? – Как вычислить периметр треугольника? – Как вычислить длину стороны треугольника, если известны периметр и две другие стороны? Домашнее задание: № 12 (учебник); № 98 (рабочая тетрадь). Урок 35 Периметр многоугольника Цели урока: совершенствовать навыки решения задач на вычисление периметров любых многоугольников; продолжить формирование вычислительных навыков; закреплять навыки измерения длин сторон многоугольников и построение многоугольника с помощью линейки; развивать логическое мышление и внимание. Ход урока I. Организационный момент. II. Устный счет. 1. Сколько треугольников изображено на рисунке? 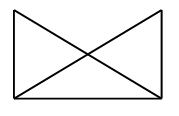 Ответ: 5. 2. Заполните фишки. 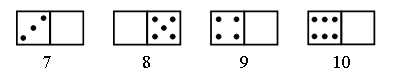 3. Решите задачу. Стоят 6 стаканов в ряд, первые 3 из них с водой. Как переставить 2 стакана так, чтобы пустой стакан и стакан с водой чередовались? 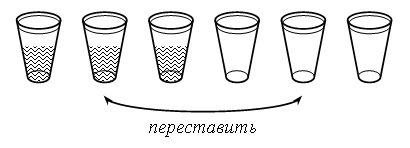 4. Рассмотрите чертежи. – Догадайтесь, по какому признаку можно разбить эти фигуры на группы.    III. Сообщение темы урока. – Сегодня мы продолжим закреплять навыки вычислений периметра многоугольника. IV. Работа по теме урока. 1. Работа по учебнику. Задание № 6 (с. 68). – Рассмотрите чертеж. Какие фигуры здесь изображены? – Что такое многоугольник? – Как определить название каждого многоугольника? (Посчитать количество углов, вершин или сторон.) – Как называются данные многоугольники? – Что такое периметр многоугольника? – Что надо знать, чтобы вычислить периметр? – Выполните необходимые измерения и вычислите периметр многоугольников. 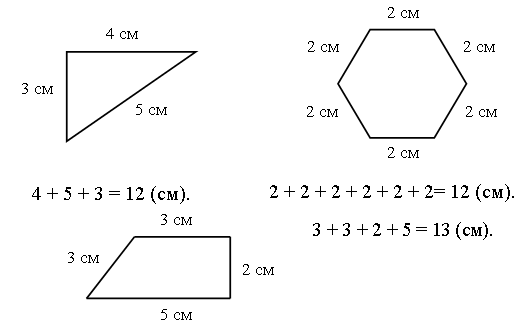 Задание № 14 (с. 70). – Прочитайте задачу. – Что известно в задаче? – Что требуется узнать? Учащиеся выполняют схему к данной задаче. 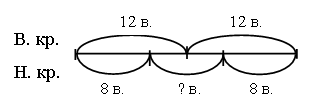 Решение: I способ. 1) Сколько ведер воды наливается за 2 часа через верхний кран? 12 + 12 = 24 (в.). 2) Сколько ведер воды выливается за 2 часа через нижний кран? 8 + 8 = 16 (в.). 3) Сколько ведер воды останется в баке? 24 – 16 = 8 (в.). II способ. 1) 12 – 8 = 4 (в.) – воды остается в баке за час. 2) 4 + 4 = 8 (в.) – воды остается в баке за 2 часа. Ответ: 8 ведер. Задание № 16 (с. 70). Учащиеся восстанавливают примеры: 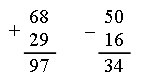 2. Работа в печатной тетради № 1. Задание № 102. При выполнении задания лучше всего искать не каждую отдельную цифру числа, а все неизвестное число. Рассмотрим случай: 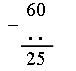 Изобразим «машину»: 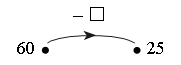 В «машину» ввели число 60, «машина» вычла из него какое-то число. Вышло число 25. Сколько вычла «машина»? Из «машины» вышло число, меньшее 60. На сколько? На столько, сколько вычла «машина». Как это узнать? Нужно из большего числа (60) вычесть меньшее (25): 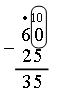 Значит, неизвестное число – 35. Далее выполняем проверку. Если нет калькулятора, проверку можно сделать так: 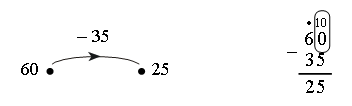 Аналогично можно рассуждать в остальных случаях. Задание № 104. Задание является подготовительным к теме «Взаимное расположение фигур на плоскости». Воспользовавшись линейкой, учащиеся убеждаются, что луч пересекает стороны пятиугольника в двух точках – А и В. 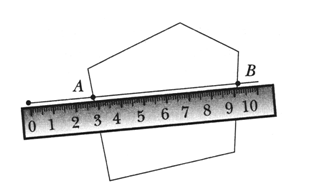  V. Самостоятельная работа по карточкам. Найдите периметр каждой фигуры. 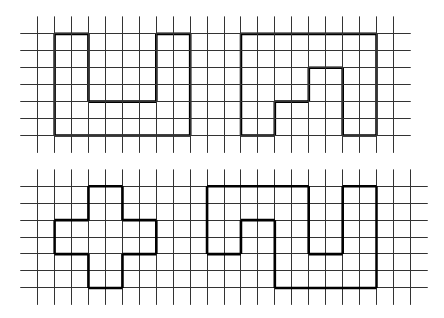 VI. Итог урока. – Что нового узнали на уроке? Домашнее задание: № 105 (рабочая тетрадь). Урок 36 Окружность, ее центр и радиус Цели урока: познакомить учащихся с понятием «окружность»; ввести термины «центр окружности», «радиус окружности»; рассмотреть построение окружности с помощью циркуля; совершенствовать вычислительные навыки; развивать логическое мышление и внимание. Ход урока I. Организационный момент. II. Устный счет. 1. Рассмотрите фигуры. Определите, чем каждая следующая отличается от предыдущей. Нарисуйте четвертую фигуру, не нарушая закономерности. 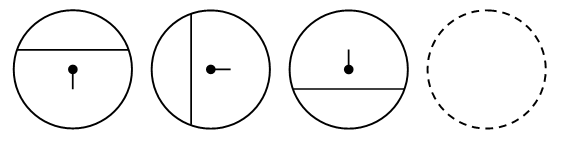 2. В каждой из трех ваз стояли цветы: или колокольчики, или васильки, или ромашки. В первой вазе не было ромашек, во второй не было ни ромашек, ни васильков. Какие цветы стояли в каждой вазе? 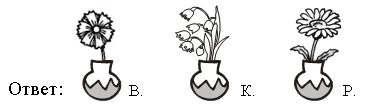 3. Расшифруйте слово.
4. Сколько четырехугольников на чертеже? 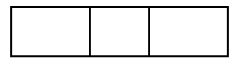 Ответ: 6. III. Сообщение темы урока. – Рассмотрите фигуры, данные на доске: 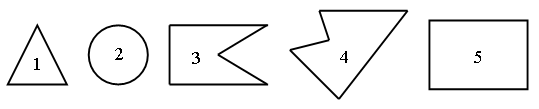 – Найдите «лишнюю» фигуру. (Номер 2.) – Как она называется? – Сегодня на уроке мы познакомимся с новым понятием «окружность». IV. Изучение нового материала. Несмотря на то что определение окружности учащимся не дается, необходимо познакомить их со свойством точек окружности. Подготовительное упражнение. Учитель отмечает на доске какую-нибудь точку и обозначает ее буквой О (учащиеся выполняют то же самое в своих тетрадях). Далее учитель отмечает сначала одну, затем другую, третью, четвертую точки, каждая из которых находится на расстоянии 2 см от точки О. При этом можно использовать линейку или циркуль. В результате получится такой чертеж: 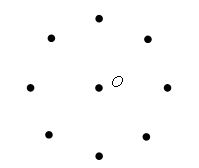 – Можно отметить еще очень много точек, каждая из которых находится на расстоянии 2 см от точки О. Давайте представим себе, что нам удалось отметить все такие точки. Все точки, находящиеся на расстоянии 2 см от точки О, образуют фигуру, которую называют словом «окружность». Чтобы изобразить окружность, не нужно отмечать все точки, для этого нам понадобится циркуль. Посмотрите, как нужно правильно им пользоваться. Отмечаем точку О; она будет центром окружности. Берем циркуль и немного разводим в стороны концы его ножек (не обязательно на 2 см, можно взять любое расстояние). Держа циркуль правой рукой (покажите), ставим в точку О ножку циркуля с иглой. Чуть отклоняя циркуль, поворачиваем ножку с карандашом вокруг точки О, касаясь карандашом доски. Получается окружность. Теперь вы сами попробуйте начертить окружность в тетрадях. Отмечайте центр окружности. Далее берите циркуль. Проводя окружность, придерживайте тетрадь левой рукой. Окружность чертить трудно, поэтому придется потренироваться. Изобразите несколько окружностей. – Рассмотрите чертеж на доске. – На какие две группы можно разделить фигуры на рисунке? 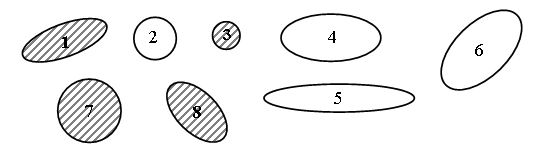 – Запишите номера и общее название фигур каждой группы. I группа – это линии (2, 4, 5, 6); II группа – это фигуры (1, 3, 7, 8). – Разделите эти же фигуры на 2 группы по другому признаку. Запишите номера фигур новых групп и объясните, в чем сходство фигур каждой группы. I группа – это линии, которые являются границей круга, т. е. окружности (2). II группа – это линии, которые являются границей овала (4, 5, 6). III группа – фигуры, которые являются кругами (3, 7). IV группа – фигуры, которые являются овалами (1, 8). – Рассмотрите рисунок. Что здесь изображено? (Рис. а – круг, рис. б – окружность.) 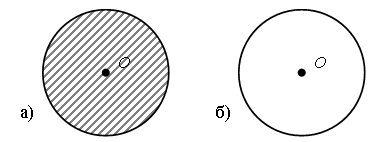 – Каким инструментом удобно чертить окружность? – Как называется точка О? (Центр окружности.) – Отметьте любую точку на окружности. Соедините отрезком центр окружности с этой точкой. Этот отрезок называют радиусом.
– Постройте еще несколько радиусов этой окружности. – Назовите радиусы на чертеже. (ОА, ОВ, ОС, OD, ОЕ.) 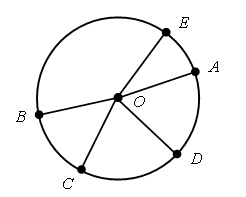 – Сколько радиусов можно провести в одной и той же окружности? – Измерьте длину каждого радиуса. Почему все радиусы окружности имеют одну и ту же длину? Задание № 1 (с. 72). – Какие предметы похожи на окружность? (Обруч, колесо, солнце и т. д.) – Рассмотрите чертеж (с. 72 учебника). – Покажите концом указки окружность (конец указки должен скользить по окружности). – Покажите центр окружности. (Это точка.) – Покажите радиус окружности. (Это отрезок.) – Рассмотрите правую часть чертежа. Что здесь изображено? (Способ построения окружности с длиной радиуса 4 см.) – Расскажите о порядке работы. – Выполните данное построение окружности на доске и в тетрадях. Задание № 2 (с. 72). Используя циркуль, учащиеся строят в тетради три разные окружности. – Отметьте центр каждой окружности. – Укажите длину радиуса. 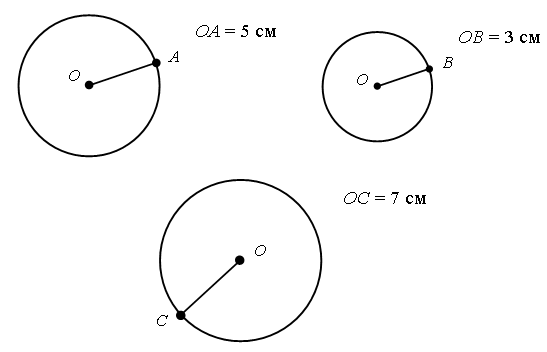 Задание № 3 (с. 72). Перед выполнением задания необходимо обсудить с учащимися план построения окружности. 1. Отметить произвольную точку О – центр окружности. 2. Установить расстояние между ножками циркуля, равное 5 см, то есть длине радиуса окружности. 3. Выполнить построение окружности. Задание № 4 (с. 72). Учащиеся строят окружность и проводят в ней три радиуса. – Сколько еще радиусов можно провести для этой окружности? |
