Физкультур минутка по математики. V. Повторение пройденного материала. Работа в печатной тетради Задание 23
 Скачать 2.68 Mb. Скачать 2.68 Mb.
|
|
Задание № 16 (с. 60). Последовательность чисел составлена по принципу: из первого числа вычитается 5, а затем к полученному числу прибавляется 10. И так далее:
Следующее число: 25 – 5 = 20. Задание № 17 (с. 60). – Рассмотрите данные на рисунке фигуры. Как их можно назвать? (Это все многоугольники.) – Какие фигуры называют многоугольниками? – Как определить название многоугольника? (По количеству в нем углов, вершин, сторон.) – Какие многоугольники называют четырехугольниками? – Назовите номера всех четырехугольников. (1, 3, 4.) – Какой четырехугольник является «лишним»? (3, так как это невыпуклый четырехугольник.) – Назовите признаки выпуклых многоугольников. Задание № 18 (с. 60). – Рассмотрите данные фигуры. – Что их объединяет? (Это многоугольники.) – На какие две группы можно разбить данные многоугольники? Укажите признак каждой группы. I группа (1, 2) – выпуклые многоугольники; II группа (3, 4) – невыпуклые многоугольники. – Какие из данных фигур являются пятиугольниками? (3.) 2. Работа в печатной тетради № 1. Задание № 87. Рассмотрим, как должны рассуждать учащиеся. Сумма единиц складываемых чисел равна 9. Так как во втором числе 7 единиц, то в первом их должно быть: 9 – 7 = 2. Сумма десятковтоже равна 9. 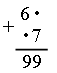 Так как в первом числе 6 десятков, то во втором их должно быть: 9 – 6 = 3. Подставляем вместо точек найденные цифры. Далее устно выполняется проверка. 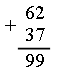 Задание № 88. Учащиеся выбирают правильный ответ – «нет». Далее учитель проводит дополнительную работу с текстом задачи. – Кого больше в стаде: коров или быков? (Коров.) – А как узнать, на сколько больше коров? Выполните вычисления устно. (Из 24 вычесть 3, получится 21.) – А на сколько меньше быков, чем коров? (На 21.) – Можно ли узнать, сколько всего коров и быков в стаде? Как это сделать? (24 + 3 = 27.) – Пусть в стаде 2 теленка. Можно ли теперь ответить на вопрос задачи? – Как проще всего решить задачу? (27 + 2 = 29.) VI. Итог урока. – Что нового узнали на уроке? – Какую фигуру называют многоугольником? – Как определить название многоугольника? Домашнее задание: № 13, 14 (учебник); № 86 (рабочая тетрадь). Урок 29 Сложение двузначных чисел (общий случай) Цели урока: закреплять знания учащихся о симметричных фигурах, о многоугольниках; совершенствовать частные и общие приемы сложения двузначных чисел; рассмотреть способы преобразования задач; развивать внимание и память. Ход урока I. Организационный момент. II. Устный счет. 1. Задачи. – Сравните тексты задач.
– Чем они похожи? – Чем они отличаются? – Как можно дополнить условие каждой задачи, чтобы ответить на поставленный вопрос? 2. Маша и Катя стреляли из лука. Кто из них оказался победителем после трех попыток? 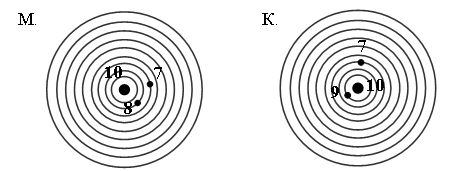 Кто набрал очков больше и на сколько? 3. Чему равна масса арбуза? Чему равна масса дыни? 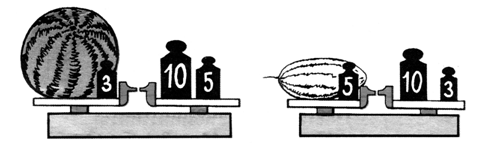 4. Найдите признак, по которому данные фигуры можно разбить на две группы. 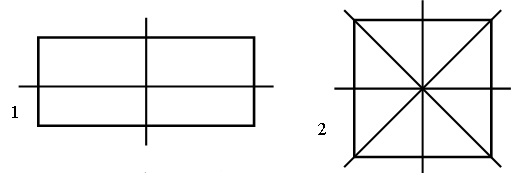 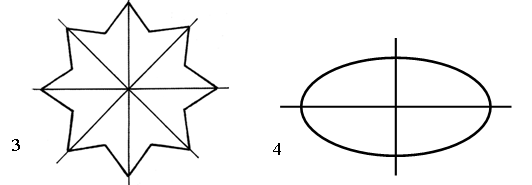 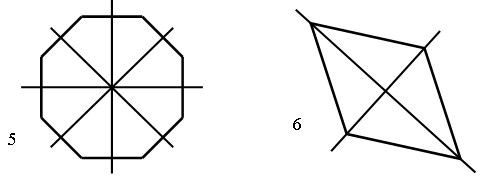 I группа (1, 4, 6) – фигуры, которые имеют две оси симметрии; II группа (2, 3, 5) – фигуры, которые имеют более двух осей симметрии. – Что такое ось симметрии? – Какие фигуры называют симметричными? III. Сообщение темы урока. – Сегодня мы продолжим закреплять навыки двузначных чисел. IV. Работа по теме урока. 1. Работа по учебнику. Задание № 6 (с. 57). – Прочитайте текст. Можно ли его назвать задачей? Почему? – Что известно в задаче? – Что требуется узнать? – Запишите кратко условие задачи и решите ее. Запись: Было – ? кн. Взяли – 8 кн. Осталось – 12 кн. Решение: 12 + 8 = 20 (кн.) – было. О т в е т: 20 книг. – Измените вопрос задачи так, чтобы она решалась вычитанием. («На сколько больше книг осталось на полке, чем взяли?» 12 – 8 = 4 (кн.).) Задание № 7 (с. 57). – Прочитайте условие задачи. – Что известно? Что требуется узнать? – Запишите кратко условие задачи и решите ее разными способами. Запись: Было – 15 в. и 28 в. Отцепили – 3 в. Стало – ? в. Решение:
Задание № 19 (с. 61). – Рассмотрите чертеж. Что на нем изображено? – Что называют числовым лучом? – Прочитайте задание к чертежу. Учащиеся должны рассуждать примерно так: «Координата точки А – число 15, значит, эта точка расположена на расстоянии 15 единиц от начала числового луча. Координата точки В – число 9, значит, эта точка расположена на расстоянии 9 единиц от начала числового луча. Найдем, на сколько единиц дальше от начала числового луча находится точка А, чем точка В: 15 – 9 = 6. Ответ: на 6 единиц». Задание № 21 (с. 61). – Прочитайте задание и выполните схематичный рисунок.  2. Работа в печатной тетради № 1. Задание № 90. Учащиеся проводят ось симметрии в каждой фигуре. 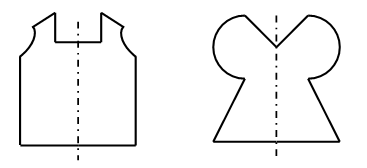  V. Самостоятельная работа. I вариант. № 1. Запишите числа с помощью цифр.
№ 2. Решите примеры.
№ 3. Решите задачу. Миша и Маша собрали 86 кг яблок. Миша собрал 51 кг яблок. Сколько килограммов яблок собрала Маша? № 4. Укажите номера пятиугольников.  II вариант. № 1. Запишите числа с помощью цифр.
№ 2. Решите примеры.
№ 3. Решите задачу. С двух участков собрали 74 ведра картофеля. С одного участка собрали 43 ведра картофеля. Сколько ведер картофеля собрали с другого участка? № 4. Укажите номера четырехугольников.  VI. Итог урока. – Что нового узнали на уроке? – Какие фигуры называют симметричными? – Что такое числовой луч? Домашнее задание: № 20, 22 (учебник); № 89 (рабочая тетрадь). Урок 30 Вычитание двузначных чисел (общий случай) Цели урока: рассмотреть вычитание двузначных чисел с переходом в другой разряд; совершенствовать вычислительные навыки; продолжить формирование умений составлять и преобразовывать задачи; вести подготовительную работу к изучению уравнений; развивать умение анализировать и рассуждать. Ход урока I. Организационный момент. II. Устный счет. Вставьте в «окошки» однозначные числа, чтобы получились верные равенства:
2. Покажите отрезками рост каждой девочки, если Ира и Лена одинакового роста, Лена выше Оли, а Таня выше Иры. Напишите, кто выше всех: Таня или Оля. _____________ Таня Ира Лена Оля  3. Рассмотрите рисунок. Не нарушая закономерности, дорисуйте недостающий флажок. 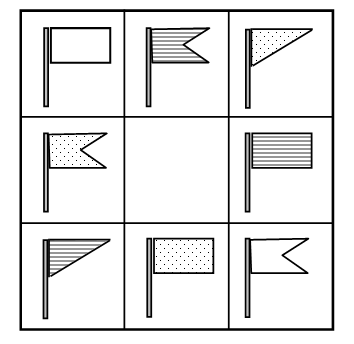 4. Рассмотрите внимательно рисунки. Чем они похожи? Чем отличаются? Подберите к рисункам числовые выражения и объясните, что обозначает каждое число в этих выражениях. 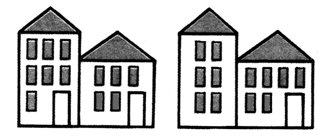 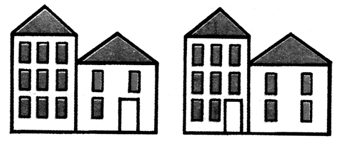 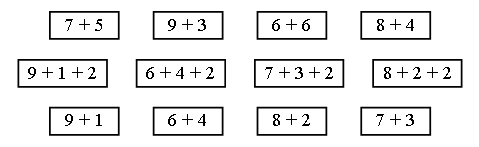 – Чем похожи выражения верхнего и среднего ряда? Чем похожи выражения нижнего ряда? – Найдите значение каждого выражения. III. Сообщение темы урока. – Рассмотрите математические записи на доске:
– Чем отличаются выражения каждого столбика? – Сегодня на уроке мы рассмотрим прием поразрядного вычитания в случае, когда в разряде единиц уменьшаемого их меньше, чем в разряде единиц вычитаемого. IV. Изучение нового материала. Перед рассмотрением общего случая вычитания двузначных чисел учитель предлагает подготовительные упражнения: 1. Назовите разность: 12 и 5 11 и 4 17 и 8 13 и 7 10 и 8 12 и 6 2. Назовите число на 1 меньше, чем каждое из чисел: 8, 4, 9, 6, 5, 1, 3, 2, 7. 3. Число 5 можно записать так: Какое число означает каждая из записей: Задание № 1 (с. 62). – Рассмотрите рисунок и объясните, как выполняли вычитание 52 – 37 Волк и Заяц, используя цветные палочки. Итак, действуем, как раньше. Составим «поезд» из 5 оранжевых и 2 белых «вагонов»:
От него нужно отцепить 3 оранжевых и 7 белых «вагонов». Но у нас всего 2 белых «вагона». Поэтому возьмем один оранжевый «вагон» (лучше примыкающий к белым) и заменим его 10 белыми «вагонами». Теперь у нас получился поезд, состоящий из 4 оранжевых и 12 белых «вагонов»: число 52 будет выглядеть так:  От 12 белых «вагонов» отцепляем 7, остается 5 белых «вагонов», а от 4 оранжевых отцепляем 3:  Остается «поезд», состоящий из 1 оранжевого «вагона» и 5 белых «вагонов». Он обозначает число 15. 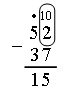 Данная форма записи особенно эффективна на первоначальном этапе освоения детьми алгоритма вычитания. Когда второклассники приобретут необходимые навыки вычитания, можно будет перейти к общепринятой записи. На с. 62 учебника приведены примеры на вычитание, записанные столбиком. Рассмотрите их со всем классом подробно, не торопясь, с необходимыми комментариями, привлекая учащихся к объяснению шагов алгоритма. Приведем образцы рассуждений. Пример 1. 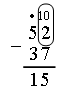 О б ъ я с н е н и е: 2 меньше 7. Из 5 десятков возьмем 1 десяток (ставим над 5 точку). В десятке – 10 единиц (запишем 10 над 2). 12 без 7 – это 5 (пишем 5 под 7), 4 без 3 – это 1 (пишем 1 под 3). Разность – 15. Пример 2. 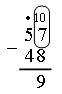 О б ъ я с н е н и е: 7 меньше 8. Берем 1 десяток. 17 без 8 – это 9, 4 без 4 – это 0. Впереди 9 единиц нуль не пишем. Разность – 9. Пример 3. 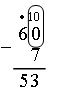 О б ъ я с н е н и е: 0 меньше 7. Берем 1 десяток. 10 без 7 – это 3, 5 без 0 – это 5. Разность – 53. Задание № 2 (с. 63). Учащиеся выполняют вычитание столбиком на доске, комментируя каждое действие. |
