Физкультур минутка по математики. V. Повторение пройденного материала. Работа в печатной тетради Задание 23
 Скачать 2.68 Mb. Скачать 2.68 Mb.
|
|
Справочный материал для учителя В математике окружность определяют по-разному. С теоретико-множественной точки зрения окружность – это множество точек, находящихся на одном и том же расстоянии от одной точки, называемой центром окружности. При этом центр окружности самой окружности не принадлежит. Определение. Окружностьюназывается фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки. Эта точка называется центром окружности. Расстояние от точек окружности до ее центра называется радиусом окружности. Радиусом называется также любой отрезок, соединяющий точку окружности с ее центром (рис. 1). 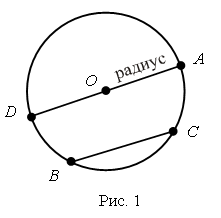 Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр, называется диаметром. На рисунке 1 ВС – хорда, AD – диаметр.  V. Повторение пройденного материала. 1. Работа по учебнику. Задание № 9 (с. 73). – Рассмотрите математические записи. Чем они похожи? (Есть скобки.) – Каков порядок выполнения арифметических действий в выражениях со скобками? – Вычислите их значение. Запись: (80 – 7) + 13 = 86 52 – (6 + 18) = 28 и т. д. 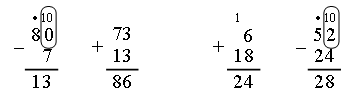 Задание № 11 (с. 74). – Какую фигуру называют треугольником? – Что известно в задаче? – Что требуется узнать? – Как вычислить периметр многоугольника? Запись: 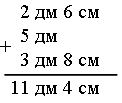 Ответ: 11 дм 4 см. 2. Работа в печатной тетради № 1. Задание № 116. – Рассмотрите рисунок. Что здесь изображено? – Составьте по данному рисунку задачу. Задание можно использовать для тренировки в записи решения задачи выражением. При этом слабым детям можно предложить в помощь следующую карточку: 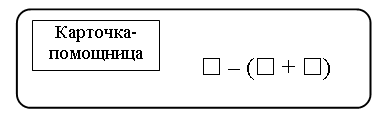 3. Самостоятельная (практическая) работа по теме: Карточка'>Окружность Карточка А Проведите окружность с центром в точке О так, чтобы она проходила: а) через точку А, и закрасьте круг радиусом ОА; 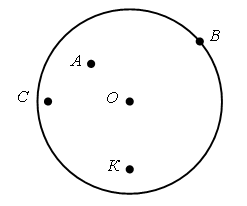 б) через точку К, и закрасьте круг радиусом ОК; 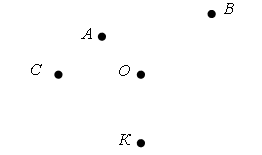 в) через точку С, и закрасьте круг радиусом ОС. 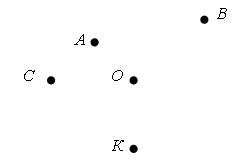 Карточка В Отметьте красным цветом точки, которые находятся на окружности с центром в точке О. 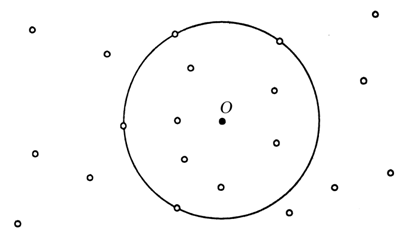 Карточка С Отметьте синим цветом точки пересечения: а) двух окружностей; 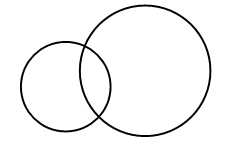 б) окружности и прямой; 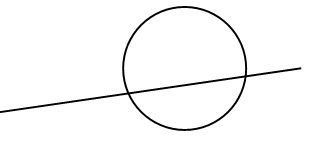 в) окружности и ломаной; 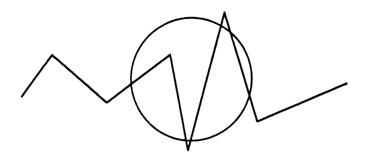 г) окружности и кривой. 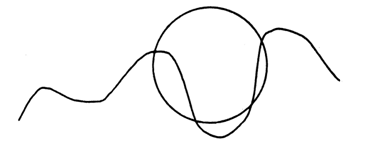 Карточка D Проведите окружность, радиус которой:
 VI. Итог урока. – Что нового узнали на уроке? – Что такое окружность? – Что называют центром окружности? – Что такое радиус окружности? – Как вычислить периметр многоугольника? Домашнее задание: № 10 (учебник); № 111, 112, 115 (рабочая тетрадь). (Задание 112 имеет практическую направленность. Учащиеся учатся заполнять бланк почтового перевода.) Урок 37 Окружность, ее центр и радиус. окружность и круг Цели урока: рассмотреть и сравнить признаки окружности и круга; продолжить формирование умений измерять длину радиуса окружности, строить окружность с помощью циркуля; совершенствовать навыки решения задач; развивать внимание и пространственное мышление. Ход урока I. Организационный момент. II. Устный счет. 1. Рассмотрите фигуры. Определите, чем каждая следующая отличается от предыдущей. Нарисуйте четвертую фигуру, не нарушая закономерности.  2. Решите задачу. На велогонках стартовали 70 спортсменов. На первом этапе с трассы сошли 4 велосипедиста, на втором – 6. – Сколько спортсменов пришло к финишу? – Выберите выражение, которое является решением задачи:
3. Вставьте знаки арифметических действий, чтобы получились верные равенства:
4. Анализ чертежа. – На какие две группы можно разделить фигуры на рисунке? 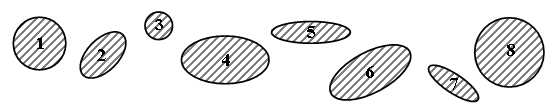 – Запишите номера и общее название фигур каждой группы. – Сравните свои группы с такими: I группа – фигуры 1, 3, 8; II группа – фигуры 2, 4, 5, 6, 7. – Они похожи? По какому признаку выделены эти группы? III. Сообщение темы урока. – Рассмотрите данный на доске чертеж: 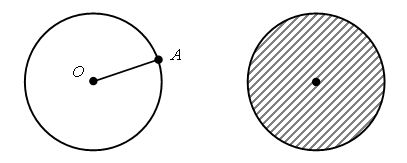 – Чем похожи и чем отличаются рисунки слева и справа? – Сегодня на уроке мы узнаем, чем отличается окружность от круга. IV. Изучение нового материала. Задание № 6 (с. 78). – Рассмотрите рисунок в учебнике. – Назовите, что имеет в очках форму окружности, а что – круга. (Стекло – это круг, а оправа – окружность.)
– В этом и состоит различие между кругом и окружностью. – Начертите в тетради какой-нибудь круг. В отличие от окружности круг нужно закрасить. – Отметьте центр этого круга и радиус. Задание № 7 (с. 73). Две разные окружности могут иметь один и тот же радиус лишь в том случае, если их центры – различные точки. (После устного обсуждения задания попросите учащихся в тетрадях построить две разные окружности с одним и тем же радиусом.) Задание № 8 (с. 73). Задание направлено на развитие внимания учащихся. На первом чертеже изображено 6 окружностей, на втором чертеже – 10 окружностей. Задание № 5 (с. 73). Чертеж: 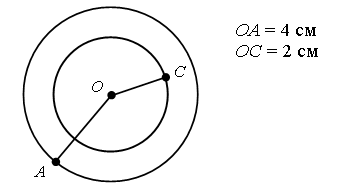  V. Повторение пройденного материала. 1. Работа в печатной тетради № 1. Задание № 106. Среди данных фигур только фигура № 3 является окружностью. По ходу выполнения задания обратите внимание учащихся на фигуру № 1 (круг). Попросите детей сравнить круг и окружность. Выясните, чем они похожи и чем отличаются. Задание № 107. Учащиеся объясняют, что при построении радиуса надо сначала выбрать произвольную точку на окружности. Соединив центр окружности и выбранную точку отрезком, мы получим радиус. Затем можно переходить к измерению длины радиуса (длины построенного отрезка). Она равна 2 см. Задание № 108. Так как в условии не указана длина радиуса, то ее мы можем выбрать произвольно. Значит, окружностей с центром в точке Р можно построить сколько угодно. Чертеж: 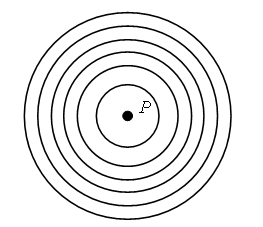 – Сколько окружностей у вас получилось? Задание № 110. Если у слабоуспевающих учащихся возникнут трудности при построении окружности, предложите им воспользоваться карточкой-помощницей. 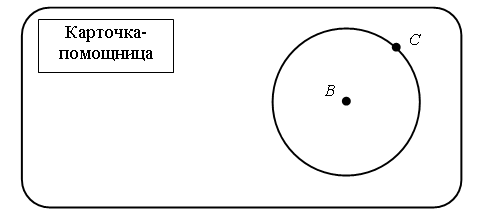 Учитель должен обратить внимание учащихся на то, что для измерения длины радиуса построенной окружности необязательно его строить. Достаточно измерить расстояние между точками В и С. Исходя из условия задания, можно построить единственную окружность, так как задан не только центр (В), но и радиус (ВС). 2. Работа по учебнику. Задание № 15 (с. 75). – Прочитайте текст. Является ли он задачей? – Что известно в задаче? – Что требуется узнать? При решении этой задачи учащиеся могут рассуждать следующим образом: «На каждой полке 15 книг, следовательно, на двух полках вместе: 15 + 15 = 30 (книг). Всего с двух полок сняли столько книг, сколько было на первой полке, то есть 15 книг, следовательно, на полках осталось: 30 – 15 = 15 (книг)». VI. Итог урока. – Что нового узнали на уроке? – Чем отличаются окружность и круг? Справочный материал для учителя Кругом называется фигура, состоящая из всех точек плоскости, расстояние от которых до данной точки не больше данного. Эта точка называется центром круга, а данное расстояние – радиусом круга. Границей круга является окружность с теми же центром и радиусом. Домашнее задание: № 13 (учебник); № 109 (рабочая тетрадь). Урок 38 Окружность, ее центр и радиус. Окружность и круг Цели урока: продолжить формирование умений строить окружности с помощью циркуля; совершенствовать навыки решения задач с величинами «цена», «количество», «стоимость»; вести подготовительную работу по выделению среди четырехугольников группы прямоугольников; развивать логическое мышление и умение обобщать. Ход урока I. Организационный момент. II. Устный счет. 1. Рассмотрите фигуры. Определите, чем каждая следующая отличается от предыдущей. Нарисуйте четвертую фигуру, не нарушая закономерности. 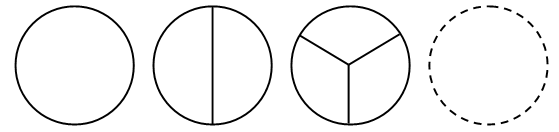 2. Решите задачу. Витя и Дима играют в бадминтон. Первая партия закончилась со счетом 11 : 5 в пользу Вити. Вторая партия – со счетом 11 : 7 в пользу Димы. а) Кто набрал очков больше? б) На сколько у одного мальчика очков больше, чем у другого? – Подумайте, на какой из этих вопросов можно ответить, не выполняя арифметического действия. 3. Вставьте знаки арифметических действий, чтобы получились верные равенства.
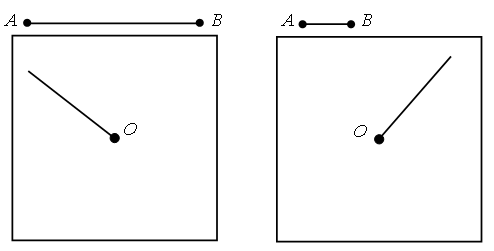
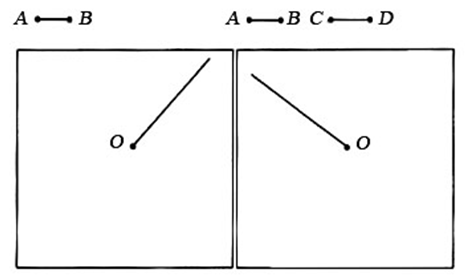
III. Сообщение темы урока. – Рассмотрите рисунки на доске. – Чем похожи и чем отличаются рисунки слева и справа? 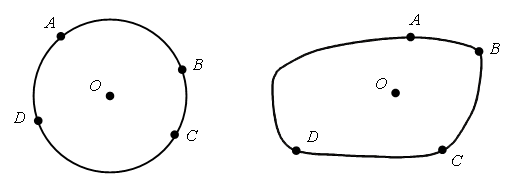 Учащиеся. Слева и справа нарисованы замкнутые кривые линии. На каждой из них отмечены 4 точки. Точка О находится внутри замкнутой линии на левом и на правом рисунках. – Вы назвали признаки, по которым рисунки похожи. А чем они отличаются? Учащиеся. На левом рисунке все точки, которые отмечены на замкнутой кривой, находятся на одинаковом расстоянии от точки О, а на правом рисунке это условие не выполняется. – Поставьте на одной и на другой линии слева еще 4 любые точки. На каком расстоянии от точки О они будут находиться? Замкнутая кривая слева – окружность. Точка О – центр окружности. – С помощью какого инструмента можно провести окружность? – Сегодня на уроке будем закреплять умение строить окружности. IV. Работа по теме урока. 1. Работа по учебнику. Задание № 12 (с. 74). – Рассмотрите чертеж. Что здесь изображено? (Многоугольник, четырехугольник, прямоугольник, квадрат.) – Назовите более точное название этой фигуры. (Квадрат.) – Укажите свойства квадрата. – Сравните с помощью циркуля длины сторон квадрата. Какой вывод можно сделать?
– Сколько измерений надо выполнить, чтобы найти периметр квадрата? (Одно измерение.) – Как вычислить периметр многоугольника? – Найдите периметр квадрата.  Задание № 14 (с. 74). – Рассмотрите рисунок. Что вы узнали? – Прочитайте текст задания. Что требуется узнать? – Запишите условие задачи в таблицу.
Было – 50 рублей. Решение: 1. Сколько стоят 2 плитки шоколада? 18 + 18 = 36 (р.). 2. Сколько стоят пачка печенья и шоколадка? 12 + 18 = 30 (р.). 3. Сколько стоят пачка вафель, пачка печенья и плитка шоколада? 10 + 12 + 18 = 40 (р.). 4. Сколько стоят 3 пачки печенья? 12 + 12 + 12 = 36 (р.). 5. Сколько стоят 2 пачки вафель, шоколадка и пачка печенья? 10 + 10 + 18 + 12 = 50 (р.). Задание № 16 (с. 75). – Прочитайте задание. Выполните рисунок к условию. 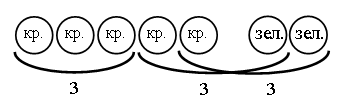 – Остался ли в коробке хотя бы один красный шар? (Да.) – Мог ли остаться в коробке хотя бы один зеленый шар? (Мог остаться, если бы взяли все красные шары или два красных и один зеленый.)  V. Самостоятельная работа по теме «Окружность, ее центр и радиус». Задание № 1. – Выберите рисунок, на котором все точки линии находятся на одинаковом расстоянии от точки О. – Как называется такая линия? 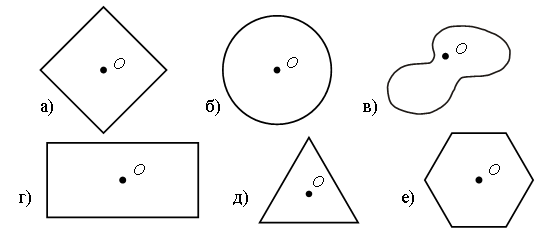 Задание № 2. – Рассмотрите рисунки. 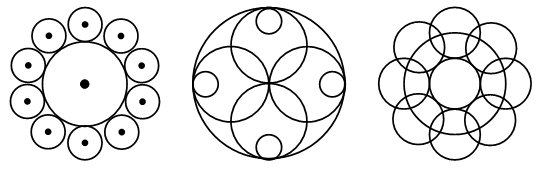 – Как получили такие красивые узоры? – Попробуйте начертить такие же узоры. – Придумайте свои узоры из окружностей. Задание № 3. – Измерьте длину радиусов каждой окружности: 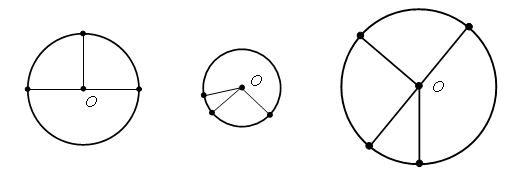 – Что о них можно сказать? (Радиусы одной окружности равны между собой.) – Начертите несколько своих окружностей и проведите в каждой несколько радиусов. Радиусы каждой из них равны? – Вы согласны, что все точки окружности находятся на одинаковом расстоянии от ее центра? Объясните свой ответ. Задание № 4. Можно ли провести окружность с центром в точке О так, чтобы она проходила через точки А, В, С, D? 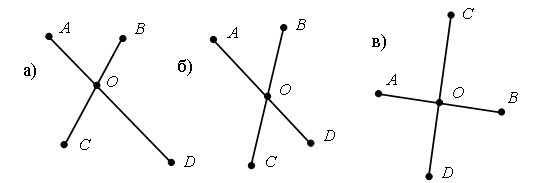 Задание № 5. Какие точки лежат на окружностях: а) с центром в точке О и с центром в точке М? б) с центром в точке М и с центром в точке К? 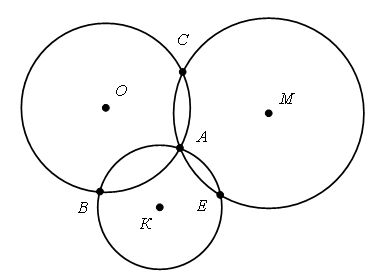 VI. Итог урока. – Рассмотрите рисунок 1 на доске. 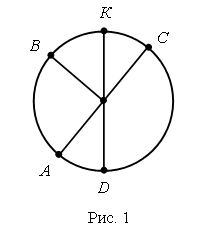 – Что на нем изображено? – Как называется отрезок ОА? – Подумайте, есть ли на рисунке другие радиусы этой окружности? – Назовите их. (ОВ, OD, OC, OK.) – Что же такое радиус? (Радиус – это отрезок, который соединяет центр окружности с точкой окружности.) – Рассмотрите второй рисунок на доске. 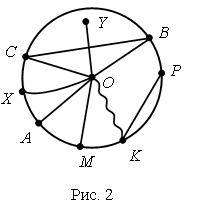 – Назовите имена линий, которые не являются радиусами. (СВ, OY, OX, OК, РК.) – Начертите окружность с радиусом 4 см. Проведите в ней красным цветом 3 радиуса, синим столько же отрезков, которые не являются радиусами. Домашнее задание: № 113 (рабочая тетрадь). |
