Физкультур минутка по математики. V. Повторение пройденного материала. Работа в печатной тетради Задание 23
 Скачать 2.68 Mb. Скачать 2.68 Mb.
|
|
IV. Изучение нового материала. Метр – это более крупная, чем сантиметр и даже дециметр, единица длины. В метрах измеряют, например, длину куска ткани или обоев, длину и ширину комнаты. При этом, например, для измерения длины комнаты используют рулетку – длинную ленту, свернутую в рулон, на которую нанесена шкала. Рулетки бывают разной длины – метровые, двухметровые, трехметровые, пятиметровые, двадцатиметровые и другие. – Назовите известные вам единицы измерения длины в порядке их увеличения. – Как обозначаются сантиметр и дециметр? (См и дм, при этом обозначения записываются без точек в конце.) – Метр обозначается буквой м (без точки). – Прочитайте записи на доске: 4 м, 45 м, 4 м 8 дм, 42 м 8 дм 9 см. – Рассмотрите рисунок в учебнике (с. 30). Какие инструменты для измерения длины здесь изображены? (Ученическая линейка, классная метровая линейка, рулетка.) – Что вы будете измерять каждым инструментом? – Прочитайте вслух текст на с. 30. Задание № 1 (с. 31). Используя классную метровую линейку, учащиеся заполняют пропуски в таблице соотношений между единицами длины.
Задание № 2 (с. 31). Учащиеся вслух читают записи. Задание № 3 (с. 31). Необходимо закончить фразы, вставив пропущенные единицы длины. Учащиеся работают самостоятельно. Затем учитель организует проверку. Высота дерева 2 м. Спортсмены пробежали дистанцию 100 м. Длина спички 4 см. Школьники приняли участие в заплыве на 50 м. Задание способствует формированию у учащихся реальных представлений о единицах длины. Поэтому учащиеся не только должны закончить предложение, но и объяснить, почему они выбрали именно эту единицу длины и можно ли ее заменить на какую-нибудь другую. Задание № 4 (с. 31). Под руководством учителя дети измеряют свой рост, длину своего шага и записывают в тетрадь результаты измерений.  V. Повторение пройденного материала. 1. Работа в печатной тетради № 1. Задание № 42. Так как учащиеся еще незнакомы с символами «>» и «<», то оформить решение они должны так: Запись: 10 см меньше 1 м; 49 дм меньше 5 м; 80 см больше 7 дм; 5 дм меньше 60 см. Задание № 43. Длина ручки см. Это дм см. 2. Работа по учебнику. Задание № 10 (с. 32). Учитель проводит игру «Соревнование». – Сколько вам удастся решить примеров за одну минуту? Через минуту учитель определяет победителя игры. Задание № 13 (с. 33). – Дополните текст, придумайте вопрос так, чтобы получилась задача. Для того чтобы предложенный текст превратился в задачу, в случаях 1 и 2 детям необходимо придумать только вопрос. Например, в случае 1 вопросы могут быть такими: «Сколько ключей осталось в связке?», «На сколько меньше ключей отцепили, чем было в связке первоначально?», «На сколько больше ключей осталось в связке, чем отцепили?». Случай 3 принципиально отличается от предыдущих тем, что здесь уже недостаточно придумать только вопрос. Необходимо дополнить и условие, поэтому учащимся предоставляются большие возможности для фантазии. Желательно выслушать и разобрать как можно больше вариантов задач, предложенных детьми, и провести их сравнительный анализ. Задание № 12 (с. 33). – Прочитайте задачу. – Что известно? Что требуется узнать? – Запишите кратко условие задачи. Запись: 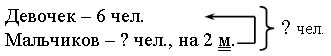 – Решите задачу по действиям. VI. Итог урока. – Что нового узнали на уроке? – Назовите крупную единицу длины. – Какие инструменты используют для измерения длины? Домашнее задание: № 9, 11 (учебник); № 41, 44 (рабочая тетрадь). Урок 14 Метр. Соотношения между единицами длины Цели урока: рассмотреть соотношения между единицами длины – метром, дециметром и сантиметром; познакомить учащихся с единицами длины на Руси; совершенствовать вычислительные навыки; формировать навыки решения задач разными способами; развивать умение анализировать. Ход урока I. Организационный момент. II. Устный счет. 1. Решите задачу. От дома до колодца 20 метров. Сколько метров надо пройти, чтобы принести ведро воды? А кружку воды? 2. Найдите примеры с ответом 13.
3. Решите задачу. Винни-Пух решил навестить ослика Иа. От дома до моста он прошел 20 метров, по мосту – 10 метров и от моста до домика Иа – еще 10 метров. Какова длина пути, который должен пройти Винни-Пух, чтобы навестить ослика Иа и вернуться домой? 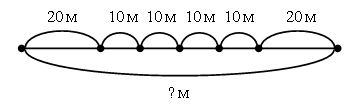 4. Какова масса каждого мешка с мукой? 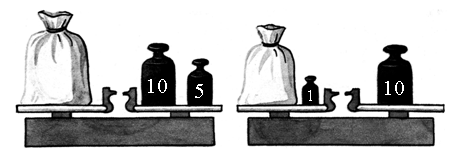 III. Сообщение темы урока. – Сегодня мы продолжим работу с единицами длины. Будем решать задачи на определение длины предметов. IV. Работа над новым материалом. 1. Практическая работа. – Измерьте длину своей парты. Сколько получилось сантиметров? – Сколько дециметров? – Покажите на рулетке отрезок 10 дм. – Как называется эта единица длины? (1 метр.) – Как можно начертить отрезок длиной 12 дм? Варианты выполнения задания: I вариант – можно отложить 1 дециметр двенадцать раз; II вариант – можно отложить 1 метр и еще 2 дециметра (так как 12 дм = 1 м 2 дм). – Какой вариант более рациональный? 2. Работа по учебнику. Задание № 5 (с. 31). – Прочитайте задание. Можно ли этот текст назвать задачей? – Придумайте вопрос задачи. Варианты вопросов: Какова длина всей ленты? (5 + 4 = 9.) На сколько метров один кусок длиннее (короче) другого? (5 – 4 = 1.) Учащиеся объясняют план решения каждой задачи. Задание № 6 (с. 31). Это задание развивает глазомер учащихся. На первый взгляд кажется, что жуки находятся на одинаковом расстоянии от финиша. Но это впечатление обманчиво. Выполнив измерения, учащиеся убеждаются, что жук под № 2 ближе к финишу, чем другой участник соревнования. Задание № 7 (с. 32). – Прочитайте условие задачи. Что вам известно? – Какой вопрос можно поставить к данному условию? Вопросы: Чему равна ширина комнаты? Чему равен периметр этой комнаты? 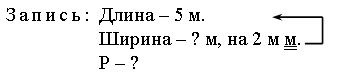 Решение: 1) 5 – 2 = 3 (м) – ширина. 2) 5 + 5 + 4 + 4 = 18 (м) – периметр комнаты. Ответ: 18 м. Задание № 8 (с. 32). Сначала лучше разобрать случай 2, так как выполнить это задание можно с опорой на модели. Попросите учащихся положить перед собой оранжевую и белую палочки. Длина оранжевой палочки – 10 см, или 1 дм, а белой – 1 см. Скажите детям, что роль рейки у нас будет играть оранжевая палочка, так как ее длина – 1 дм. Выложим вдоль оранжевой палочки белые палочки. Их получится ровно 10. 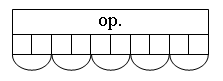 5 раз по 2 белые палочки Так как длина каждой белой палочки – 1 см, то видно, что в оранжевой палочке укладывается 5 раз по 2 см. Следовательно, чтобы получить 1 дм, надо от рейки отмерить 5 раз по 2 см. Теперь можно переходить к случаю 1. Предложите детям выполнить это задание самостоятельно. Но для того чтобы ученики могли действовать по аналогии со случаем 2, предварительно вспомните с ними, что 1 м – это 10 дм, а 20 см – это 2 дм.  V. Повторение пройденного материала. 1. Работа по учебнику. Задание № 15 (с. 34). – Прочитайте задачу. – Что вам известно? Что требуется узнать? – Сможете ли вы решить эту задачу? (Это задача с недостающими данными.) – Как надо изменить условие этой задачи, чтобы она имела решение? (Надо указать либо число подосиновиков, либо число подберезовиков, найденных в лесу.) – Можно ли выбрать любое число подосиновиков или подберезовиков? (Так как число подберезовиков на 8 больше, чем подосиновиков, то число подосиновиков мы можем выбрать произвольно, а вот число подберезовиков должно быть обязательно больше 8.) – Верно, если число подберезовиков равно 8, то тогда получается, что подосиновиков не нашли совсем (8 – 8 = 0), а это не соответствует условию задачи. Если же число подберезовиков меньше 8, например 6, то получается, что задача не имеет решения, так как невозможно вычислить число подосиновиков (6 – 8 = ?). – Придумайте недостающее данное и решите задачу самостоятельно. 2. Путешествие в прошлое. Как появились меры длины. Как измеряли на Руси – Нельзя представить себе жизнь человека, не производящего измерений: это и портные, и механики, и обыкновенные школьники. Сегодня мы все знакомы с линейкой, метром. А что же существовало до того, как все это изобрели? Первыми измерительными приборами были части тела: пальцы рук, ладонь, ступня. Так, у древних египтян основной мерой длины служил локоть (расстояние от конца пальцев до согнутого локтя). Он делился на семь ладоней, а ладонь на четыре пальца. (Учитель показывает, как измеряют локтем длину ленты, а затем предлагает проделать это двум-трем ученикам. Количество локтей получилось разное.) – Чтобы измерения были более точными и не зависели от роста людей, в Древнем Египте придумали образцовые меры: локоть, ладонь, палец. Теперь было уже неважно, какой длины локоть или ладонь у человека, он измерял не своим, а общим локтем, т. е. условной палочкой. В Англии также существовали единицы длины, связанные с частями тела человека: дюйм (2,54 см) в переводе с голландского означает «большой палец»; фут (30 см 48 мм, или 12 дюймов) в переводе с английского – «нога»; ярд – это расстояние от носа короля Генриха I до конца среднего пальца его вытянутой руки. Многие народы измеряли длину шагами, двойными шагами, тростями. Очень большие расстояния измерялись переходами, привалами или даже днями. В Японии существовала мера, называемая лошадиным башмаком. Она была равна пути, в течение которого изнашивалась соломенная подошва, привязанная к копытам лошади. У многих народов расстояние определялось длительностью полета стрелы или пушечного ядра. До сегодняшнего дня сохранилось выражение «не подпустить на пушечный выстрел». – А кто знает, какие меры длины использовали издавна на Руси? (Сажень (маховая, косая), верста, локоть, аршин.) О локте мы уже говорили. Маховая сажень (1,76 м) – расстояние между раскинутыми в стороны руками. Косая сажень (2,48 м) – расстояние от каблука правой ноги до кончиков пальцев вытянутой вверх левой руки. Слово аршин пришло с Востока. Приезжие купцы торговали невиданными тканями: китайским шелком, индийской парчой, бархатом, которые отмеряли аршинами (с персидского – «локоть»). Он равен 71 см. Учитель может предложить следующие вопросы-задания: 1. Измерить длину парты в локтях, ладонях. 2. Какого роста была Дюймовочка? 3. Каков был рост человека, про которого говорят «от горшка два вершка»? 4. 7 футов под килем – это сколько метров? Для выполнения этого задания удобно пользоваться следующей таблицей:
Задание № 18 (с. 35). – Прочитайте старинную задачу. – Что вам известно? Что требуется узнать? – Какую новую единицу длины содержит эта задача? (Аршин.) 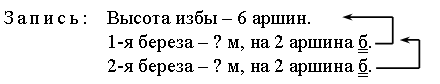 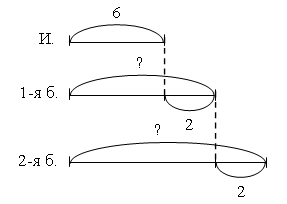 I способ: 1) 6 + 2 = 8 (аршин) – высота 1-й березы. 2) 8 + 2 = 10 (аршин) – высота 2-й березы. II способ: 1) 2 + 2 = 4 (аршина) – выше 2-я береза, чем изба. 2) 6 + 4 = 10 (аршин) – высота 2-й березы. Ответ: 10 аршин. 3. Фронтальная работа. – Рассмотрите чертеж. Как называется данное геометрическое тело? (Пирамида.) Учитель демонстрирует модель пирамиды. – Сравните данную модель пирамиды с ее чертежом в тетради. – Сколько всего граней у пирамиды? (Пять.) – Сколько граней вы видите на модели? (Две.) – Какие это грани? (Боковые.) – Сколько невидимых граней на модели? (Три.) – Какие это грани? (Две боковые грани и одна нижняя, т. е. основание.) – Сколько граней нужно раскрасить на чертеже? (Три.) После этого учитель предлагает раскрасить невидимые грани пирамиды на чертеже. (Раскрашенным окажется весь чертеж.) 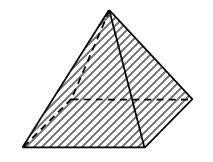 4. Работа в печатной тетради № 1. Задание № 47. – Какие числа ввели в «машину»? 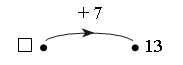 Учащиеся. В «машину» ввели неизвестное число. Машина прибавила к нему 7. Вышло из «машины» число 13. К неизвестному числу стрелка не идет. Изображаем «машину», обратную данной: –7. 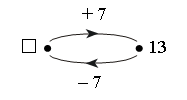 Идем по стрелке: 13 – 7. Выполняем вычисление. Получаем 6. Значит, неизвестное число 6. Записываем его в «окошко». Выполняем проверку. Идем по верхней стрелке: 6 + 7 = 13 (верно). VI. Итог урока. – Что нового узнали на уроке? – Назовите старинные русские единицы длины. – Назовите признаки пирамиды. Домашнее задание: № 14, 16 (учебник); № 46, 49, 51 (рабочая тетрадь). Урок 15 Многоугольник и его элементы Цели урока: ввести понятие «многоугольник»; научить находить и показывать вершины, стороны и углы многоугольника; рассмотреть обозначение многоугольника латинскими буквами; совершенствовать навыки решения задач; развивать внимание и пространственное мышление. Ход урока I. Организационный момент. II. Устный счет. 1. Имя какого сказочного героя здесь зашифровано?
2. Нарисуйте недостающую фигуру, чтобы в каждом ряду были фигуры разной формы. 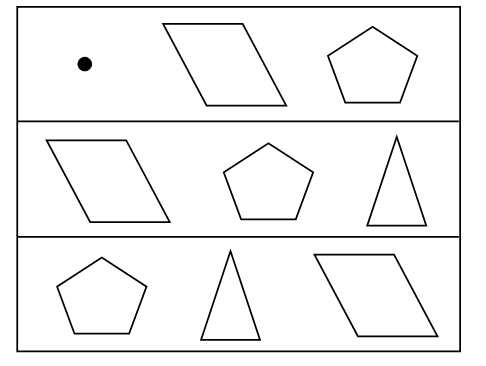 3. Сравните тексты задач. Чем они похожи? Чем отличаются?
– Можно ли утверждать, что решения этих задач одинаковы? |
