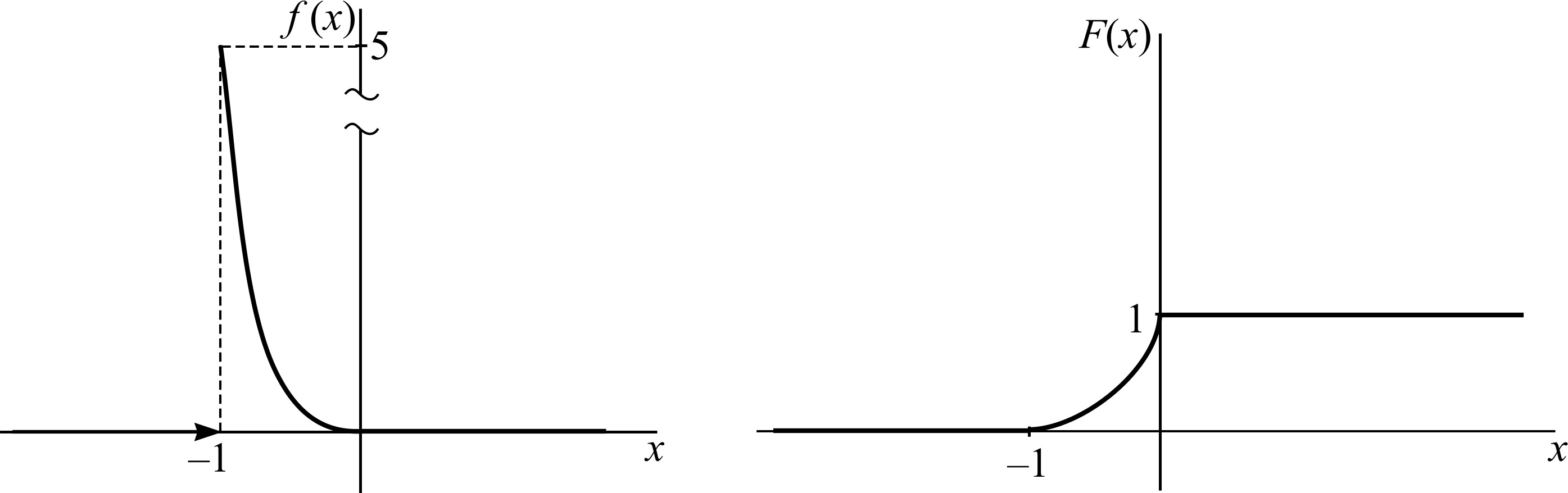Вечернего и заочного обучения

• Название: Вечернего и заочного обучения
• Анкор: DE2AAC829C40403EA2B1245CEFB6E2D1.doc
• Дата: 21.07.2018
• Размер: 0.85 Mb.
• Имя файла: DE2AAC829C40403EA2B1245CEFB6E2D1.doc
• Тип: Контрольная работа; #21800
• страница: 6 из 8

Случайные величины

Пример 4. Дана корреляционная таблица случайного вектора
(X, Y).

X Y	–1	2
1	0,1	0,2
3	0,4	P22

Найти: P₂₂; F(2,2); ряды распределения X, Y; P(X  1); P(1,5  X < 4); M[X]; D[X]; M[Y]; D[Y]; F(x); график F(x) и многоугольник распределения; зависимы X и Y или нет; коэффициент корреляции r[x,y]; линию регрессии Y по X.

Из условия нормировки: 0,1 + 0,2 + 0,4 + P₂₂ = 1, P₂₂ = 0,3.

Значение функции распределения F(2,2) = P(X < 2; Y < 2) = 0,1.

Случайная величина X принимает значения 1; 3, причем

P(x = 1) = P(1; –1) + P(1; 2) = 0,1 + 0,2 = 0,3;

P(x = 3) = P(3; –1) + P(3; 2) = 0,4 + 0,3 = 0,7.

Ряд распределения X
X 1 3 Px 0,3 0,7	P(X  1) = P(1) = 0,3; P(1,5  X < 4) = P(3) = 0,7;

M[X] = 1  0,3 + 3 0,7 = 2,4;

D[X] = M[X²] – (M[X])² = (1  0,3 + 9  0,7) – 2,4² = 6,6 – 5,76 = 0,84.

Ряд распределения Y

Y	–1	2
Py	0,5	0,5

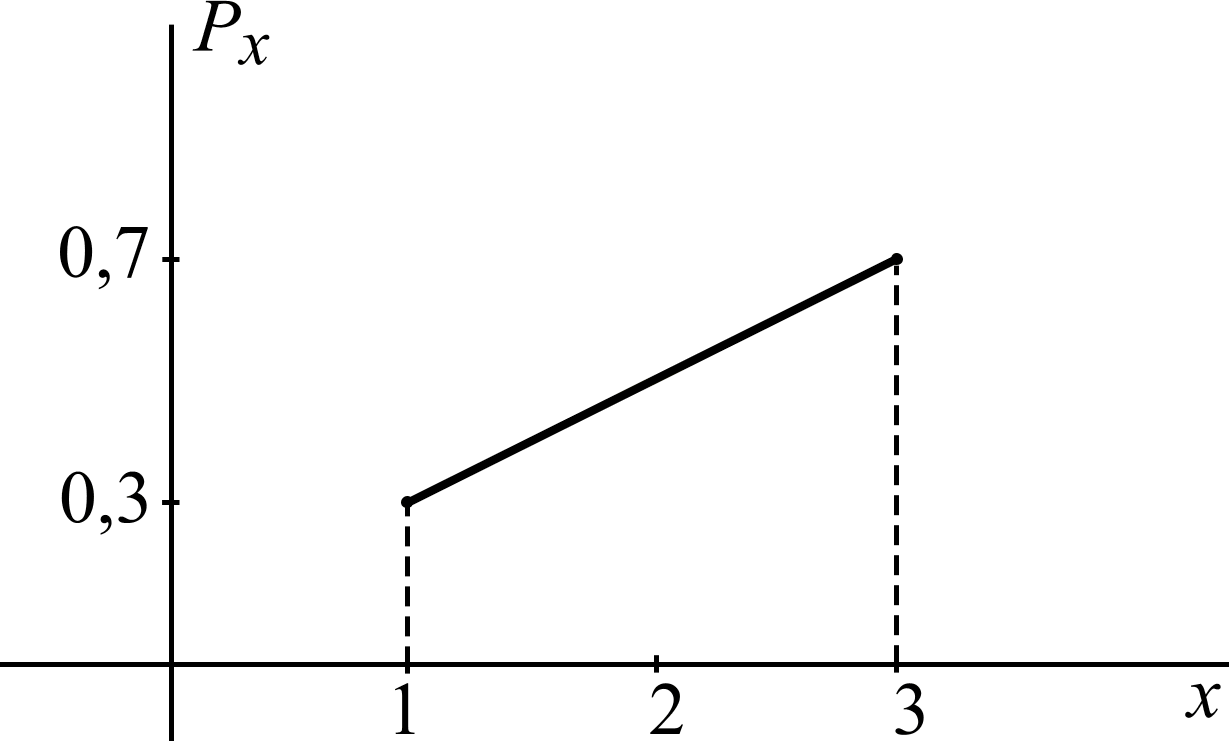
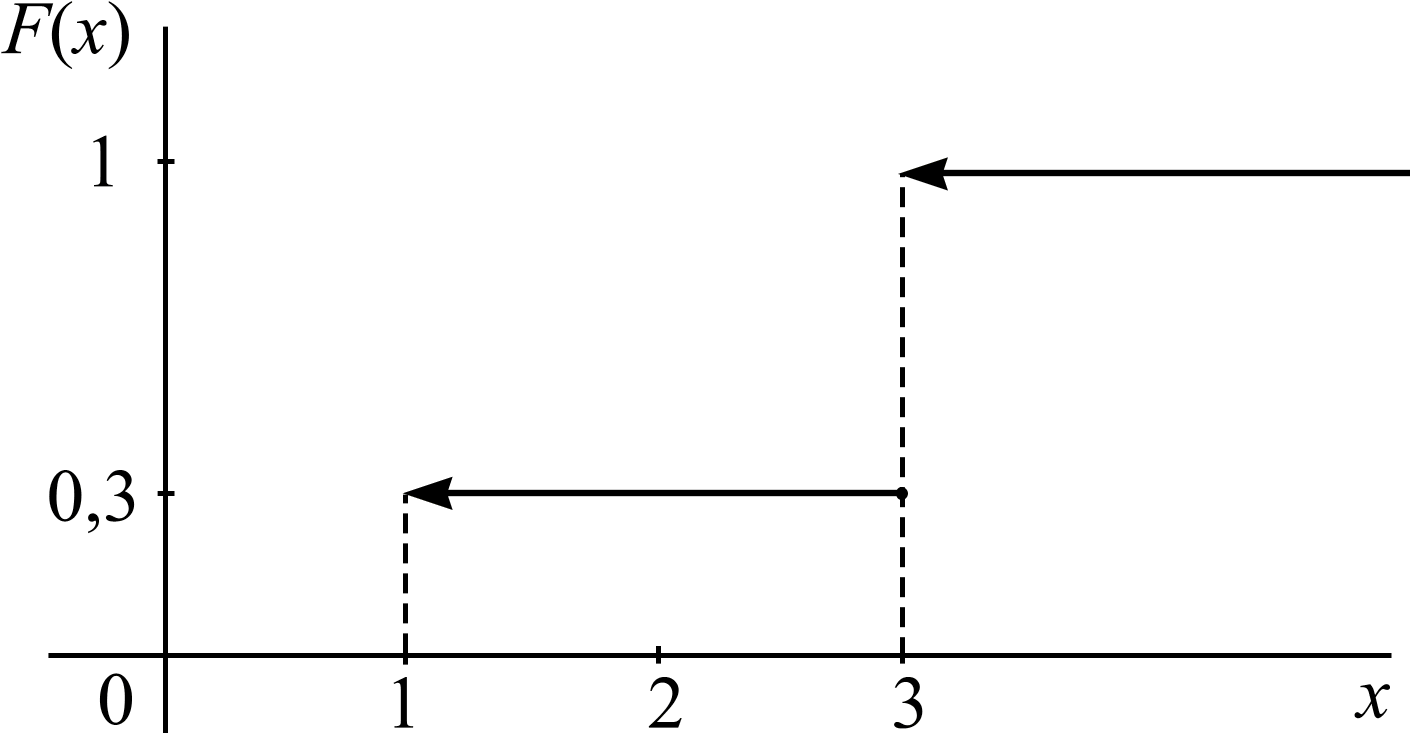
M[Y] = –1  0,5 + 2  0,5 = 0,5;

D[Y] = M[Y²] – (M[Y])² = 1  0,5 + 4  0,5 – 0,25 = 1,75.

Функция распределения F(x) = P(X < x):

F(x) = 0 при x  1;

F(x) = P(1) = 0,3 при 1 < x  3;

F(x) = P(1) + P(3) = 1 при 3 < x.

Окончательно: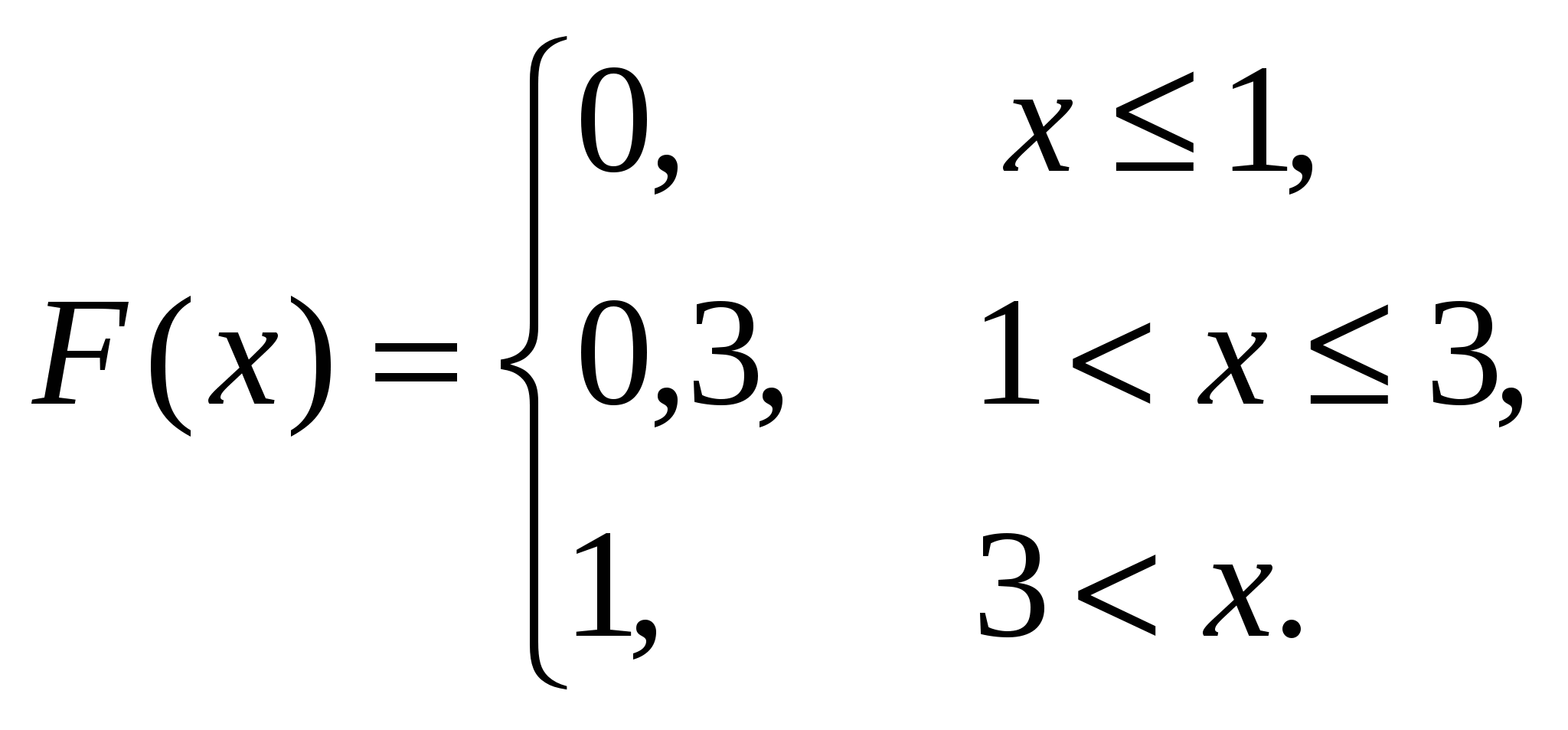



Изобразим многоугольник распределения (рис. 8) и график функции распределения F(x) (рис. 9).

Рис. 8	Рис. 9

Случайные величины X и Y независимы, если P(X = x_i; Y = y_j) = = P(X = x_i)  P(Y = y_j).

Проверим для всех i и j эти равенства:

P(X = 1)  P(Y = –1) = 0,3  0,5 = 0,15; P(X = 1; Y = –1) = 0,1.

Равенство не выполнено, случайные величины X и Y зависимы.

Найдем ;

K[X,Y] = M[X  Y] – M[X]  M[Y] = 1  (–1)  0,1 +

+ 1  2  0,2 + 3  (–1)  0,4 + 3  2  0,3 – 2,4  0,5 = 0,9 – 1,2 = –0,3.

Найдем условные ряды распределения Y по X.
Y –1 2	Y –1 2

Найдем условные математические ожидания Y по X:





Нарисуем линию регрессии Y по X(рис. 10).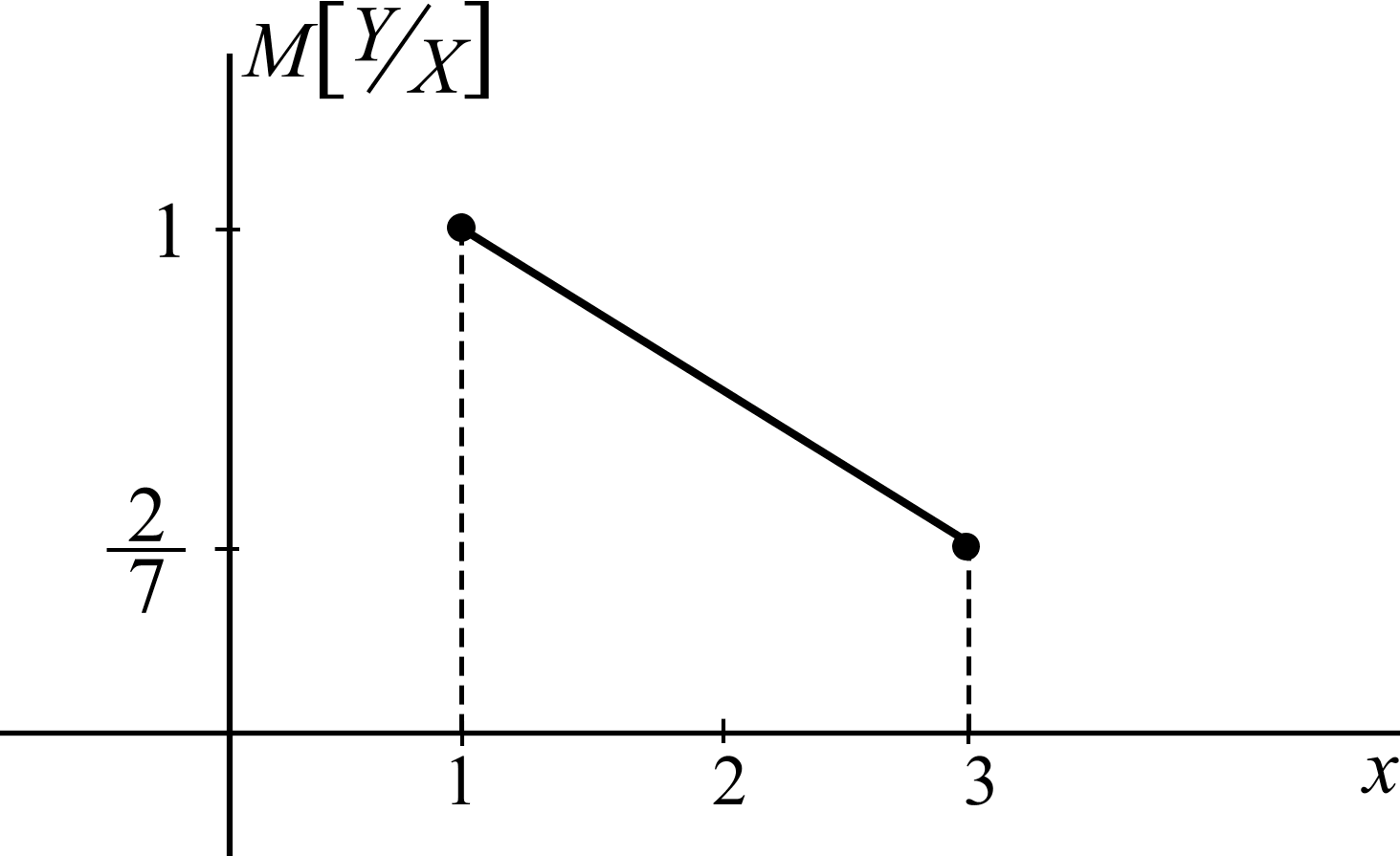



Рис. 10

Если r[X,Y] < 0, то зависимость Y от X убывающая, что видно из линии регрессии.

Пример 5. Дана функция распределения непрерывной случайной величины X: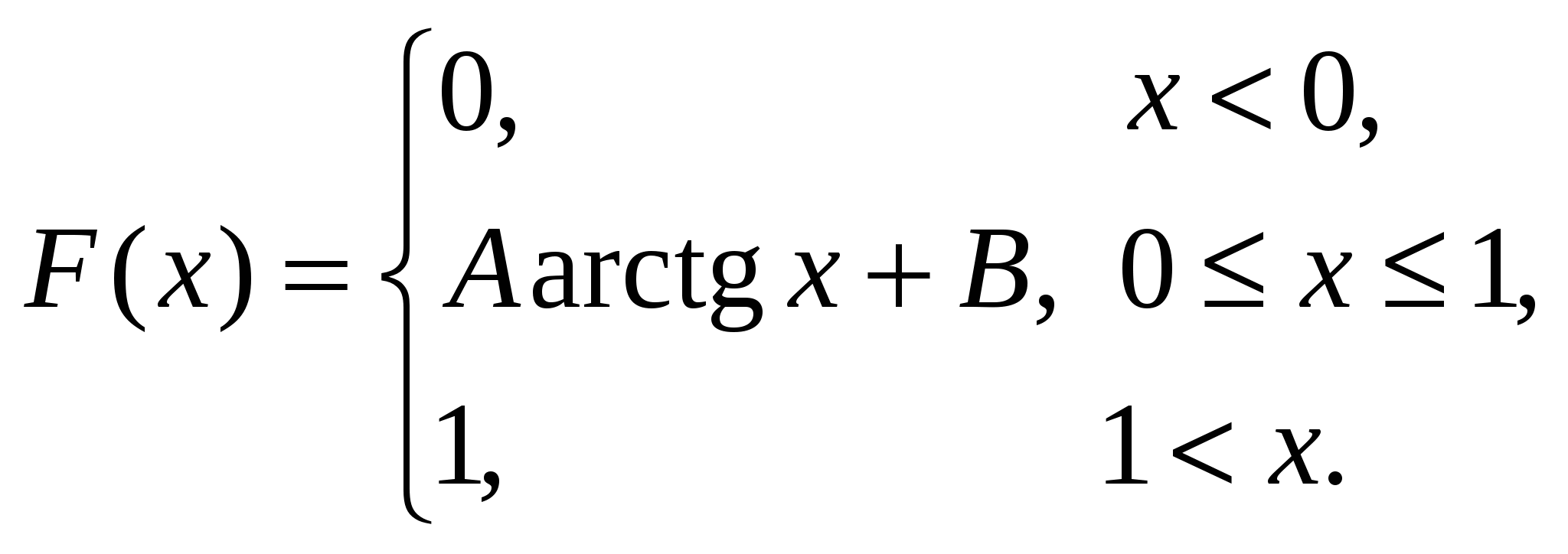



Найти: А и В; M[X], D[X].

Для непрерывной случайной величины функция распределения непрерывна, поэтому

F(–0) = F(+0); F(1 – 0) = F(1 + 0);

0 = A arctg 0 + B; A arctg 1 + B = 1,

откуда 0 = В; 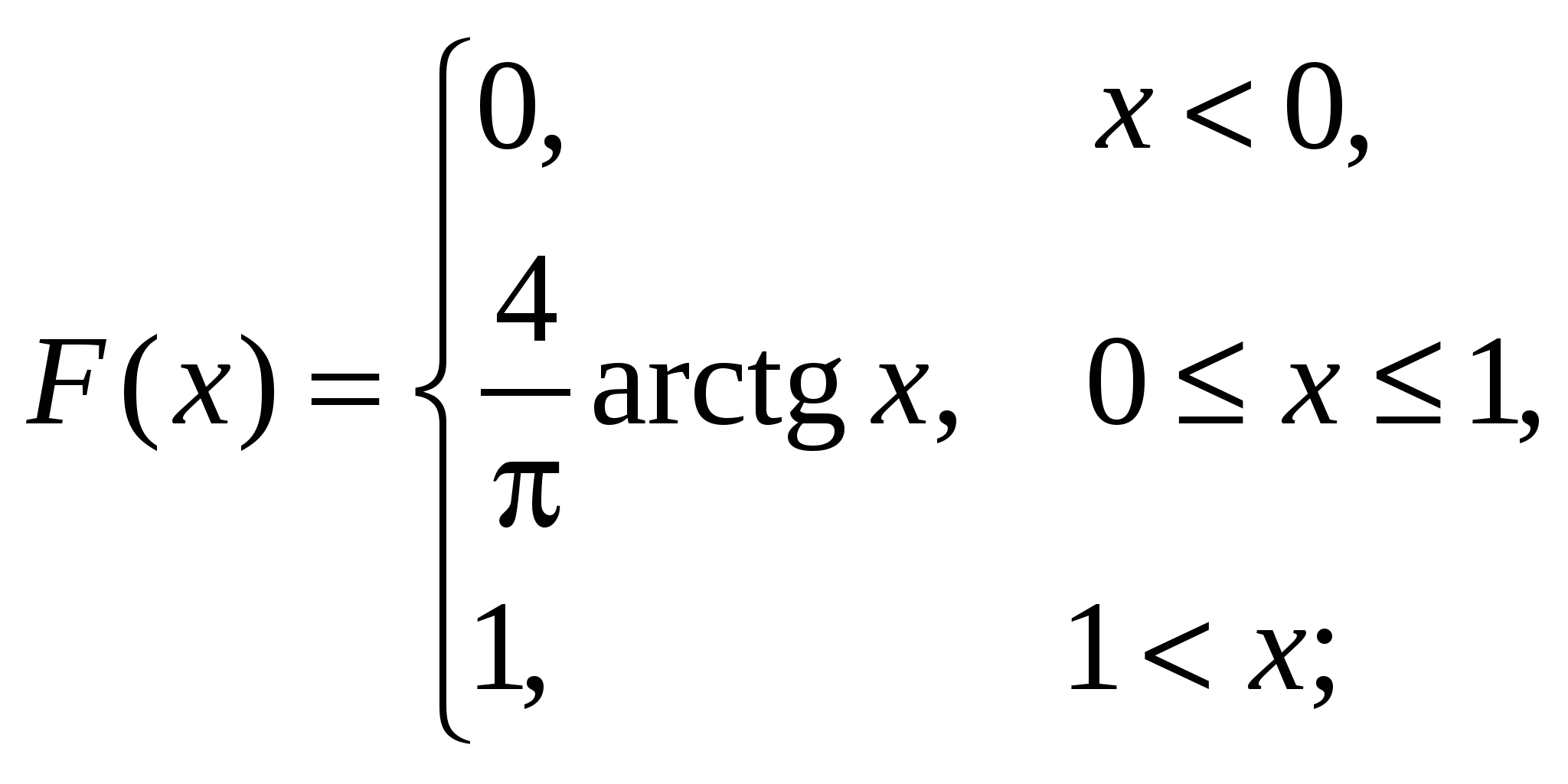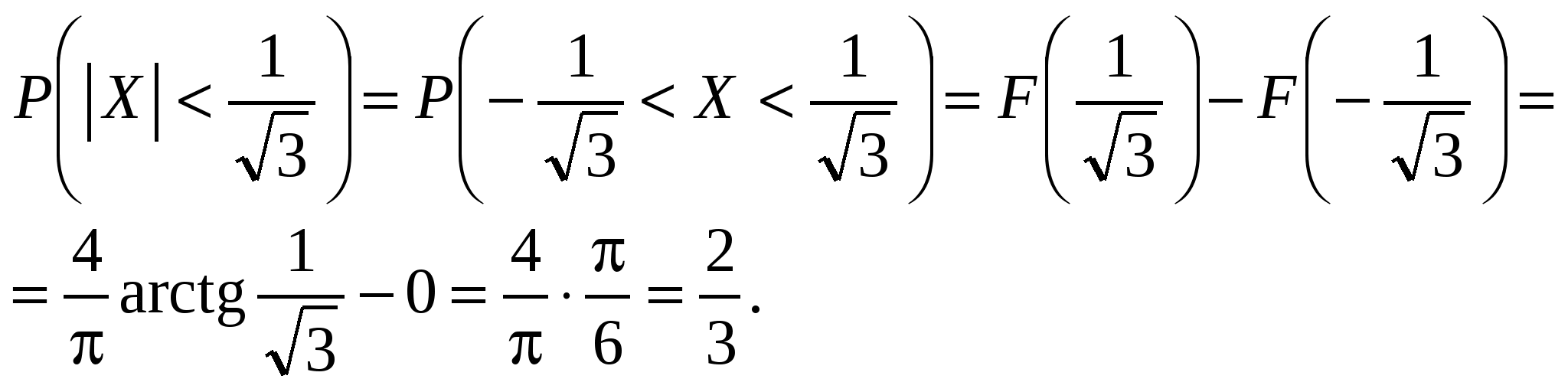следовательно, B = 0; ;





Найдем плотность распределения: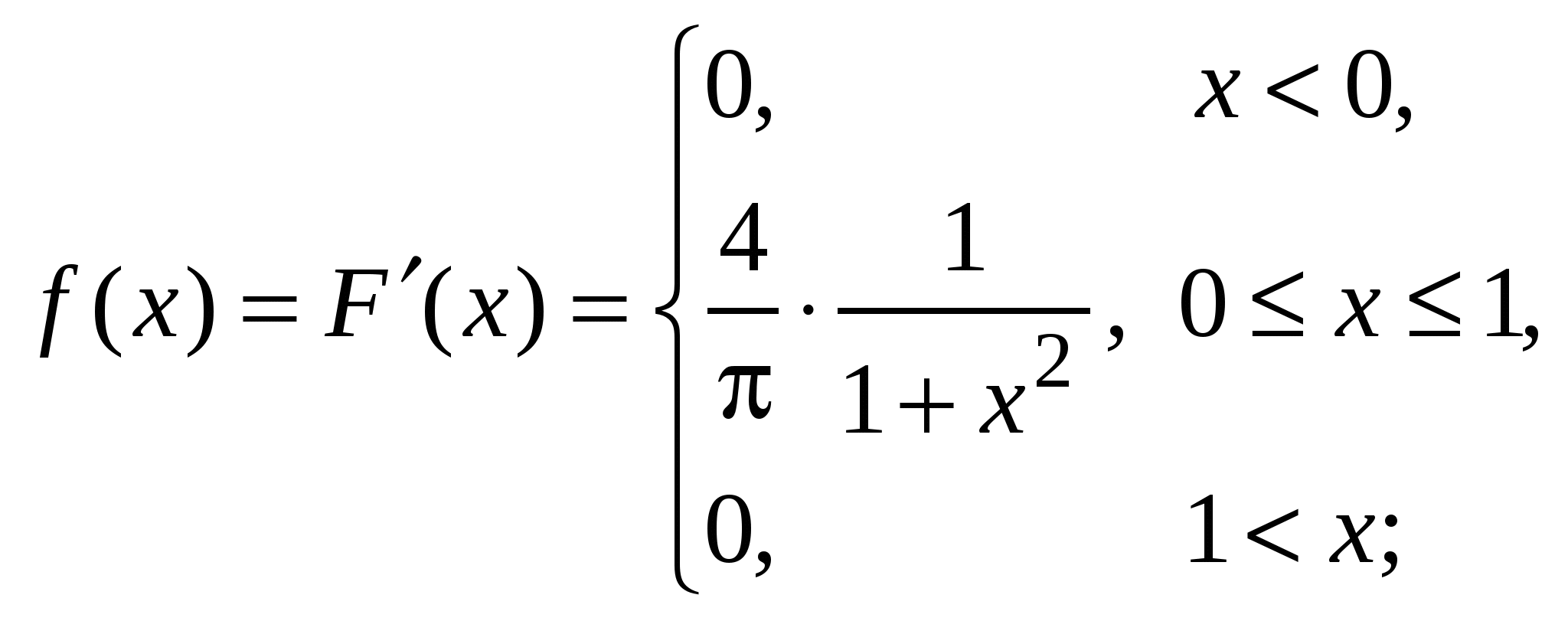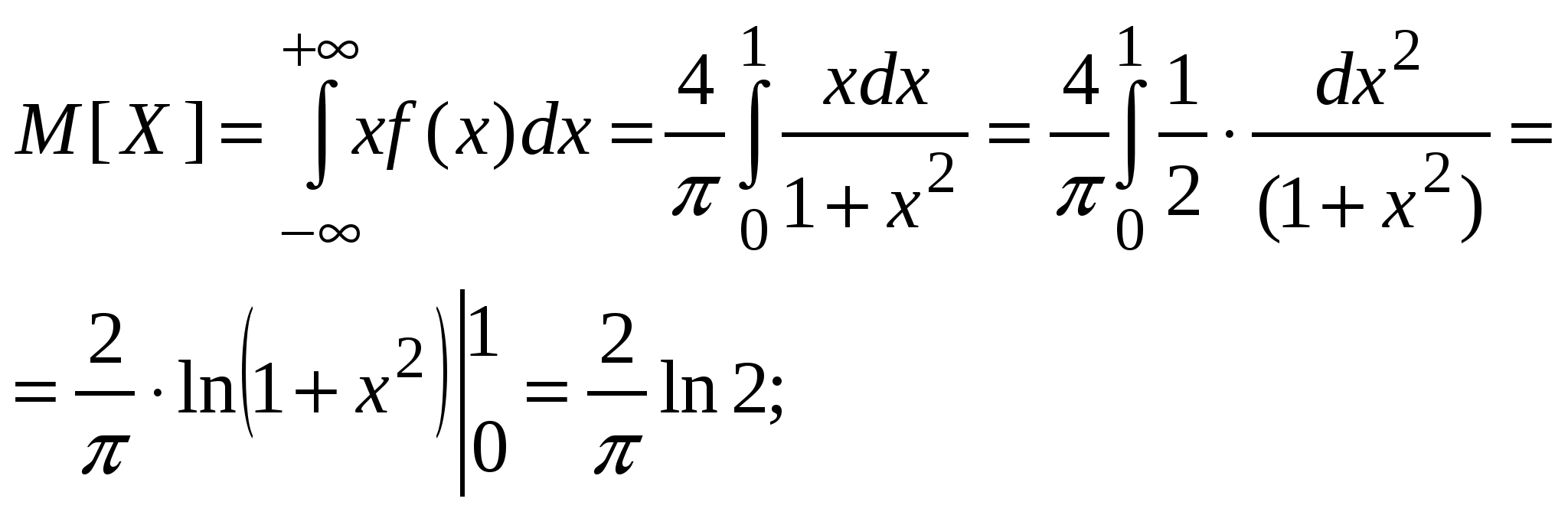





D[X] = M[X²] – (M[X])²;



поскольку

Пример 6. Дана плотность распределения непрерывной случайной величины X: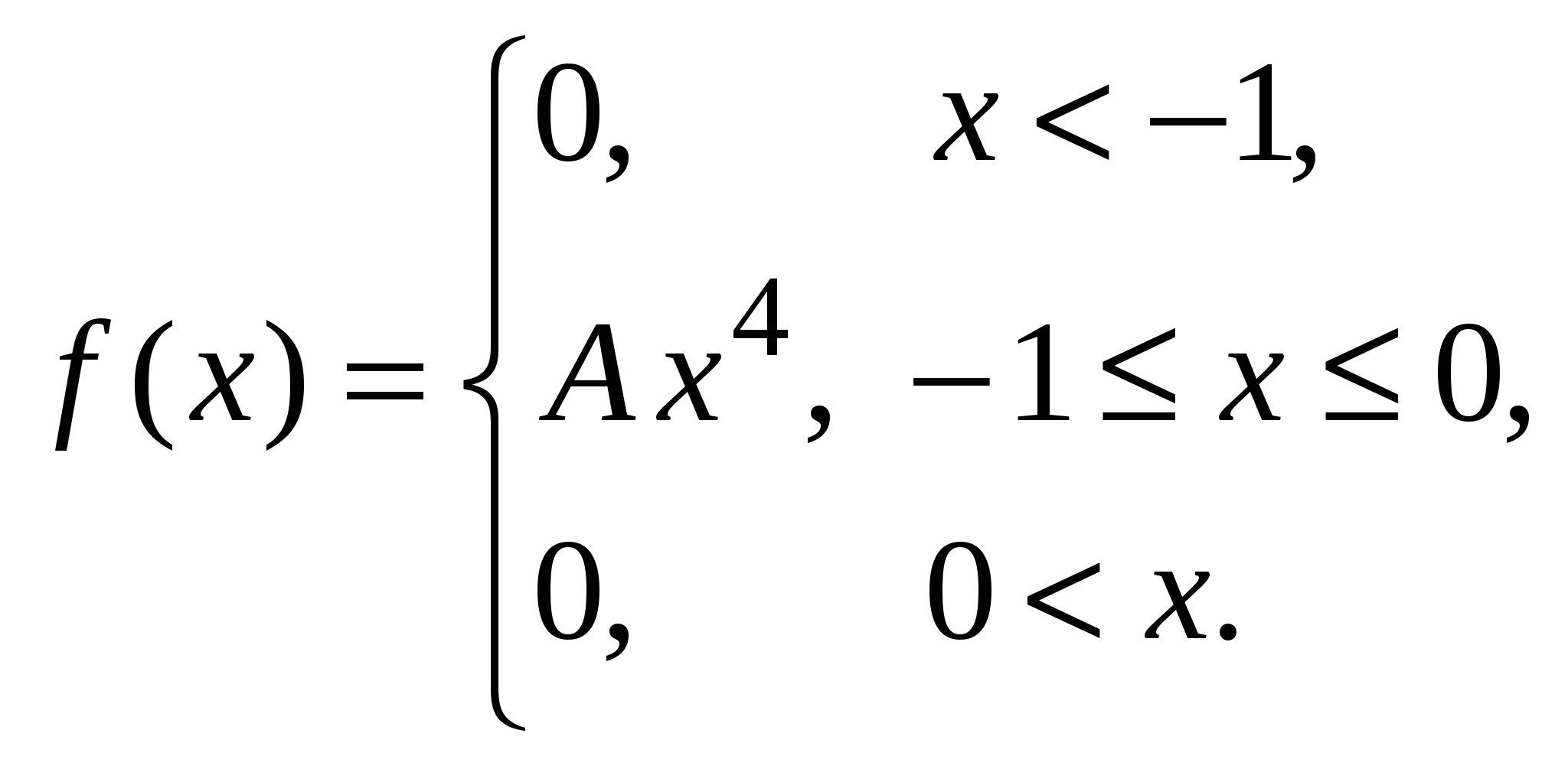



Найти: А, P(X > 0,5), F(x), графики f(x) и F(x).

Из условия нормировки полу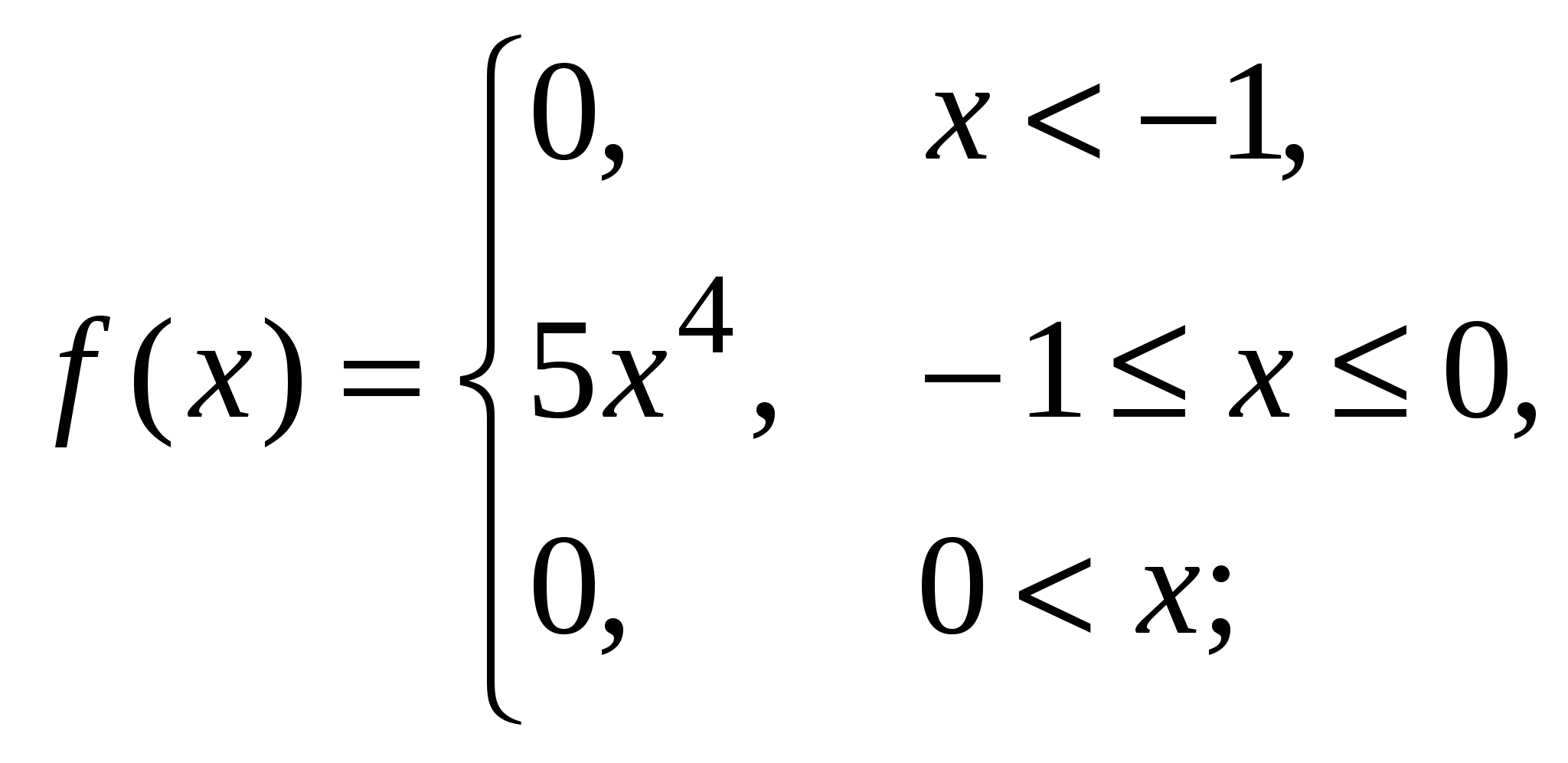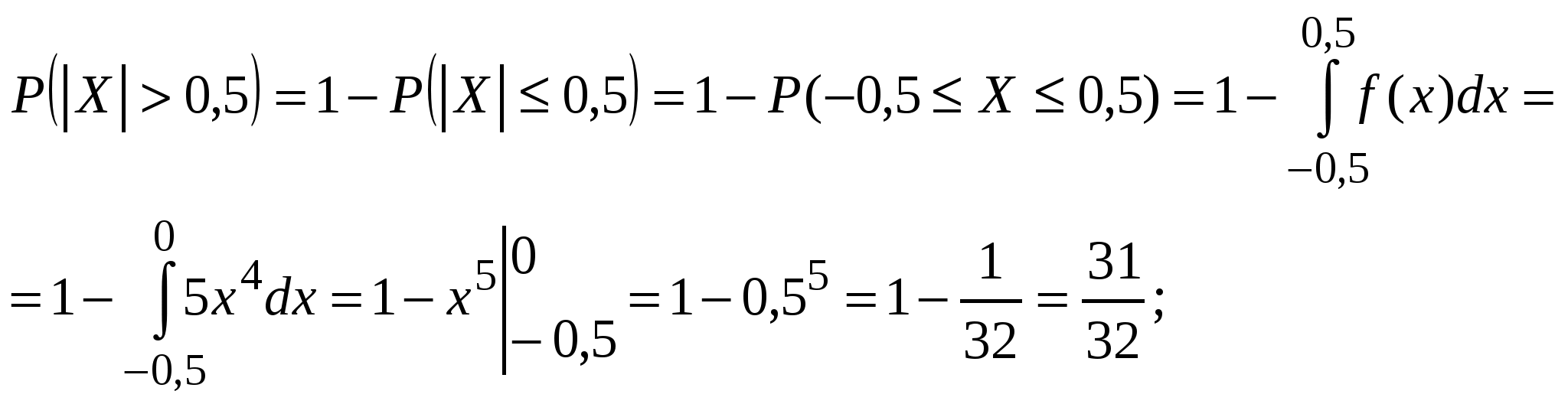чаем:



Итак:





F(x) = 0 при x < –1;

при –1  x  0;

при x < 0.

Окончательно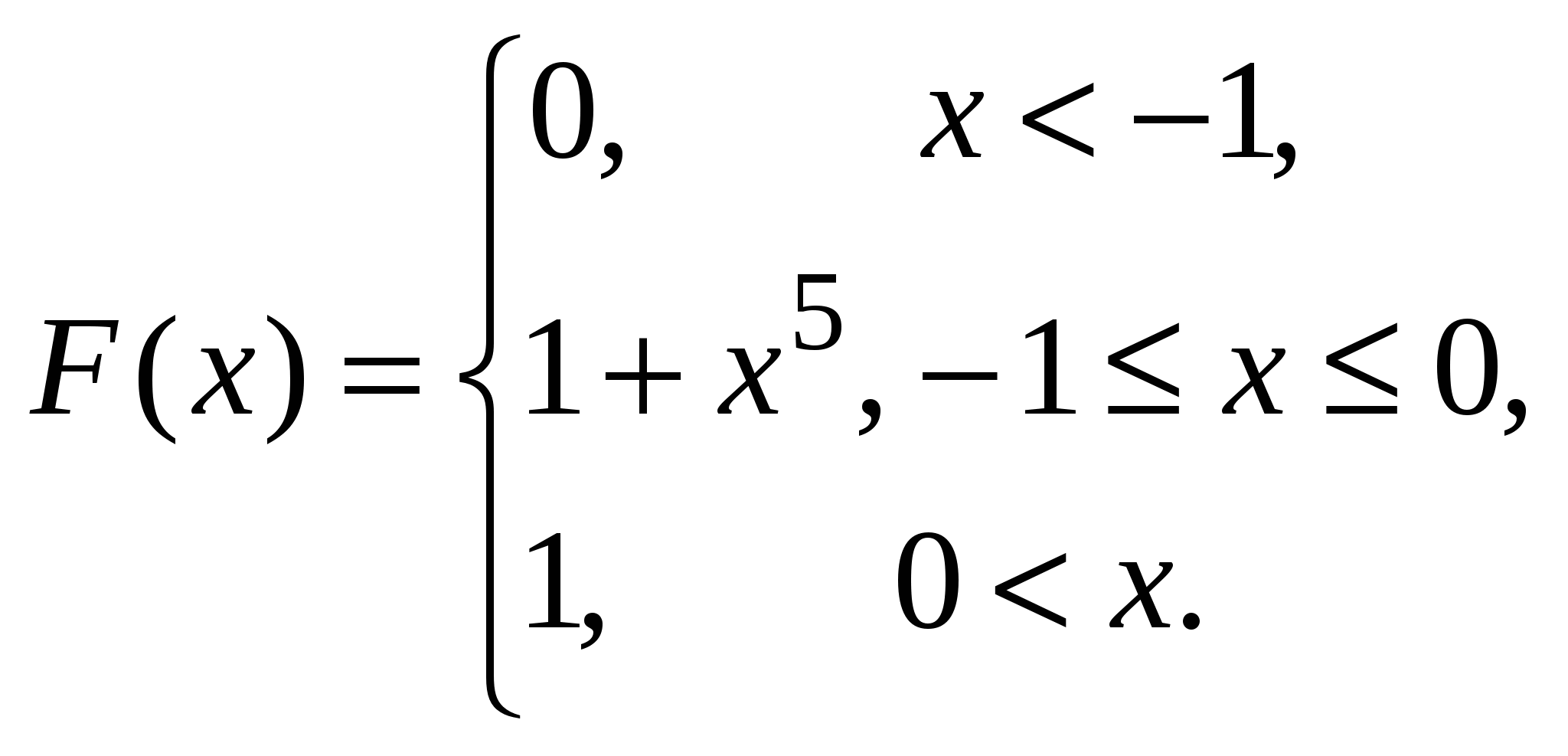

Графики f(x), F(x) представлены на рис. 11, 12.

Рис. 11	Рис. 12