Вечернего и заочного обучения
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
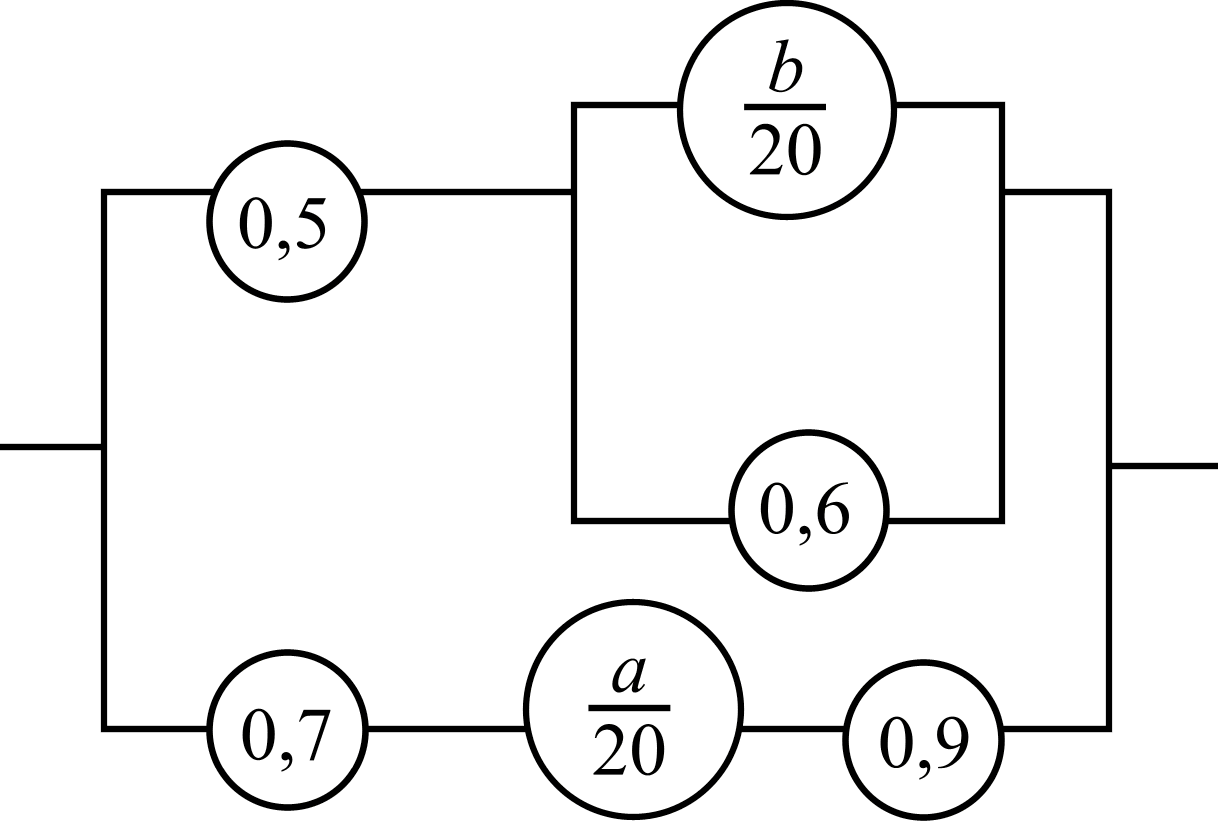
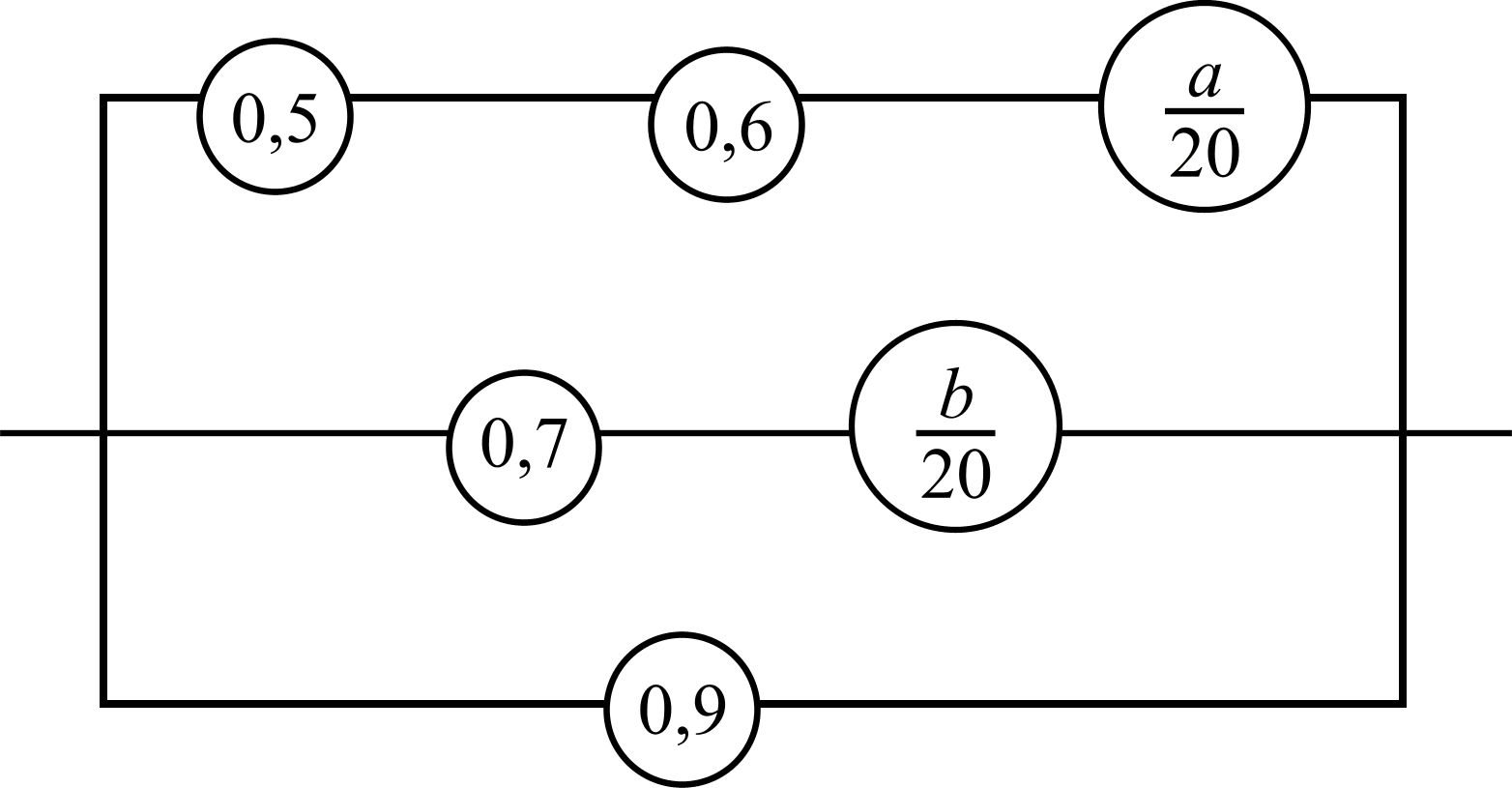
Контрольная работаВ условиях заменить параметр а – суммой предпоследней цифры номера вашей зачетки и 1; параметр b – суммой последней цифры и 1. 1. В партии а бракованных и (b+3) небракованных изделий. Наудачу взяты 4 изделия. Найти вероятность того, что среди них: а) одно бракованное; б) хотя бы одно бракованное; в) бракованных и небракованных поровну. 2. В первом ящике (а+4) белых и (b+1) черных шаров, а во втором ящике b – белых и (а+1) – черных шаров. Из первого ящика во второй переложили два шара: а) после перекладывания из второго ящика вынуты 3 шара. Какова вероятность того, что среди них 1 черный? б) после перекладывания из второго ящика вынуто 2 белых и 1 черный шаров. Найти вероятность того, что переложены шары разных цветов. 3. Стрелок произвел (b+5) выстрелов. Вероятность попадания при каждом выстреле равна 1/(2а). Найти вероятность того, что: а) было 2 попадания; б) было не более (3 + (–1)b + (–1)а) попаданий; в) было хотя бы одно попадание. 4. Найти надежность цепи, если надежности элементов указаны на схеме (рис. 4, 5)
5. Дан ряд распределения дискретной случайной величины X.
Найти: p3; M[X]; D[X]; P(–1 X b); F(x); графики многоугольника и функции распределения. 6. Дана плотность вероятности непрерывной случайной величины X.
Найти: c; M[X]; D[X]; P(–1 < X < b); F(x); графики f(x), F(x). 7. Дана функция распределения непрерывной случайной величины X: 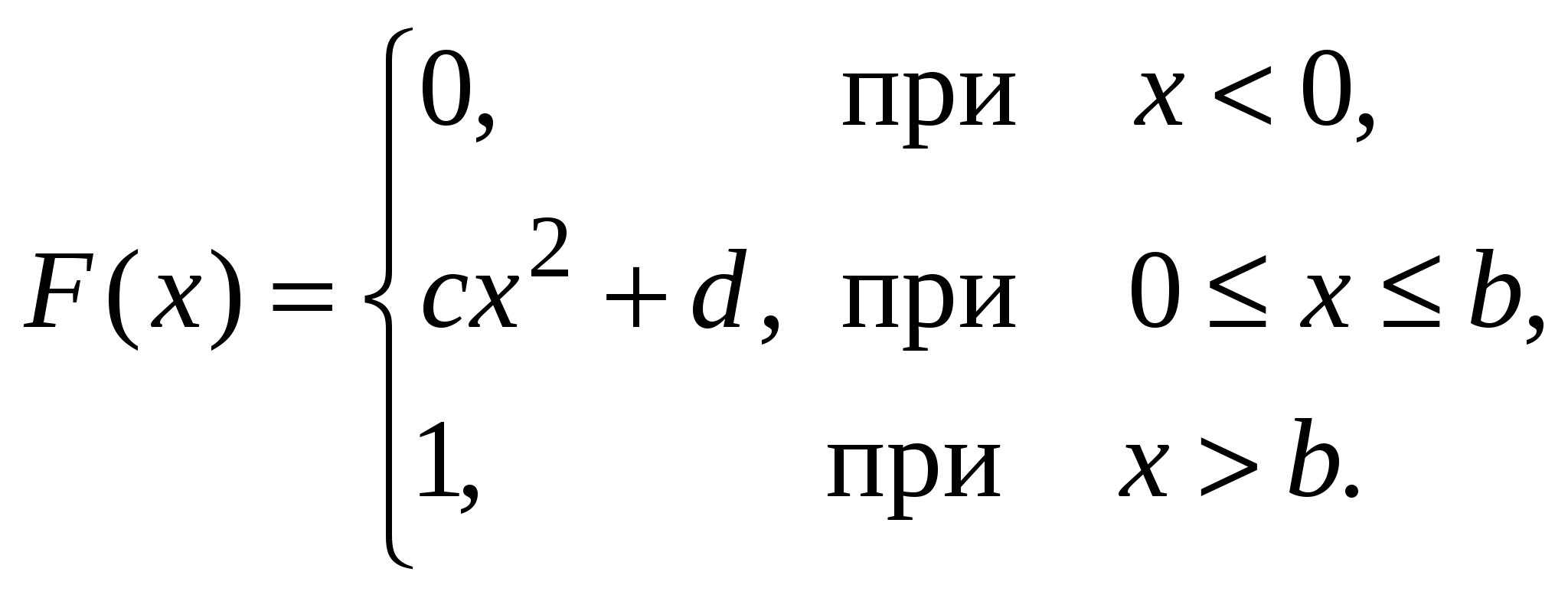 Найти: d; c; P(X> 0,5); M[X]; D[X]; f(x); графики f(x) и F(x). 8. Дана корреляционная таблица случайного вектора (X,Y).
Найти: P22; зависимы X и Y или нет; F(1,a); rxy; линию регрессии Y по X. |

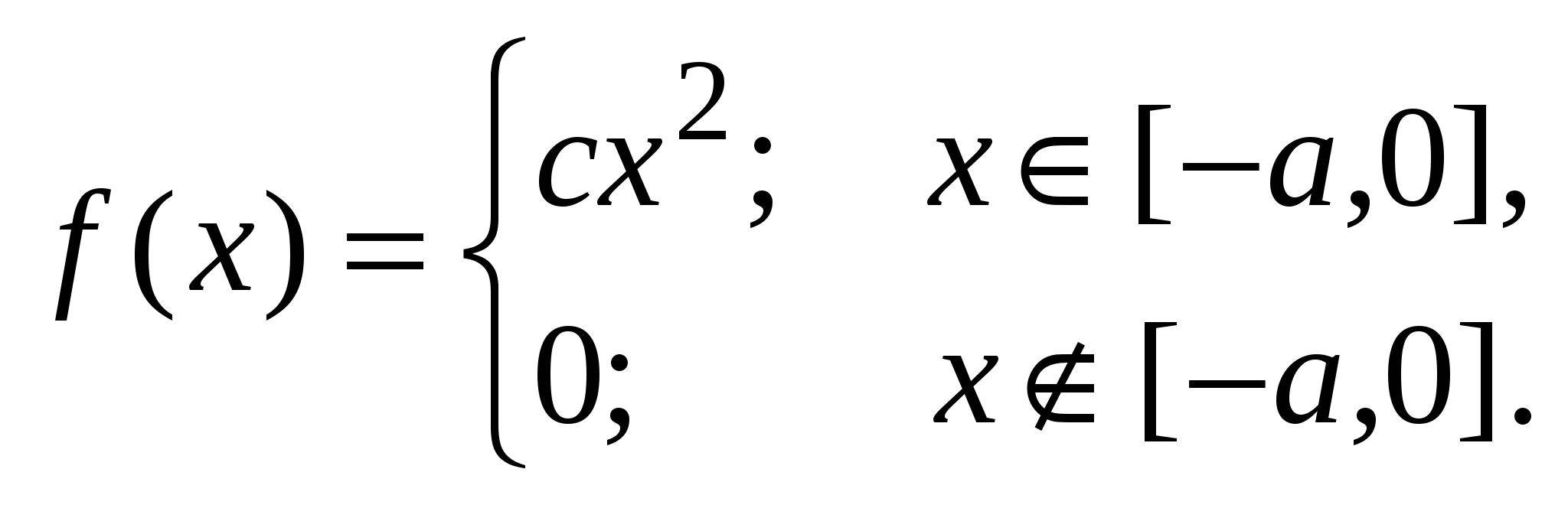
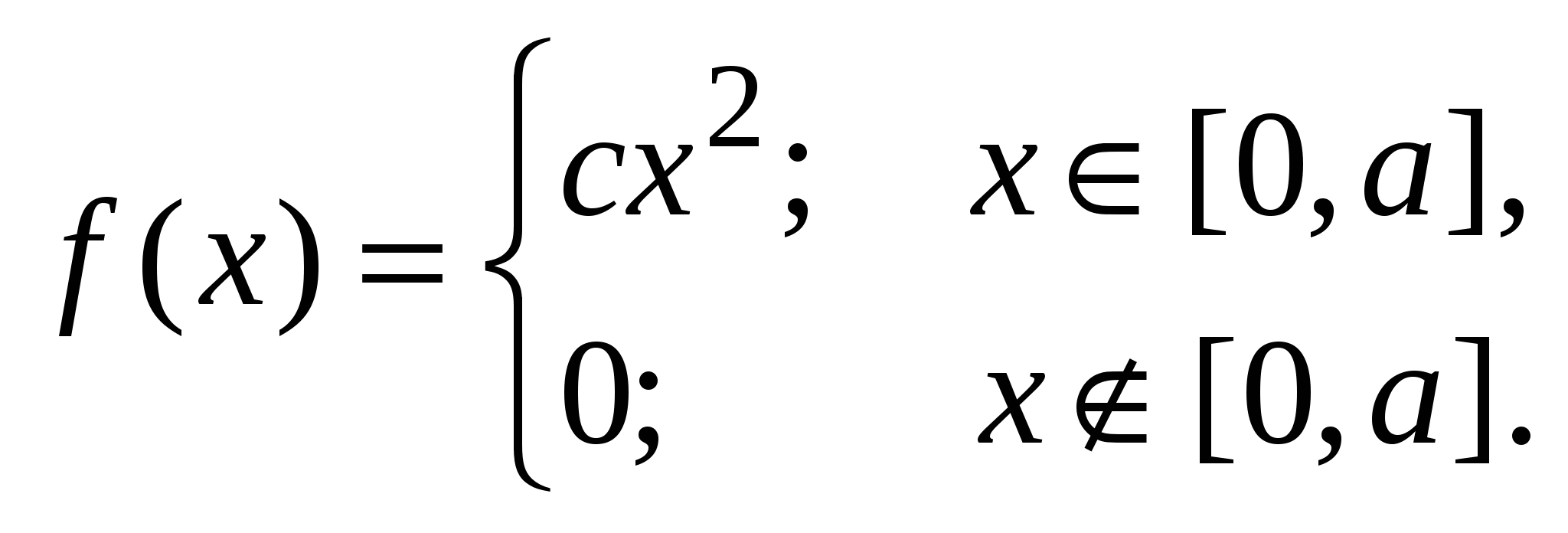
 Y
Y