Вечернего и заочного обучения

• Название: Вечернего и заочного обучения
• Анкор: DE2AAC829C40403EA2B1245CEFB6E2D1.doc
• Дата: 21.07.2018
• Размер: 0.85 Mb.
• Имя файла: DE2AAC829C40403EA2B1245CEFB6E2D1.doc
• Тип: Контрольная работа; #21800
• страница: 2 из 8

2. Случайные величины

Дискретные случайные величины	Непрерывные случайные величины
2.1. Законы распределения
Функция распределения F(x) = P(X < x), неубывающая.
F(x) – ступенчатая.	F(x) – непрерывная.
Ряд распределения X xi … xn P pi … pn	Плотность распределения f(x) = F(x);
Pi > 0.	f(x)  0.
Условия нормировки:
.
2.2. Числовые характеристики
Математическое ожидание:
Дисперсия:
D[X] = M[(X – M[X])2] = M[X2] – (M[X])2;

Дискретные случайные величины	Непрерывные случайные величины
2.3. Примеры случайных величин
Биноминальное распределение:	Равномерное распределение (рис. 1):
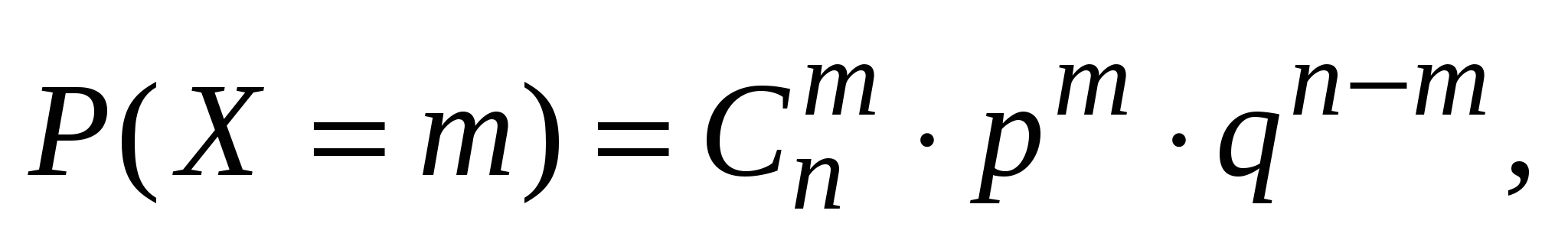
q = 1 – p; 0 < p < 1; 0  m  n;
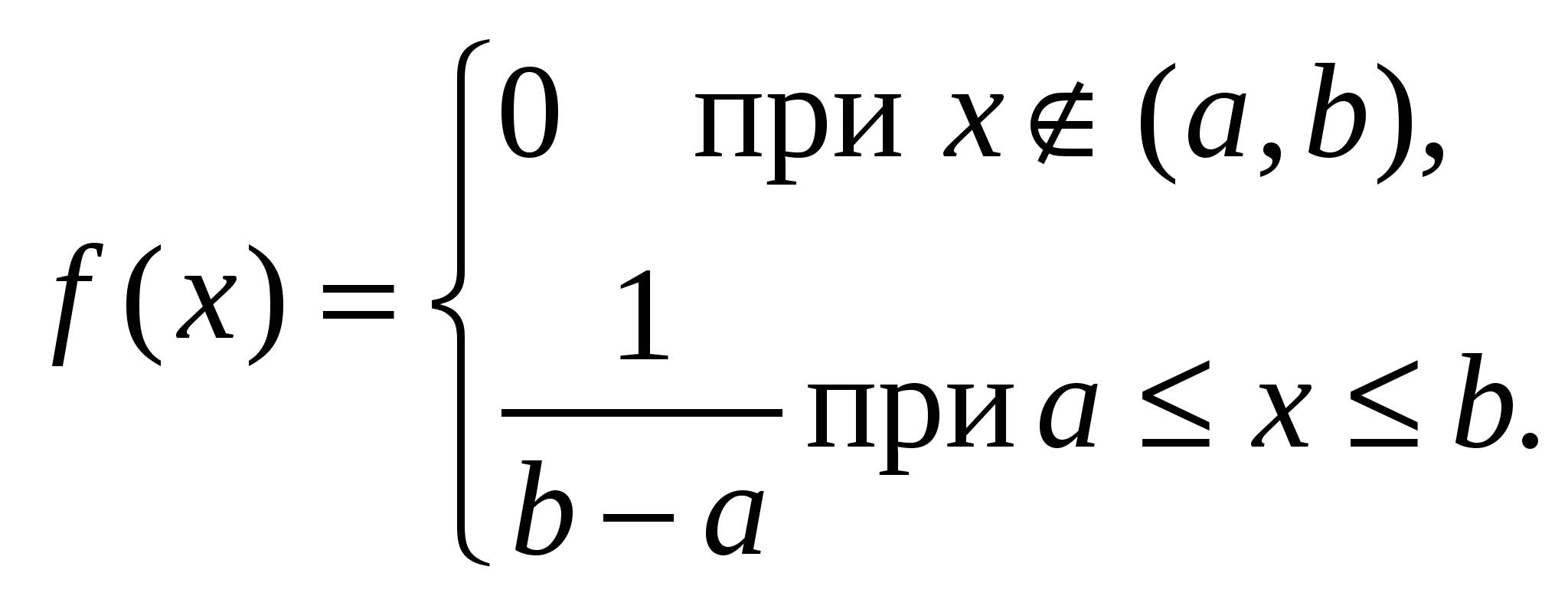
M[X] = n  p, D[X] = n  p  q.
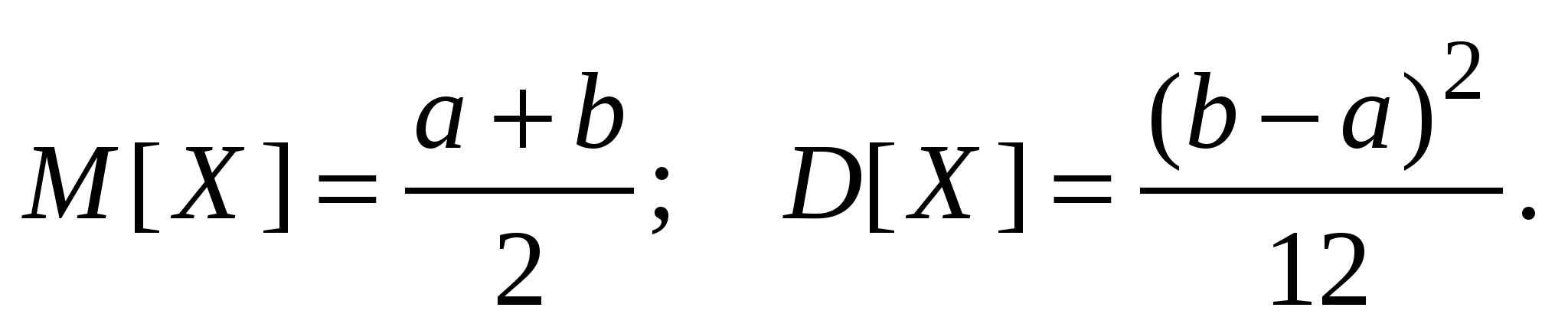
Пуассоновское распределение:	Показательное распределение (рис. 2):
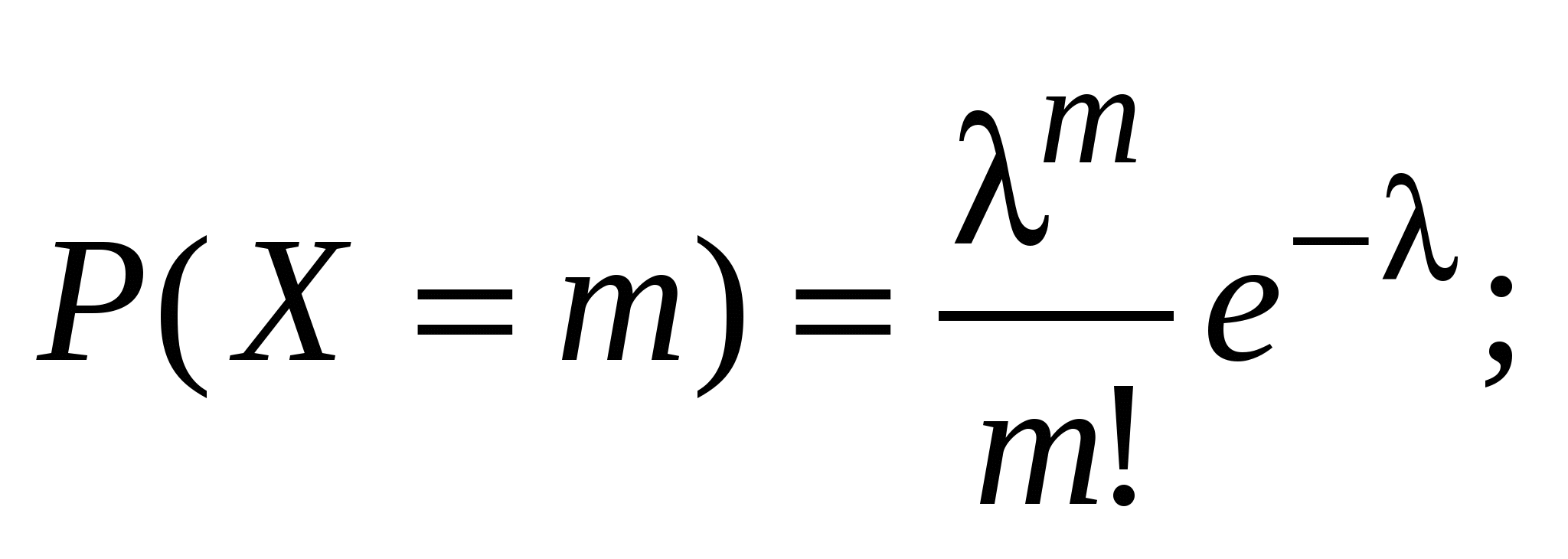
 > 0; 0  m < +;
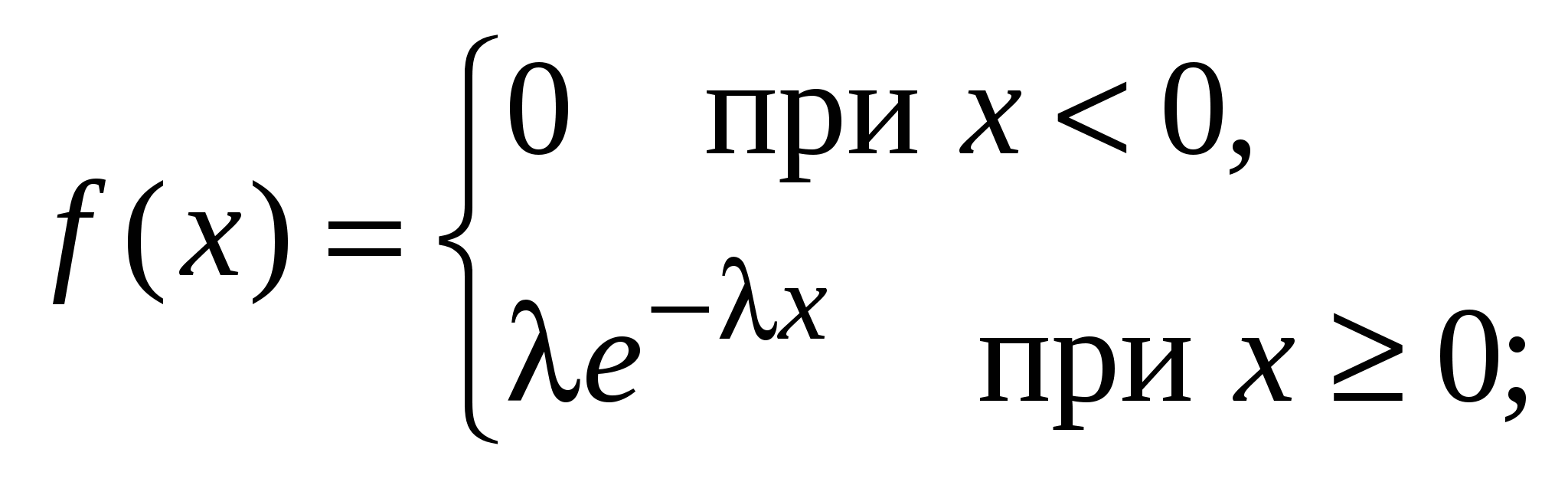
M[X] = D[X] = .
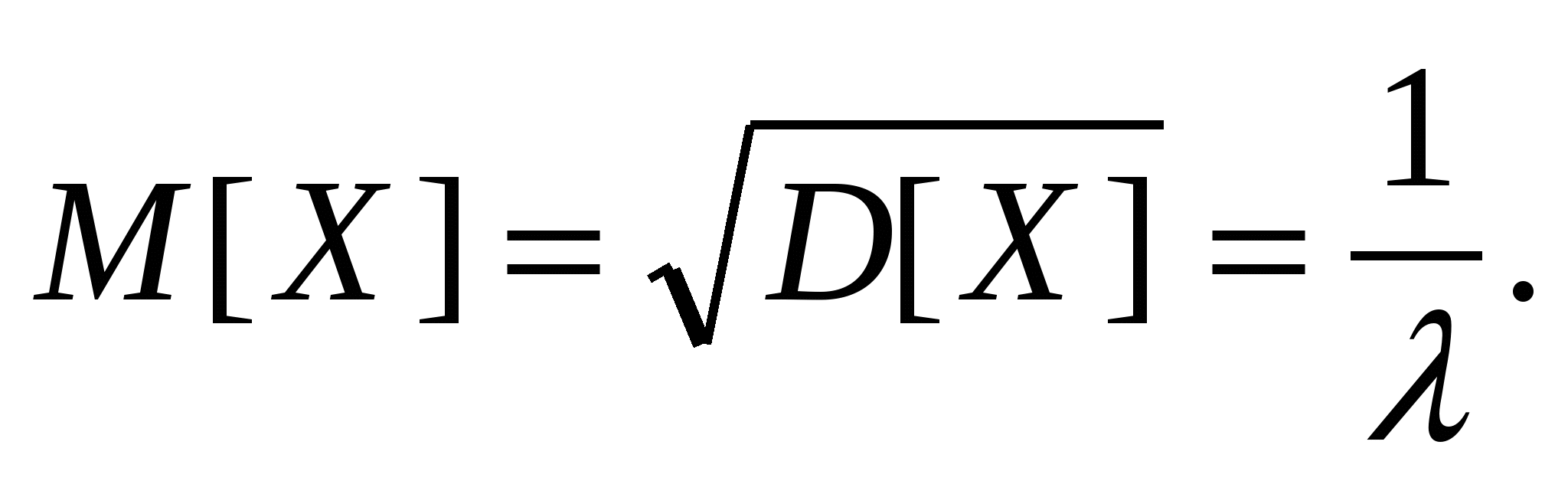
	Нормальное распределение (рис. 3):
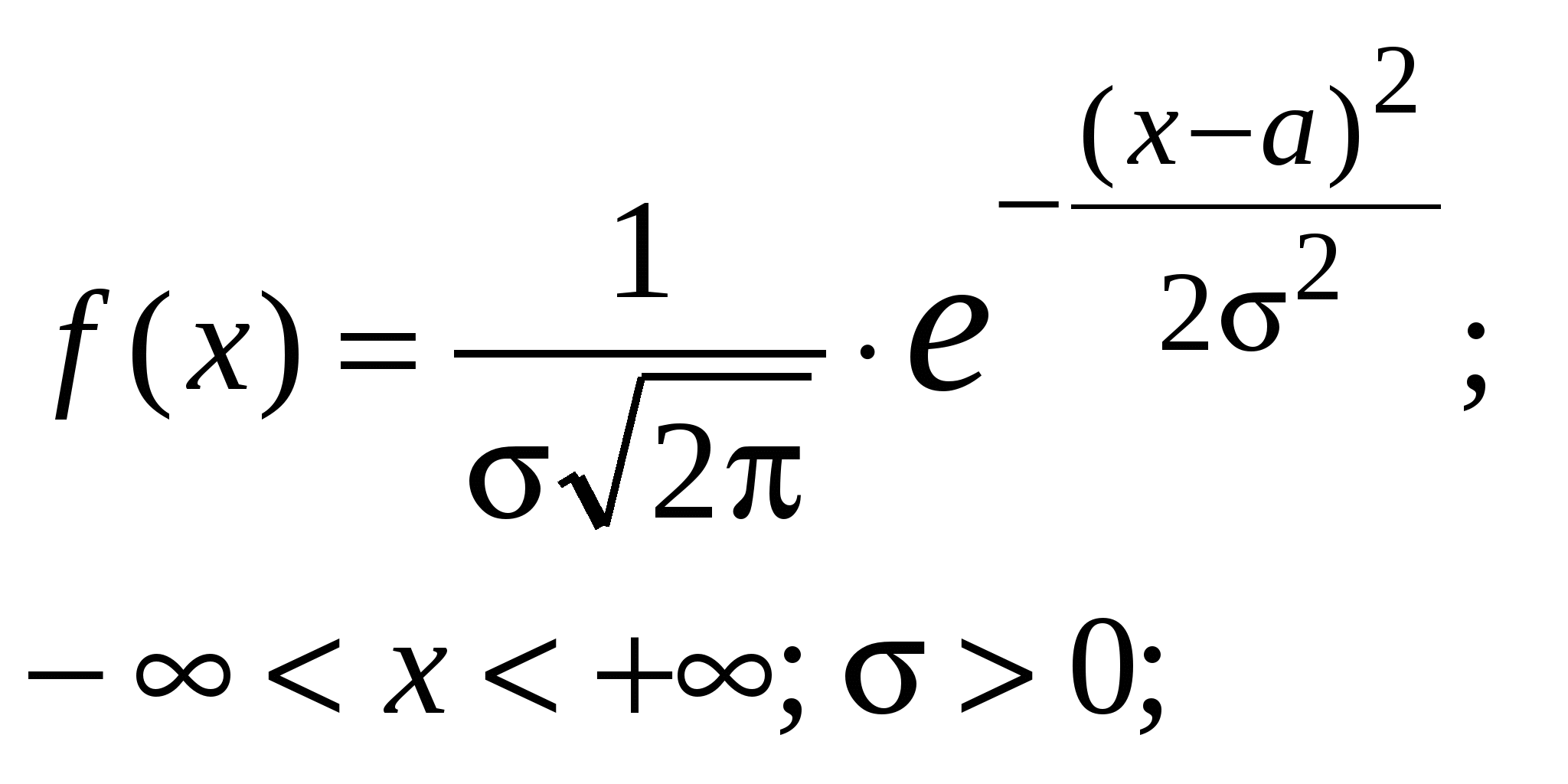
	M[X] = a, D[X] = 2.

Рис. 1	Рис. 2	Рис. 3