3. Случайные векторы
Дискретный случайный вектор
|
Непрерывный случайный вектор
|
3.1. Законы распределения
|
Функция распределения:
|
F(x, y) = P(X < x; Y < y);
F(–, y) = F(x, –) = F(–, –) = 0;
F(+, +) = 1;
F(x, +) = Fx(x); F(+, y) = Fy(y);
F(x, y) – неубывающая по x и y.
|
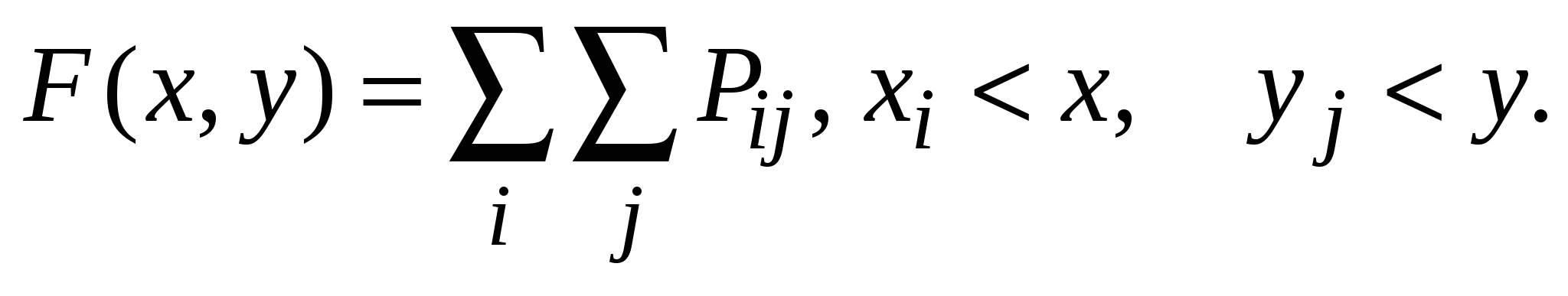
|
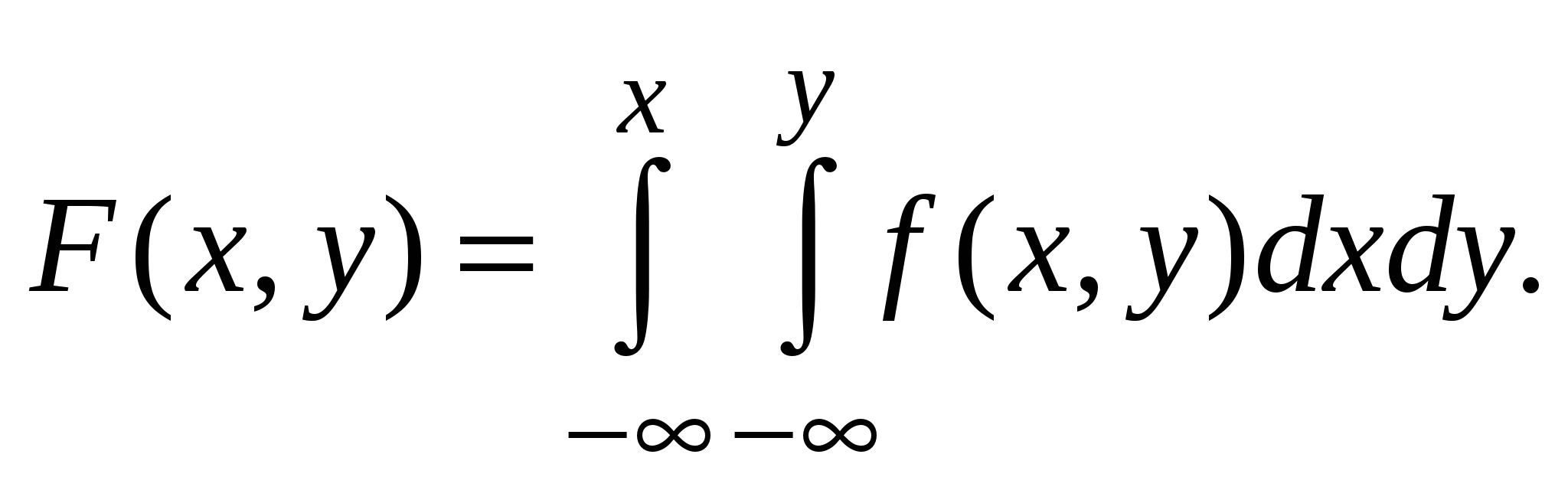
|
Таблица распределения
|
Плотность распределения:
|
X Y Y
|
y1 … yj … ym
|
x1
|
p11 … p1j … p1m
|
…
|
………………….
|
xi
|
pi1 … pij … pim
|
…
|
………………….
|
xn
|
pn1 … pnj … pnm
|
|
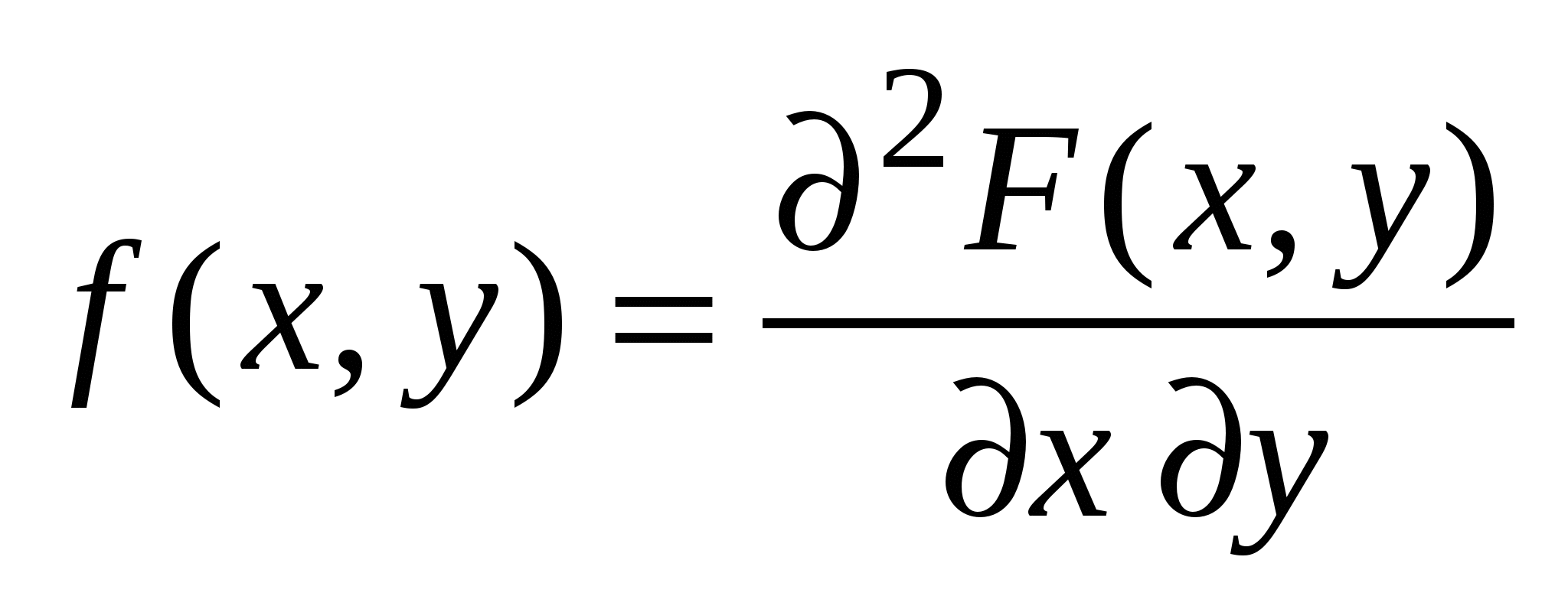 ; ;
|
Pij 0;
|
F(x, y) 0;
|
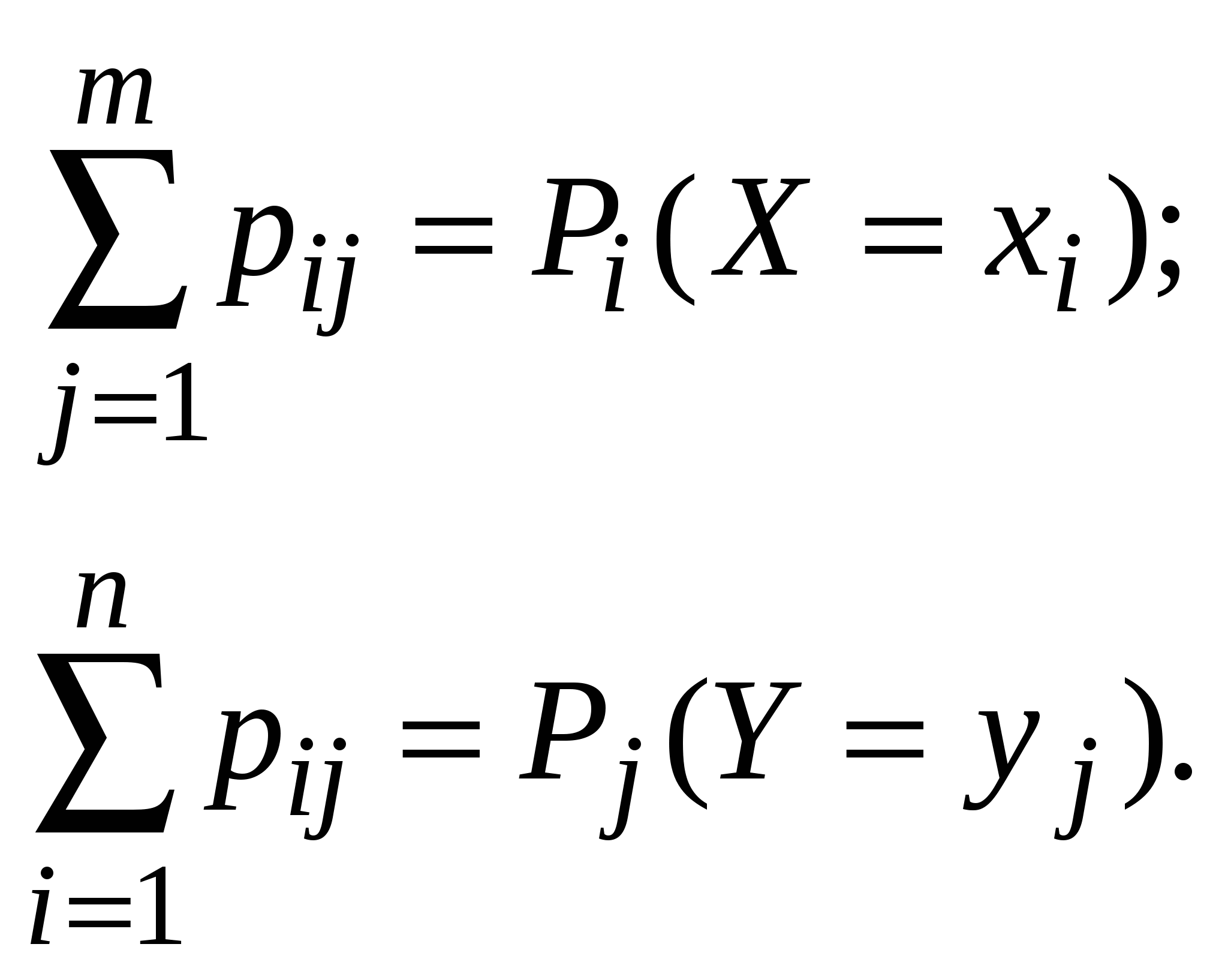
|
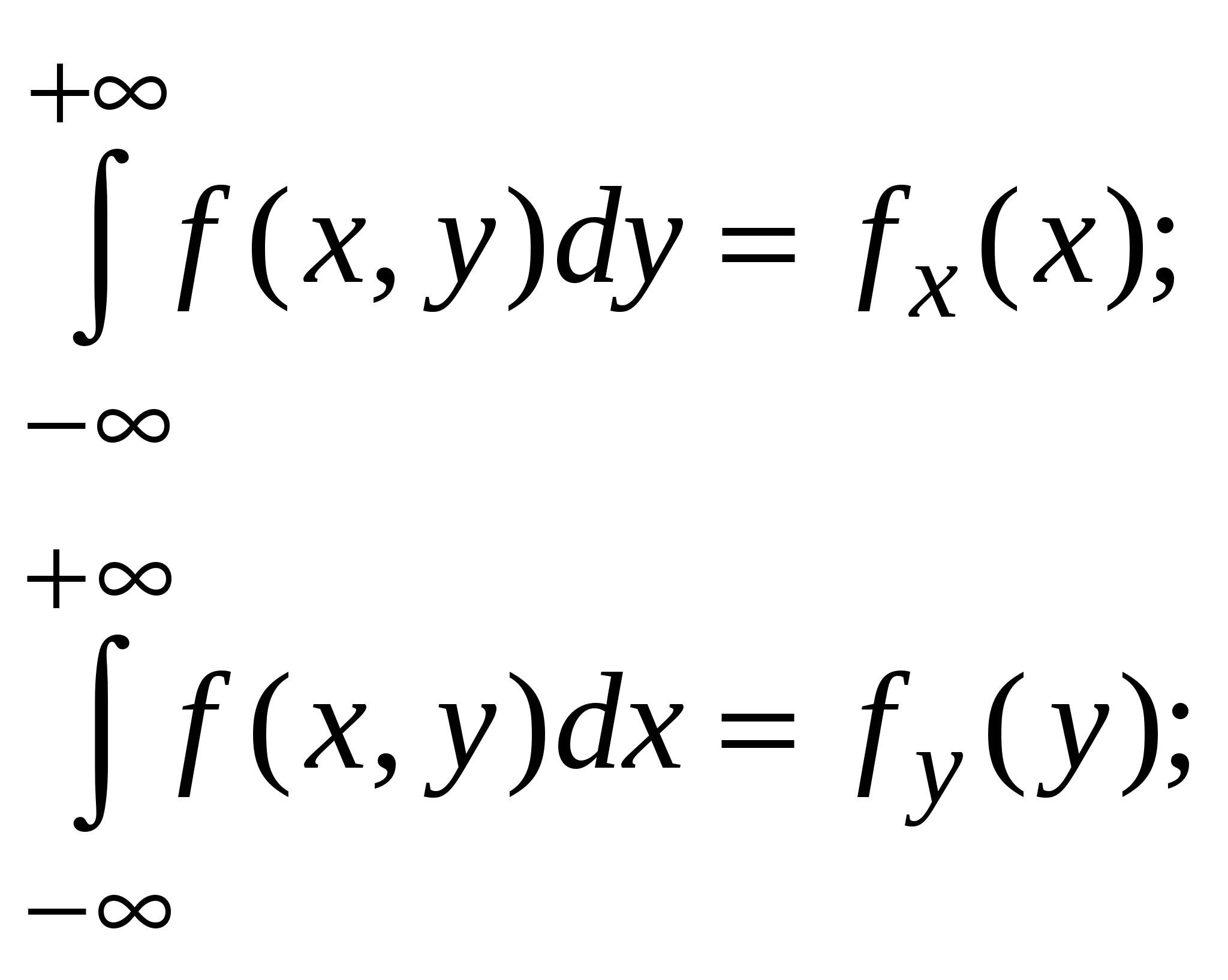
|
Условие нормировки:
|
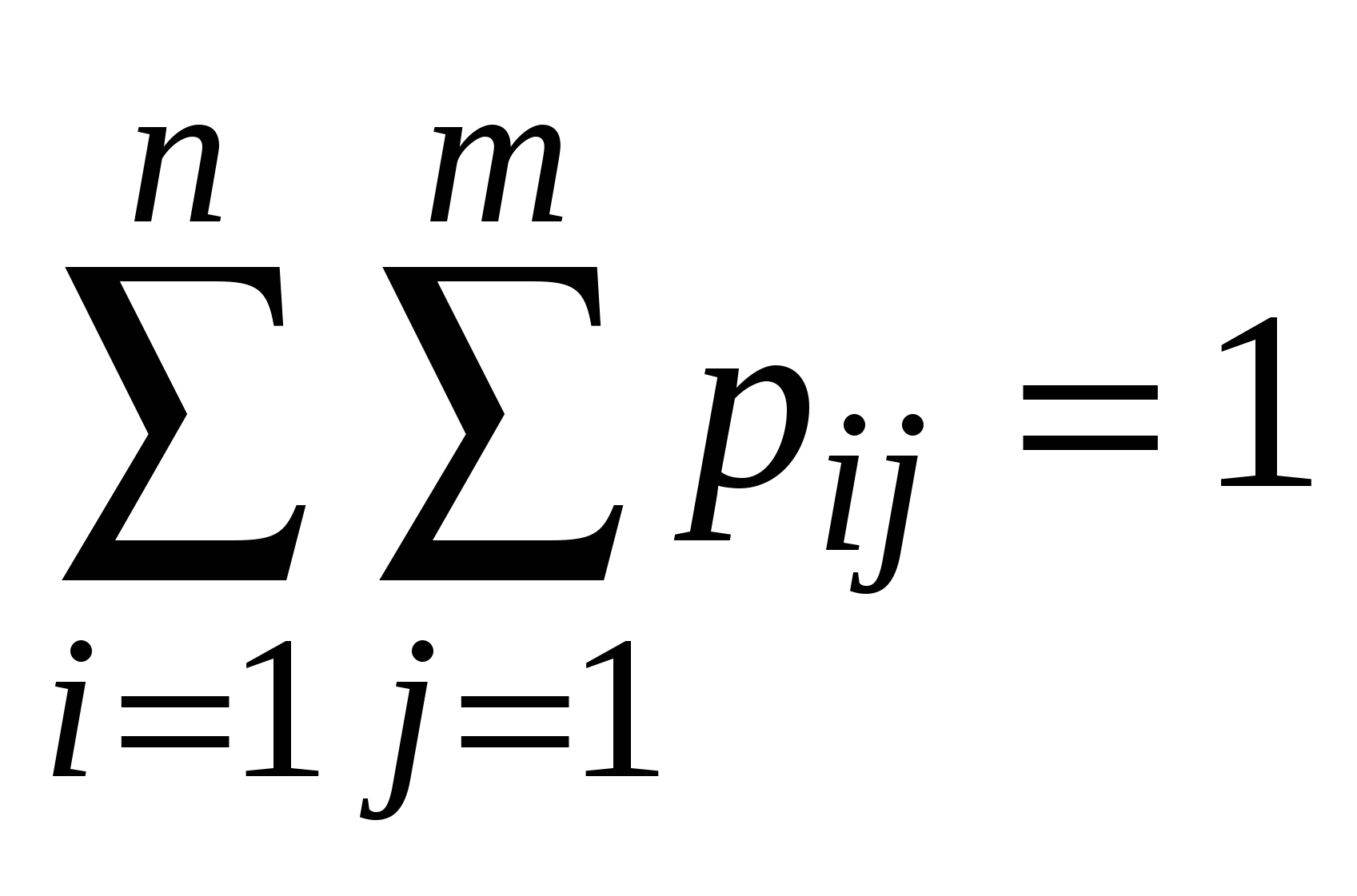 . .
|
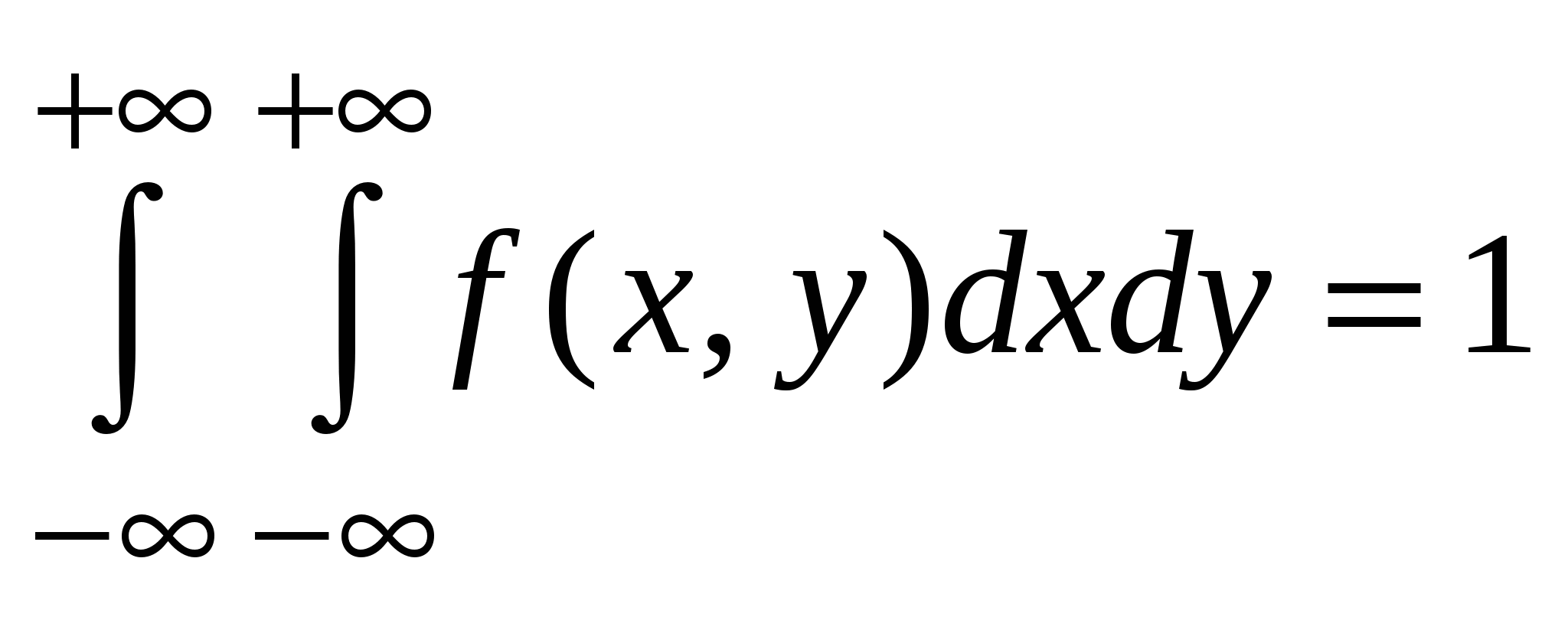 . .
|
Дискретный случайный вектор
|
Непрерывный случайный вектор
|
3.2. Числовые характеристики
|
Математическое ожидание:
|
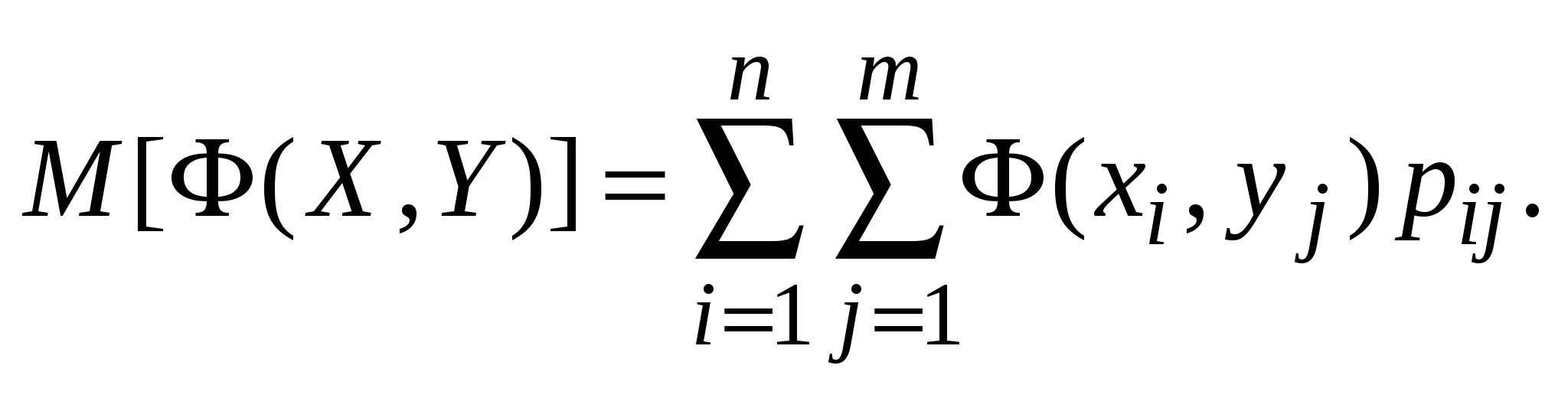
|
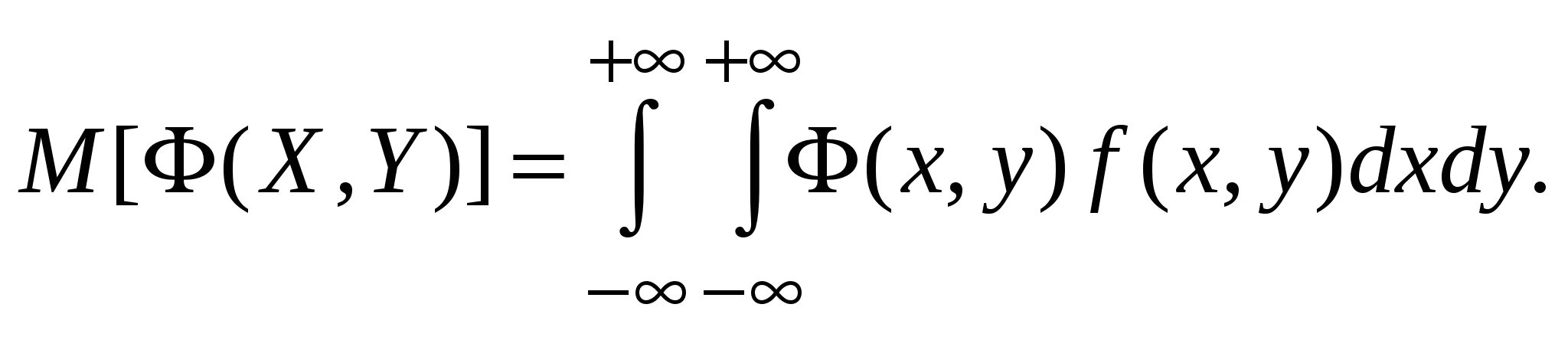
|
Дисперсия:
D[X] = M[(X – M[X])2] = M[X2] – (M[X])2.
Корреляционный момент:
K[X,Y] = M[(X – M[X]) (Y – M[Y])] = M[X Y] – M[X] M[Y].
|
Коэффициент корреляции:
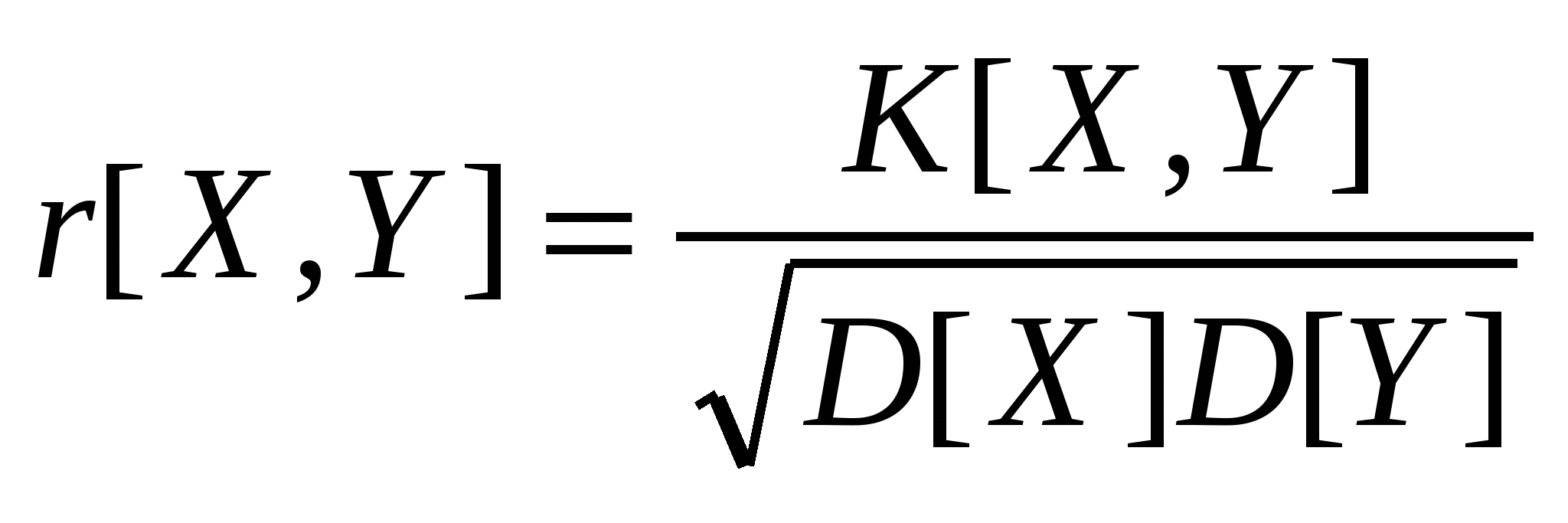 . .
|
3.3. Независимые случайные величины
|
Условия независимости:
F(x,y) = Fx(x) Fy(y);
|
Pij = Pi Pj.
|
f(x,y) = fx(x) fy(y).
|
Свойства числовых характеристик:
|
M[X Y] = M[X] M[Y];
D[X + Y] = D[X] + D[Y];
K[X,Y] = 0, r[X,Y] = 0.
|
3.4. Зависимые случайные величины
|
Условные законы распределения:
|
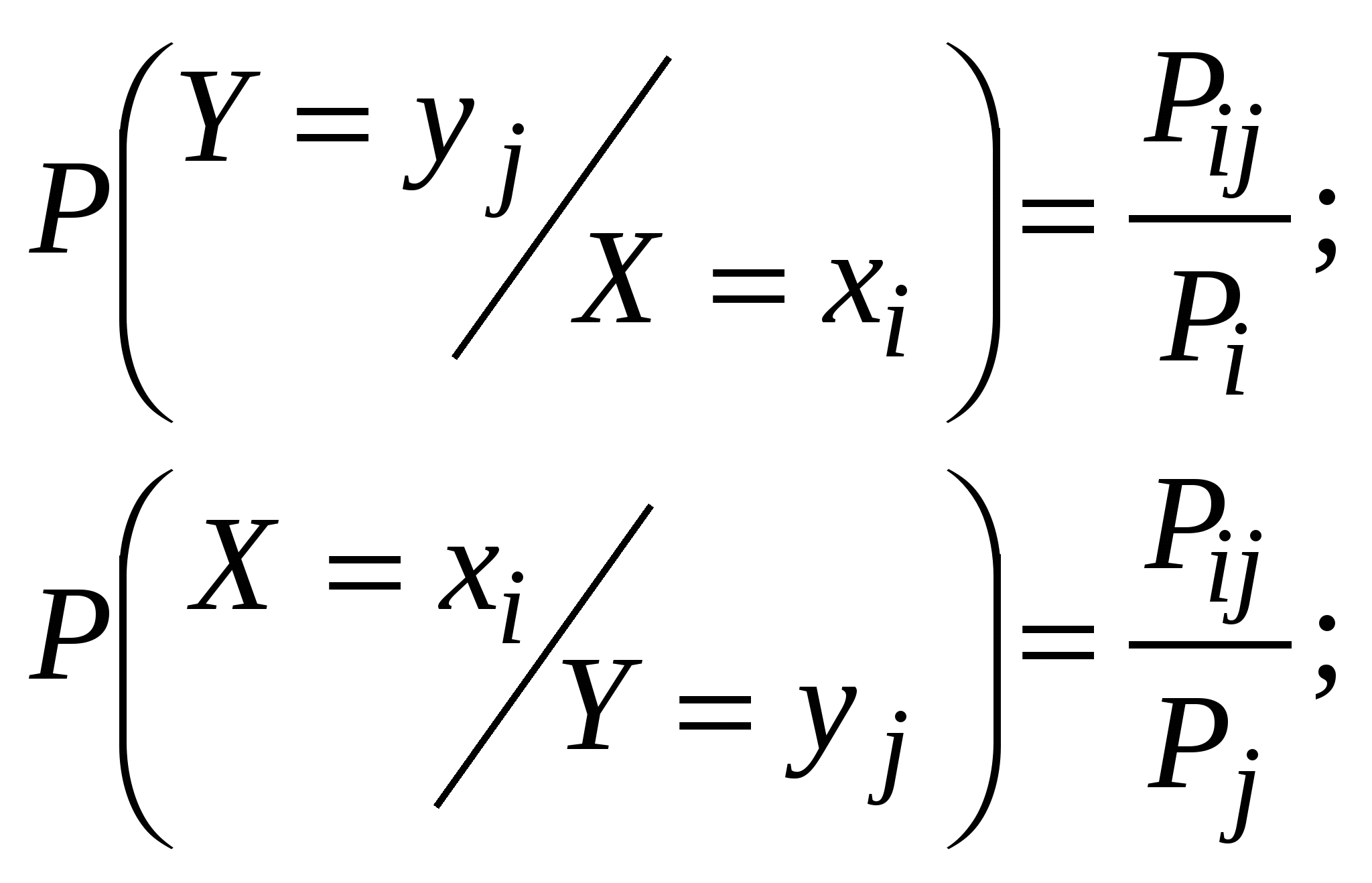
|
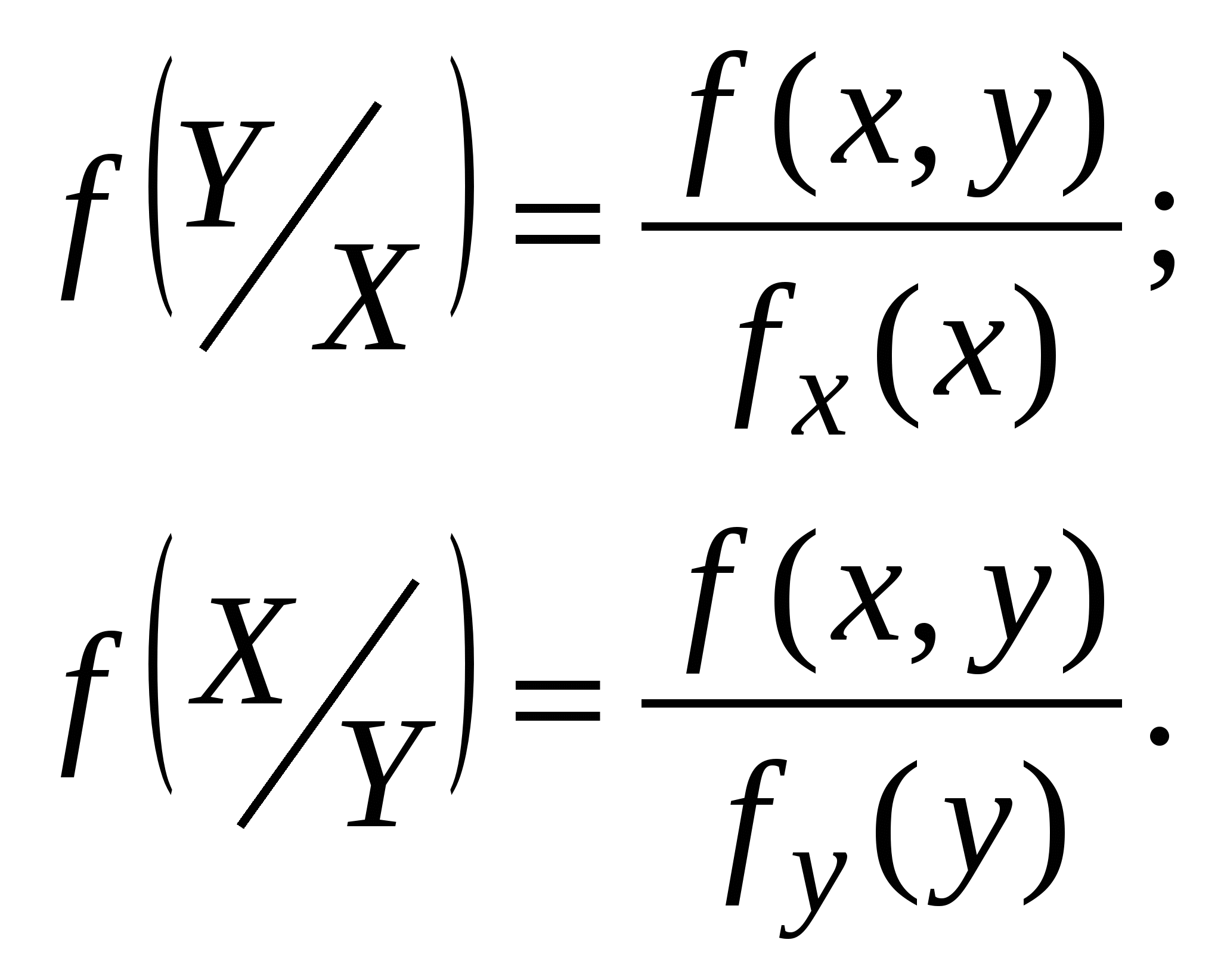
|
Условные математические ожидания:
|

|
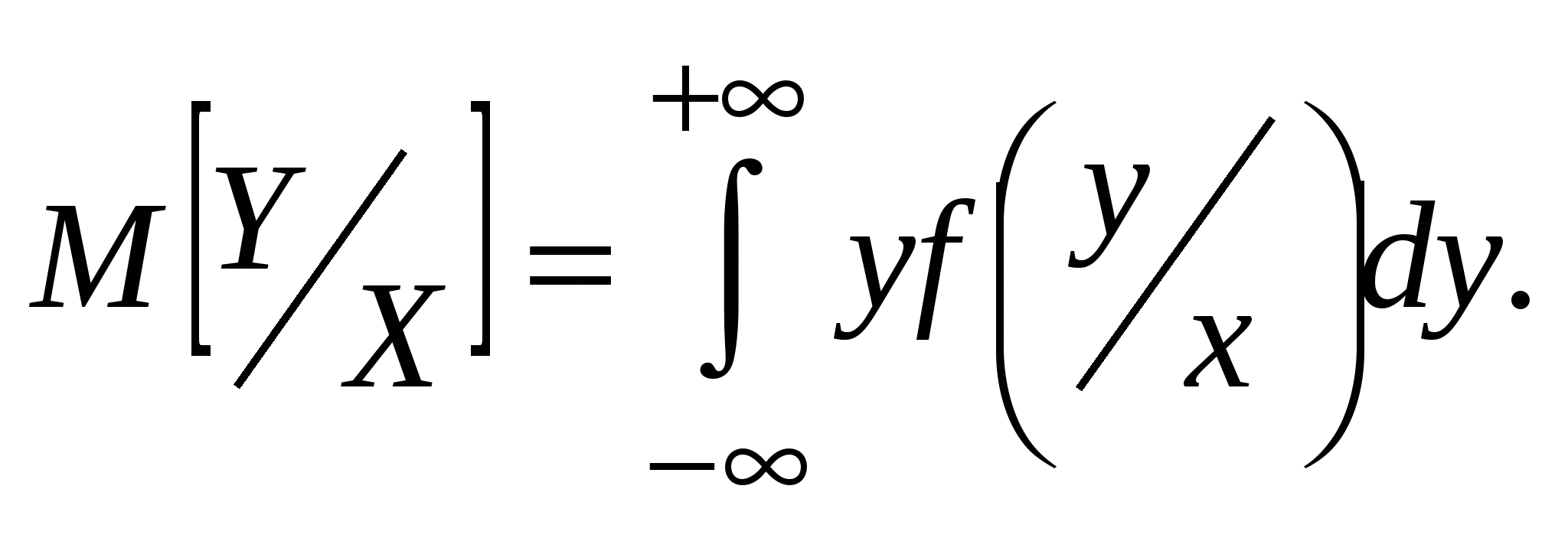
|
3.3. Свойства числовых характеристик
|
Математическое ожидание:
xmin M[X] xmax;
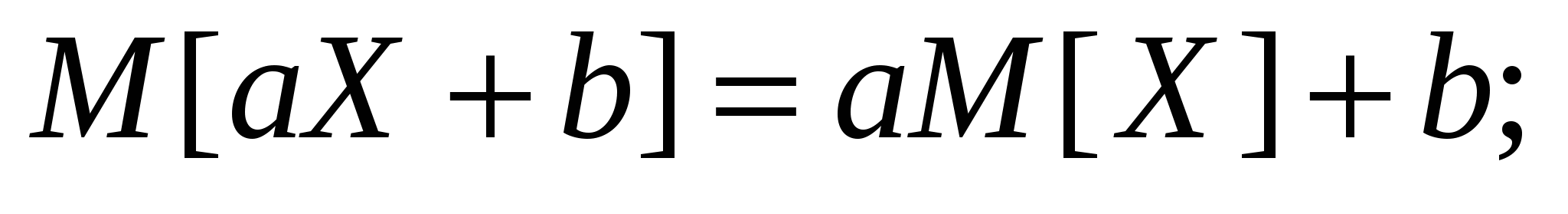
M[X + Y] = M[X] + M[Y];
M[X Y] = M[X] M[Y] + K[X,Y].
|
Дисперсия:
D[X] 0;
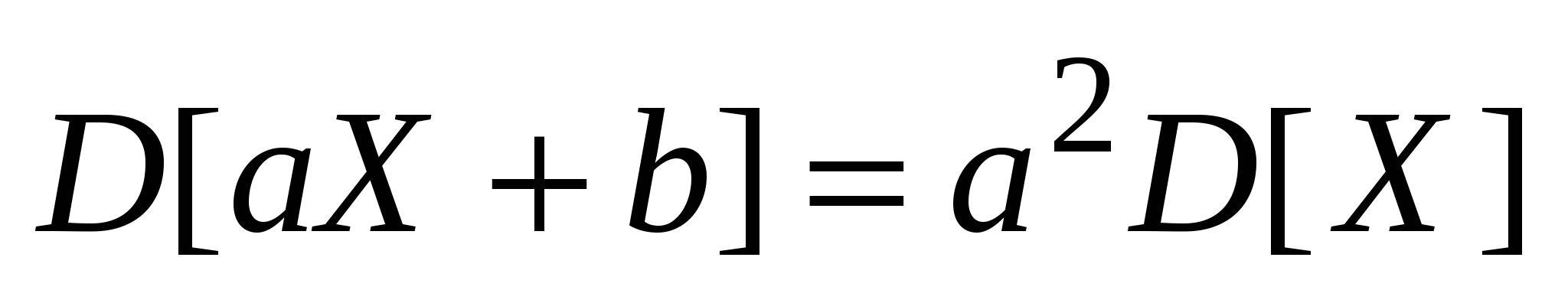 ; ;
D[X + Y] = D[X] + D[Y] + 2K[X,Y];
D[X] = K[X,X].
|
Корреляционный момент:
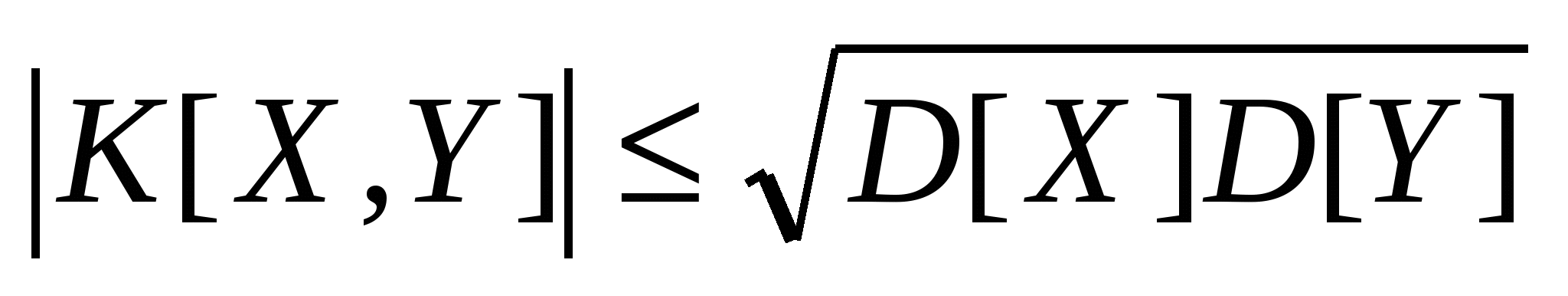 ; ;
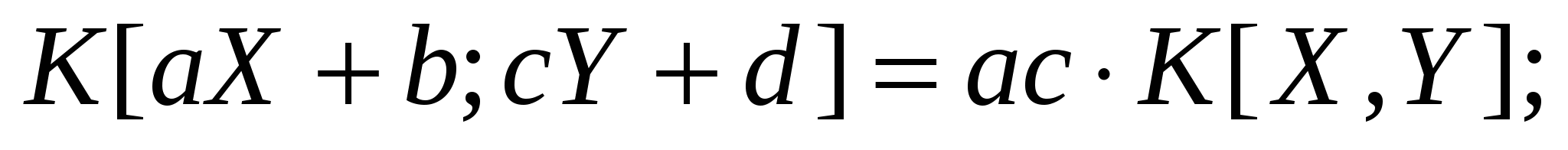
K[X,Y] = K[Y, X];
K[Y,Y] = D[Y].
|
Коэффициент корреляции:
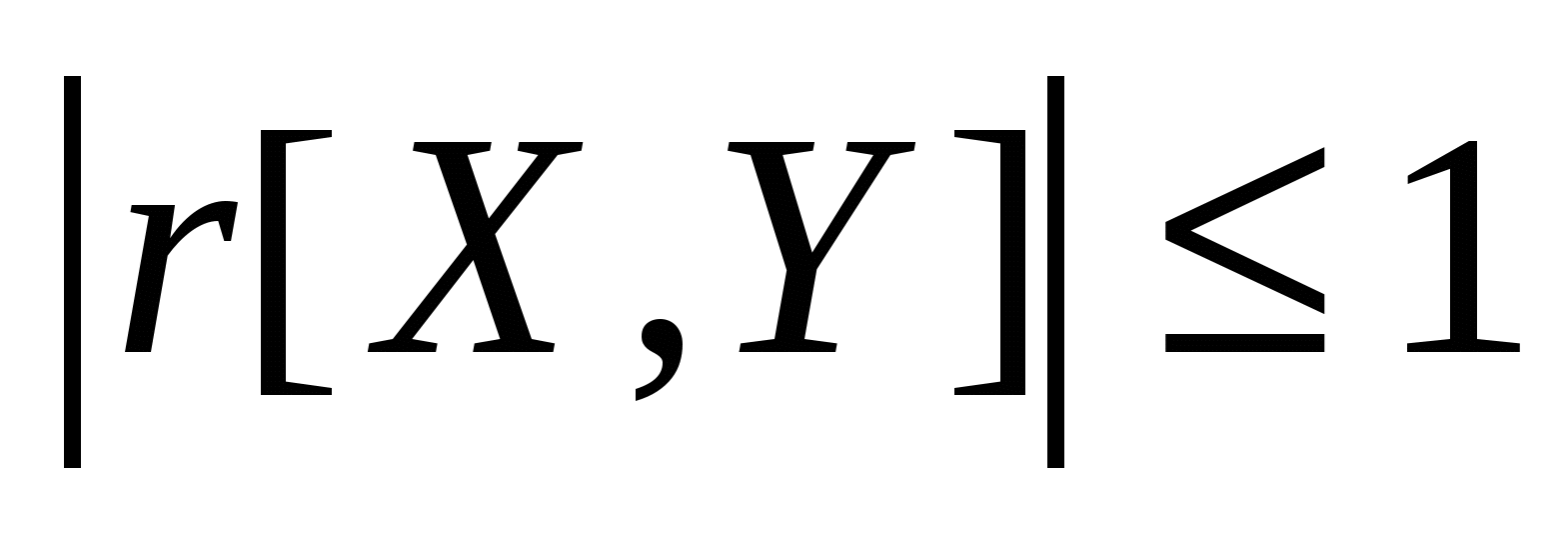 ; ;
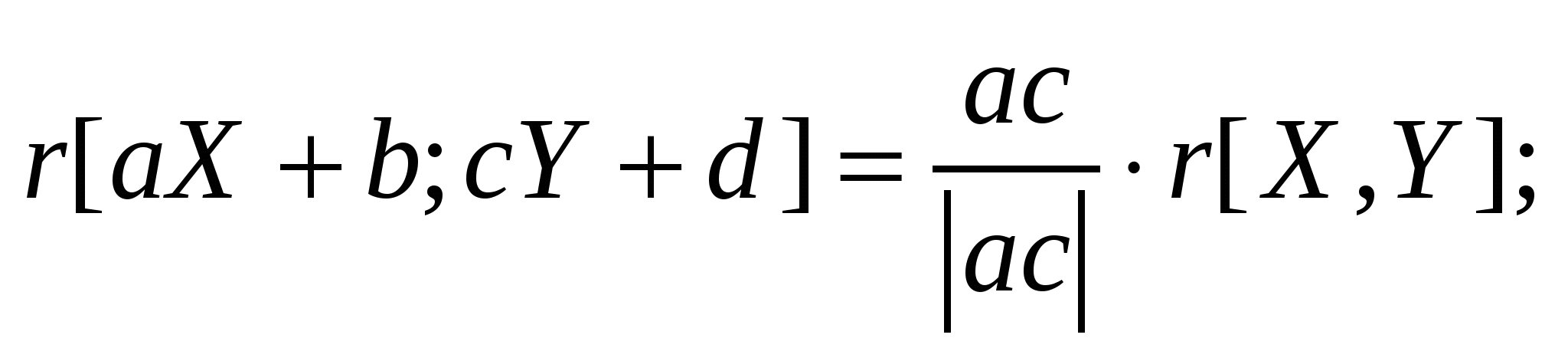
r[X,Y] = r[Y, X];
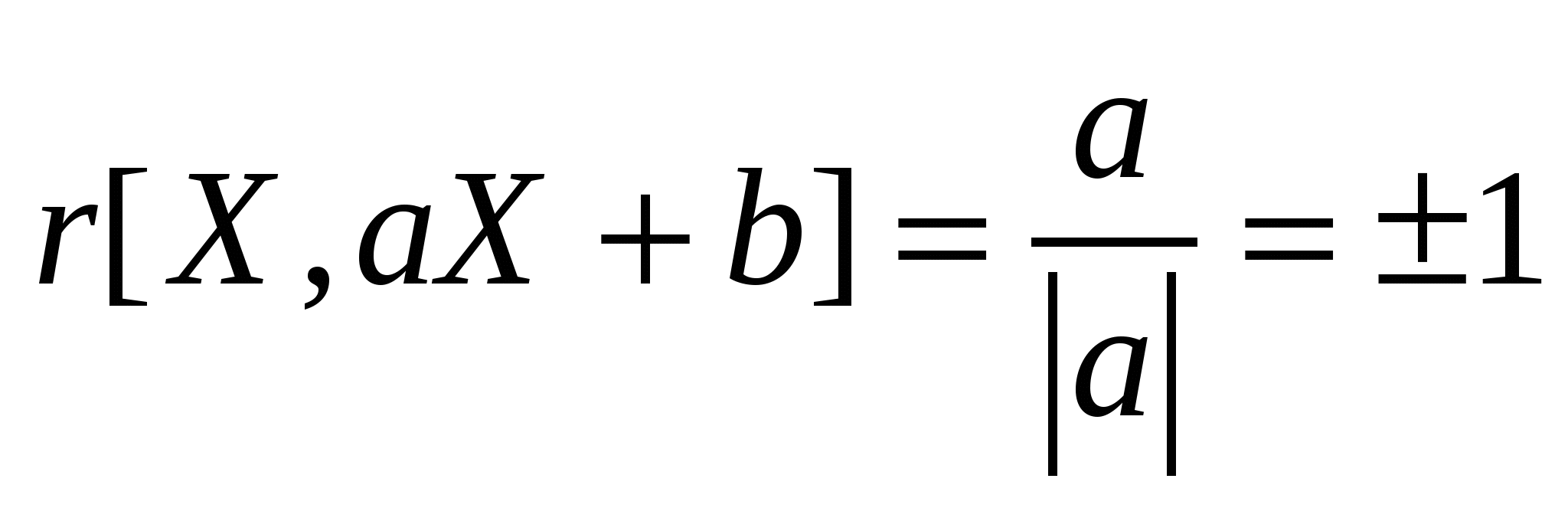 . .
|
|
 Скачать 0.85 Mb.
Скачать 0.85 Mb.