Вечернего и заочного обучения

• Название: Вечернего и заочного обучения
• Анкор: DE2AAC829C40403EA2B1245CEFB6E2D1.doc
• Дата: 21.07.2018
• Размер: 0.85 Mb.
• Имя файла: DE2AAC829C40403EA2B1245CEFB6E2D1.doc
• Тип: Контрольная работа; #21800
• страница: 1 из 8

ВЫСШАЯ МАТЕМАТИКА. Теория вероятностей и дискретная математика: методические рекомендации. Ч. 4. / ГОУВПО СПбГУТ. – СПб, 2007. Полевая Г.М., Стукалова В.С., Дмитриева О.М.

Получено с www.vizo.ru

ФАКУЛЬТЕТ

ВЕЧЕРНЕГО И ЗАОЧНОГО ОБУЧЕНИЯ
Г.М. Полевая

В.С. Стукалова

О.М. Дмитриева


ВЫСШАЯ МАТЕМАТИКА
ТЕОРИЯ ВЕРЯТНОСТЕЙ

И ДИСКРЕТНАЯ МАТЕМАТИКА
Часть 4

Теория вероятностей 3

Программа дисциплины 3

Теоретический материал 5

1. Случайные события 5

2. Случайные величины 7

3. Случайные векторы 10

Контрольная работа 10

Решение типовых задач 14

Случайные события 14

Случайные величины 20

Дискретная математика 26

Программа дисциплины 26

Теоретический материал 27

Классы функций 27

Логические функции двух переменных f(x1, x2) 24

Свойства логических функций 25

Полиномы Жегалкина 25

Контрольная работа 26

Задание 1 26

Задание 2 26

Задание 3 26

Решение типовых задач 28

ЛИТЕРАТУРА 33

Теория вероятностей

Программа дисциплины

1. 
   Комбинаторика.
   
2. 
   Элементарные и составные события. Алгебра событий.
   
3. 
   Классическое определение вероятности.
   
4. 
   Вероятность суммы событий.
   
5. 
   Условная вероятность. Вероятность произведения.
   
6. 
   Формула полной вероятности.
   
7. 
   Формула Байеса.
   
8. 
   Формула Бернулли.
   
9. 
   Формула Пуассона.
   
10. 
    Случайные величины.
    
11. 
    Функция распределения случайных величин.
    
12. 
    Дискретные случайные величины (ДСВ), ряд распределения.
    
13. 
    Числовые характеристики ДСВ. Свойства.
    
14. 
    Биноминальное распределение.
    
15. 
    Распределение Пуассона.
    
16. 
    Непрерывные случайные величины, плотность распределения случайных величин, числовые характеристики.
    
17. 
    Равномерное распределение.
    
18. 
    Показательное распределение.
    
19. 
    Нормальный закон распределения.
    
20. 
    Системы двух случайных величин. Функция распределения, ее свойства.
    
21. 
    Система двух дискретных случайных величин.
    
22. 
    Числовые характеристики системы ДСВ. Корреляционный момент. Коэффициент корреляции.
    
23. 
    Зависимые и независимые случайные величины. Условные законы распределения. Линия регрессии.
    
24. 
    Связь независимости и некоррелированности.
    
25. 
    Непрерывный случайный вектор. Законы распределения.
    
26. 
    Числовые характеристики непрерывного случайного вектора.
    

Теоретический материал

1. Случайные события

1.1. Классическое определение вероятности события:

	А – событие;
	m – число исходов, благоприятных А;
	n – число всех исходов.

1.2. Вероятность суммы событий:

а) для совместных P(A + B) = P(A) + P(B) – P(AB);

б) для несовместных P(A + B) = P(A) + P(B).

1.3. Условная вероятность: .

Вероятность произведения: .

Условие независимости событий: P(A  B) = P(A)  P(B).

1.4. Формула полной вероятности:

где H₁,..., H_n – полная группа попарно несовместных событий;

Формула Байеса: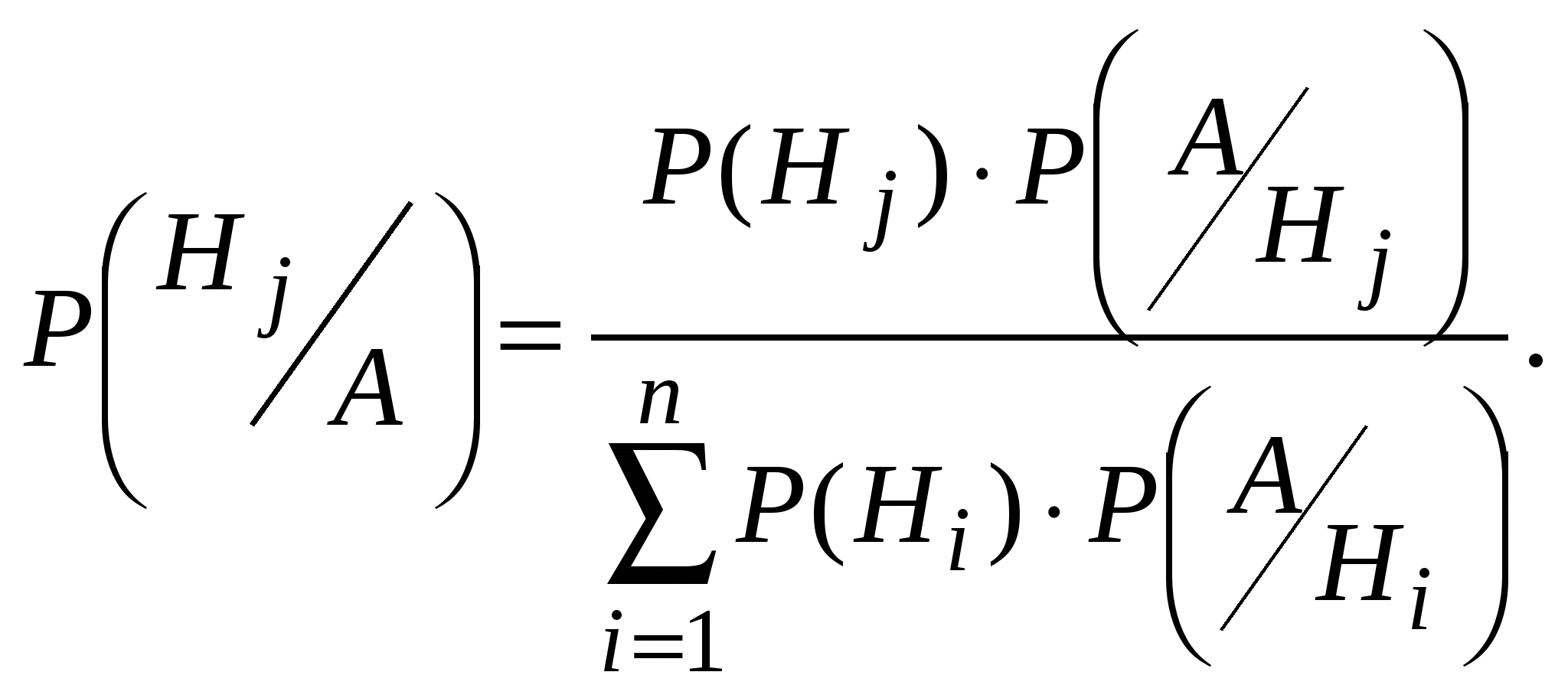

1.5. Формула Бернулли:

1.6. Формула Пуассона: