Вечернего и заочного обучения

• Название: Вечернего и заочного обучения
• Анкор: DE2AAC829C40403EA2B1245CEFB6E2D1.doc
• Дата: 21.07.2018
• Размер: 0.85 Mb.
• Имя файла: DE2AAC829C40403EA2B1245CEFB6E2D1.doc
• Тип: Контрольная работа; #21800
• страница: 8 из 8

№ п/п	Свойства логических функций
1		x + x = 0
2
3		x + y = y + x
4	x (y z) = (x y) z	x + (y + z) = (x + y) + z
5	x  (y  z) = (x  y)  z	x (y + z) = x y + x z
6	x  y = y  x; x  y = y  x	x  y = y  x
7	x (y  z) = x y  x z	x  y = y  x
8	x  (y z) = (x  y)(x  z)	x  y = y  x
9		(x  y)  z = x  (y  z)
10	x  xy = x	x  x = 1
11		x  x = x  x =
12
13
№ п/п	Полиномы Жегалкина
1
2
3
4
5
6

Контрольная работа

1. Записать в двоичной системе номер зачетной книжки, приписать в конце единицы до получения 16 разрядов.

Получаетсяf₀(x₁, x₂, x₃, x₄).

2. Первые 8 разрядов f₀ образуют функцию f₁(x₁, x₂, x₃).

3. Последние 8 разрядов f₀ образуют функцию f₂(x₁, x₂, x₃), причем, если f₂ = 1 только на двух наборах (x₁, x₂, x₃), то положить f₂(0, 0, 0) = 1.

Задание 1

1. По таблице истинности f₁(x₁, x₂, x₃), f₂(x₁, x₂, x₃) составить СДНФ и упростить ее (если возможно), обозначив результаты D₁, D₂.

2. Составить таблицу истинности для f*₁. Используя принцип двойственности, получить формулу D*₂.

3. Используя правило де Моргана, получить КНФ для D₁ и D₂.

4. По таблице истинности f₁,f₂ составить СКНФ; раскрывая скобки и упрощая, получить ДНФ.

Задание 2

1. Для f₂(x₁, x₂, x₃), f₀(x₁, x₂, x₃, x₄) с помощью карт Карно найти сокращенную ДНФ и сокращенную КНФ.

2. Нарисовать П-схему.

3. Составить таблицу Поста и выделить базисы из набора функций: f₁(x₁, x₂, x₃);f₂(x₁, x₂, x₃); f₃(x₁, x₂, x₃) = x₁x₂  (x₂  x₃); f₄(x₁, x₂, x₃) = x₁  x₂x₃; f₅(x₁, x₂, x₃) = (x₁  x₃) x₂.

Задание 3

1. Закодировать свою фамилию простейшим кодом и кодом Хэмминга (4,7).

2. Передано слово, закодированное простейшим кодом и кодом Хэмминга (4,7).

Принято: 0100 [i] 01011001101011000110011 [j] 111100,

где i = 0,5 + (–1)^a 0,5; j = 0,5 + (–1)^b 0,5.

Какое слово передано?

Решение типовых задач

Упростить ДНФ можно, используя теоремы поглощения и Блейка. Если в ДНФ какое-нибудь слагаемое входит сомножителем в другие слагаемые, то оно их поглощает.

Пример 7. Упростить:

x  x y  x z  x = x;

x = .

Часто, чтобы применить поглощение, необходимо предварительно использовать правило Блейка. Это можно сделать в случае, если одно слагаемое содержит множитель, а другое слагаемое содержит отрицание этого множителя.

Пример 8. Упростить:





или

При применении правил де Моргана не забывать ставить дизъюнкцию в скобки.

Пример 9. Перейти от ДНФ к КНФ:

а)

Ставим над ДНФ два отрицания. Применяя правило де Моргана к нижнему отрицанию, получаем новое ДНФ, затем, применяя правило к верхнему отрицанию, получаем КНФ:



б)

Если применить к правило Блейка, нужно дописать , но оно уже есть, поэтому отбрасываем , используя формулу справа налево, получаем .

При использовании карт Карно для упрощения ДНФ надо не забывать, что объединять кругами можно только 2^k соседних единиц (т. е. 1, 2, 4, 8, 16, …); круги должны быть максимального размера; число кругов должно быть минимальным; карты Карно соединяются по кругу.

Пример 10. Составить упрощенную ДНФ (рис. 13), изобразить соответствующую П-схему.

Выписывая сомножители надо учитывать только неизменяющиеся в круге переменные, получаем .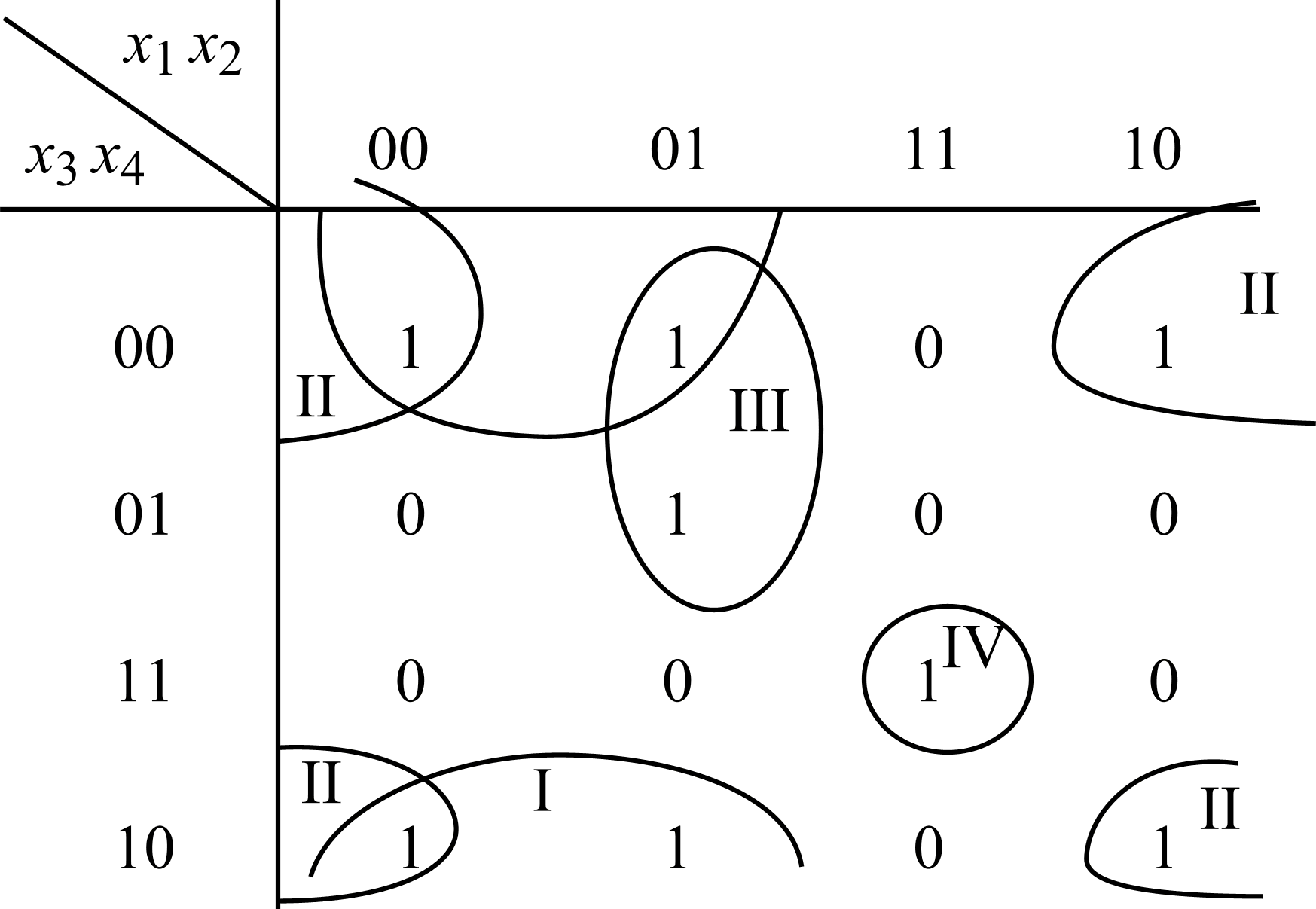



Рис. 13

Нарисуем П-схему, реализующую эту функцию. Конъюнкции отвечает последовательное соединение, а дизъюнкции параллельное (рис. 14).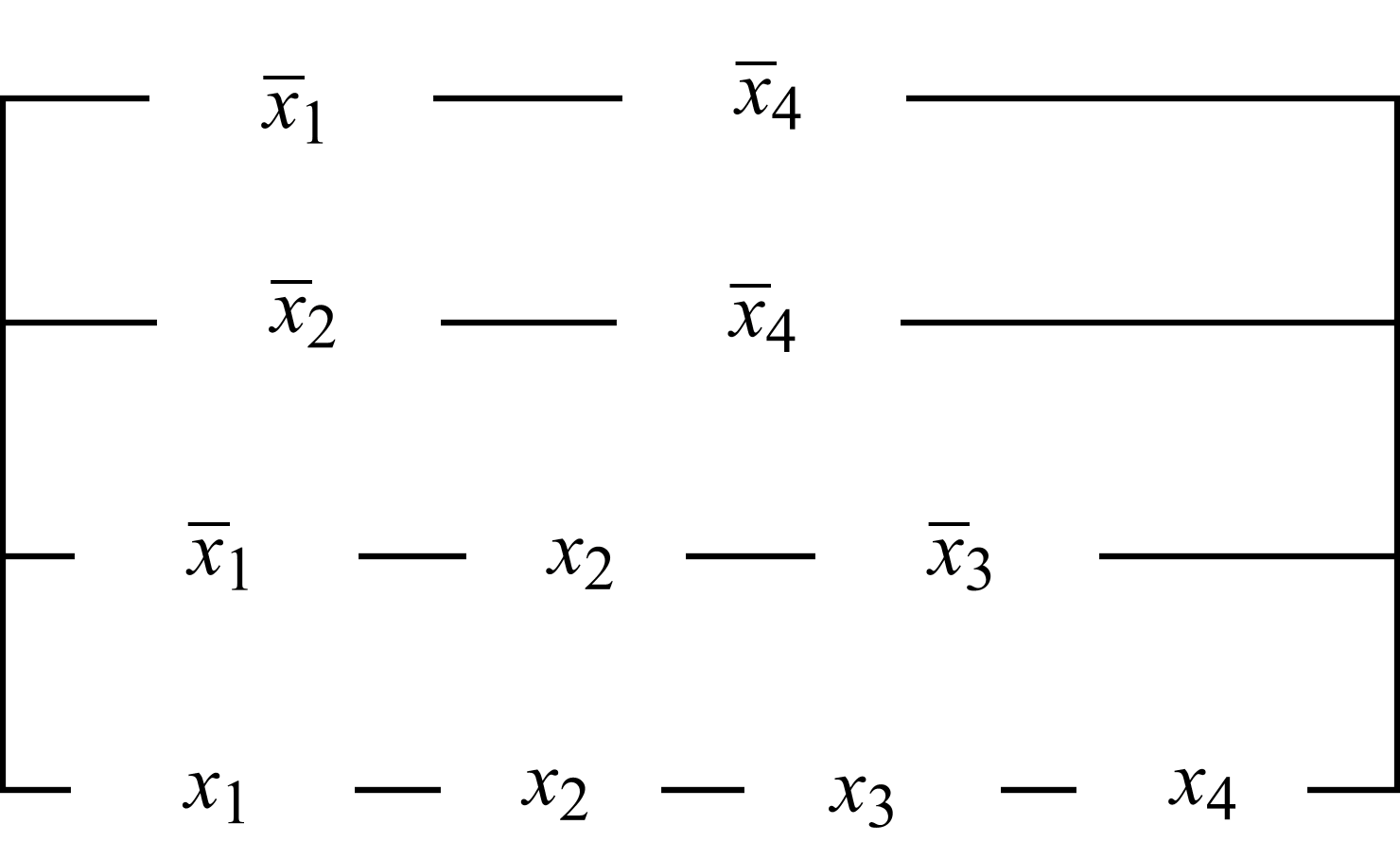



Рис. 14

Для проверки линейности функции можно использовать таблицу истинности. Если число нулей не равно числу единиц, то функция нелинейная. В случае равенства числа нулей и единиц надо построить полином Жегалкина.

Пример 11. Проверить линейность функции:

а) функция f(x, y) задана таблично.

x y	f(x, y)
00 01 10 11	1 0 0 1

Полином от двух переменных имеет вид

P(x, y) = a₀ + a₁ x + a₂ y + a₃ x y,

где коэффициенты a₀, a₁, a₂, a₃ равны 0 или 1.

Для нашей функции:

P(0,0) = a₀ = 1;

P(0,1) = a₀ + a₂ = 1+ a₂ = 0, a₂ = 1;

P(1,0) = a₀ + a₁ = 1+ a₁ =0, a₁ = 1;

P(1,1) = a₀ + a₁ + a₂ + a₃ = 1 + 1 + 1 + a₃ = 1, a₃ = 0.

Значит P(x, y) = 1 + x + y – линейная функция.

б) функция f(x, y) = (x  y)  x.

Если функция задана формулой, полином Жегалкина можно получить тождественными преобразованиями, например, в нашем случае

,

значит, функция f(x, y) нелинейная.

При построении использовали свойства x + x = 0 и .

При нахождении базисов по таблице Поста следует помнить, что базис – это минимальная полная система, поэтому проверку на полноту начинаем с наборов из одной функции, постепенно увеличивая их число. Найденные базисы не включаются в большие наборы.

Пример 12. Найти базисы по таблице Поста.

f	T0	T1	L	M	S
f1 f2 f3 f4	+ + – +	– – + +	+ – – –	– – – +	– + – –

В каждом столбце есть минус, следовательно, система полная.
Базисов из одной функции нет, так как в каждой строке есть плюс.

Проверяем наборы из двух функций на полноту:
{f₁, f₃} – базис, {f₂, f₃} – базис, других базисов нет.

ЛИТЕРАТУРА

1. Пискунов, Н.С. Дифференциальное и интегральное исчисление. – М.: Наука, 1995. – Т.

2. Кудрявцев, В.А. Краткий курс высшей математики / В.А. Кудрявцев, Б.П. Демидович. – М.: Наука, 1989.

3. Данко, П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Л. Кожевникова. – М.: Высшая математика, 1980. – Ч.2.