Главная страница
Навигация по странице:

  • Длина вектора Определение.

  • Нулевой вектор Определение.

  • Коллинеарные вектора Определение.

  • Условия коллинеарности векторов Два вектора будут коллинеарны при выполнении любого из этих условий: Условие коллинеарности векторов 1.

  • Противоположно направленные вектора Определение.

  • Компланарные вектора Определение.

  • Условия компланарности векторов Для 3-х векторов.

  • Равные вектора Определение.

  • Условие равенства векторов.

  • Единичный вектор Определение.

  • Ортогональность векторов

  • Условие ортогональности векторов.

  • Определение.

  • Основное соотношение.

  • Геометрическая интерпретация.

  • Алгебраическая интерпретация.

    		•

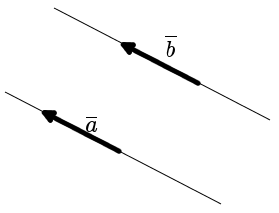
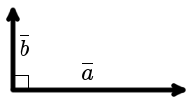
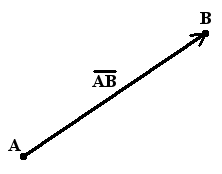
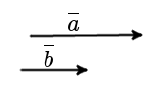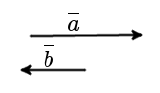    векторы. Вектор это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало точка


    Скачать 276.13 Kb.
    НазваниеВектор это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало точка
    Дата30.12.2022
    Размер276.13 Kb.
    Формат файлаdocx
    Имя файлавекторы.docx
    ТипДокументы
    #869271


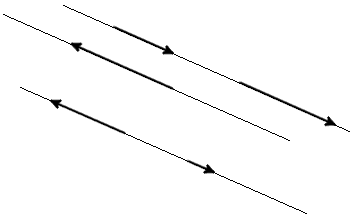
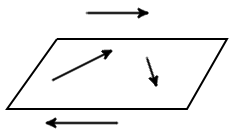
    Вектор - это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало - точка. Модуль вектора (абсолютная величина) - длина этого направленного отрезка.

    Если начало вектора совпадает с его концом, получим нулевой вектор.

    Два вектора являются равными, если их длина одинаковая и они имеют одинаковое направление. Они совмещаются при переносе.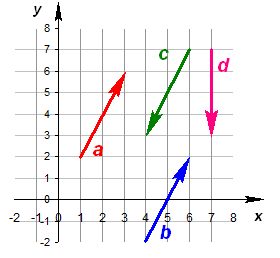



    Длина вектора

    Определение. Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.

    Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.

    Нулевой вектор

    Определение. Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.

    Нулевой вектор обычно обозначается как 0.

    Длина нулевого вектора равна нулю.

    Коллинеарные вектора

    Определение. Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 2).

    рис. 2

    Условия коллинеарности векторов

    Два вектора будут коллинеарны при выполнении любого из этих условий:

    Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что

    a = n · b

    Условия коллинеарности векторов 2. Два вектора коллинеарны, если отношения их координат равны.

    N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.

    Условия коллинеарности векторов 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.

    N.B. Условие 3 применимо только для трехмерных (пространственных) задач.

    Сонаправленные вектора

    Определение. Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b (рис. 3).

    рис. 3

    Противоположно направленные вектора

    Определение. Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b (рис. 4).

    рис. 4

    Компланарные вектора

    Определение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).

    рис. 5

    Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.

    Условия компланарности векторов

    • Для 3-х векторов. Три вектора компланарны если их смешанное произведение равно нулю.

    • Для 3-х векторов. Три вектора компланарны если они линейно зависимы.

    • Для n векторов. Вектора компланарны если среди них не более двух линейно независимых векторов.

    Равные вектора

    Определение. Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).




    рис. 6




    Условие равенства векторов. Вектора равны, если их координаты равны.
    То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

    a = b, если a↑↑b и |a| = |b|.

    Определение.'>Единичный вектор

    Определение. Единичным вектором или ортом - называется вектор, длина которого равна единице.

    Основное соотношение.Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.

    Ортогональность векторов

    Определение.

     Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1). 

    рис. 1

    Условие ортогональности векторов.Два вектора a и b ортогональны (перпендикулярны), если их скалярное произведение равно нулю.

    a · b = 0

    Формулы определения координат вектора заданного координатами его начальной и конечной точки

    Формула определения координат вектора для плоских задач


    В случае плоской задачи вектор AB заданный координатами точек A(Ax ; Ay) и B(Bx ; By) можно найти воспользовавшись следующей формулой

    AB = {Bx - Ax ; By - Ay}

    Формула определения координат вектора для пространственных задач


    В случае пространственной задачи вектор AB заданный координатами точек A(Ax ; Ay ; Az) и B(Bx ; By ; Bz) можно найти воспользовавшись следующей формулой

    AB = {Bx - Ax ; By - Ay ; Bz - Az}

    Формула определения координат вектора для n -мерного пространства


    В случае n-мерного пространства вектор AB заданный координатами точек A(A1 ; A2 ; ... ; An) и B(B1 ; B2 ; ... ; Bn) можно найти воспользовавшись следующей формулой

    AB = {B1 - A1 ; B2 - A2 ; ... ; Bn - An}

    Определение длины вектора


    Определение.

     Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.

    Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.

    Основное соотношение. Длина вектора |a| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.

    Формулы длины вектора

    Формула длины вектора для плоских задач


    В случае плоской задачи модуль вектора a = {ax ; ay} можно найти воспользовавшись следующей формулой:

    |a| = √ax2 + ay2

    Формула длины вектора для пространственных задач


    В случае пространственной задачи модуль вектора a = {ax ; ay ; az} можно найти воспользовавшись следующей формулой:

    |a| = √ax2 + ay2 + az2



    Формулы скалярного произведения векторов заданных координатами

    Формула скалярного произведения векторов для плоских задач


    В случае плоской задачи скалярное произведение векторов a = {ax ; ay} и b = {bx ; by} можно найти воспользовавшись следующей формулой:

    a · b = ax · bx + ay · by

    Формула скалярного произведения векторов для пространственных задач


    В случае пространственной задачи скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти воспользовавшись следующей формулой:

    a · b = ax · bx + ay · by + az · bz

    Формула скалярного произведения n -мерных векторов


    В случае n-мерного пространства скалярное произведение векторов a = {a1 ; a2 ; ... ; an} и b = {b1 ; b2 ; ... ; bn} можно найти воспользовавшись следующей формулой:

    a · b = a1 · b1 + a2 · b2 + ... + an · bn



    Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:

    a · b = |a| · |b| cos α

    Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.

    написать администратору сайта