Вектор
 Скачать 107.68 Kb. Скачать 107.68 Kb.
|
|
Вектор — направленный отрезок прямой, имеющий определенную длину Длинна вектора(модуль) – называется неотрицательное число, равное расстоянию между его началом и концом Нулевой вектор – если начало и конец вектора совпадает, не имеет направленности, а его модуль равен 0 Нормальный вектор прямой - это любой ненулевой вектор, лежащий на любой прямой перпендикулярной данной. Коллинеарные вектора — Два вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой Если 2 вектора коллинеарны друг другу, то их координаты пропорциональны друг другу  Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b (в противном случае-противоположнонаправленные) Равные векторы – 2 вектора называются равными если они сонаправленные имеют равные модули Свободные векторы – множества всех равных друг другу векторов( для свободного вектора точка его начала не важна) Компланарные векторы – если 3 вектора лежат в одной плоскости (определитель векторов равен нулю) Линейная комбинация - это сумма векторов, умноженных на некоторые числа. Эти векторы могут иметь разное направление. То есть, линейная комбинация - это выражение вида где Тривиальная линейная комбинация(вырожденная) – линейная комбинация, в которой все скаляры одновременно равны нулю Нетривиальная линейная комбинация(невырожденная) – линейная комбинация, где хотя бы один из скаляров не равен нулю. Конечная система векторов S называется линейно независимой, если:
Конечная система векторов S называется линейно зависимой, если:
Базис — набор n векторов в n-мерном линейном пространстве, таких, что любой вектор пространства может быть представлен в виде некоторой их линейной комбинации, при этом ни один из базисных векторов не представим в виде линейной комбинации остальных. Базис множества-любые 2 неколлинеарных или 3 некомпланарных вектора, лежащие на плоскости или в пространстве Тройка векторов называется упорядоченной, если сказано, какой вектор идет первым, вторым, третьим. Тройка векторов называется левой (правой), если поворот от одного вектора ко второму видимый с конца третьего вектора осуществляется по ходу (против) часовой стрелки. Базис называется ортогональным, если его векторы попарно-перпендикулярны друг другу. При ортогональности прямых угловые коэффициенты двух ортогональных прямых обратно пропорциональны и противоположны по знаку  Базис называется ортонормированным, если он ортогональный и его вектора единичные. Координатами вектора в заданном базисе называют координатой разложения по базисным векторам Векторное (или линейное) пространство — математическая структура, которая представляет собой набор элементов, называемых векторами, для которых определены операции сложения друг с другом и умножения на число — скаляр Аффинная система координат – с.к. на плоскости, которая задается любой парой неколлинеарных векторов, приложенной к данной общей точке. Прямоугольная система координат(декартовая) — с.к. в которой базисные вектора ортогональны друг другу. Координатами точки в заданной с.к. будем понимать координаты ее радиус-вектора(вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.), т.е. вектора, началом которого является начало с.к., а концом – данная точка Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости однозначно определяется двумя числами — полярным углом  (первой полярной координатой точки) и полярным радиусом r (второй полярной координатой точки). (первой полярной координатой точки) и полярным радиусом r (второй полярной координатой точки).  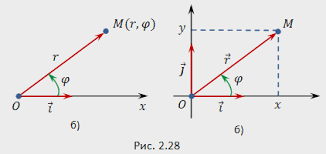 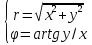 Скалярным произведением 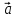  называется число равное произведению модулей этих векторов на называется число равное произведению модулей этих векторов на  угла между ними угла между ними  Угол между двумя векторами   , имеющими общее начало, – это наименьший угол, на который нужно повернуть один из векторов вокруг точки приложения до положения, когда он станет сонаправленным с другим вектором , имеющими общее начало, – это наименьший угол, на который нужно повернуть один из векторов вокруг точки приложения до положения, когда он станет сонаправленным с другим вектором Физический смысл скалярного произведения- скалярное произведение двух векторов равно работе силы перемещения второго вектора вдоль первого Направляющие косинусы вектора пропорциональны его координатам 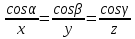 Угол между прямыми – следует из формулы нахождения угла между векторами  Угол между прямой и плоскостью (за угол между прямой и плоскостью будем брать угол между прямой и ее проекцией на заданную плоскость)   Векторным произведением двух векторов 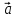  будем называть такой вектор будем называть такой вектор 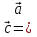  заданный в прямоугольной системе координат трехмерного пространства такой, что: заданный в прямоугольной системе координат трехмерного пространства такой, что:
Выражение векторного произведения через координаты  Смешанным произведением векторов 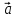  и и  называется число ( называется число (   , , ) равное скалярному произведению вектора ) равное скалярному произведению вектора  на векторное произведение векторов на векторное произведение векторов 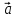  . . Площадь параллелепипеда 1/6(   , , ) )Если 3 вектора компланарны, то их смешанное произведение равно нулю, а параллелепипед, построенный на этих векторах - вырожденный Выражение смешанного произведения через координаты 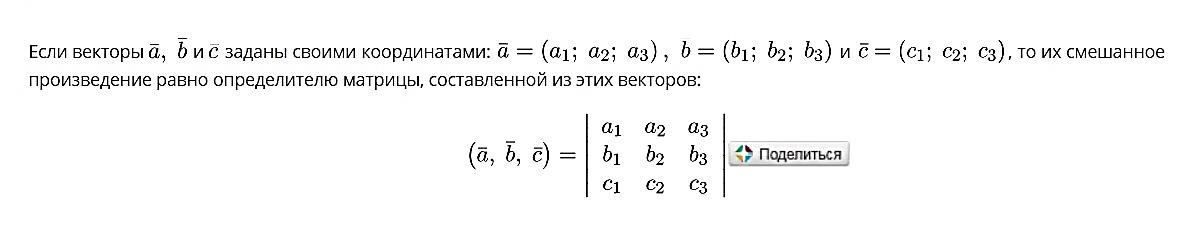 Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой. Уравнение прямой-прямая на плоскости задается уравнением ax + by + c = 0, где a, b, c - некоторые числа, причем a, b одновременно не равны нулю и составляют координаты вектора 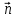 ,перпендикулярного этой прямой и называемого вектором нормали. ,перпендикулярного этой прямой и называемого вектором нормали.Уравнение прямой, выраженное через радиус-векторы  Параметрическое уравнение прямой на плоскости-  ,где ,где , т. , т.  , т.М(х,у) , т.М(х,у)Каноническое уравнение прямой на плоскости-  Уравнение прямой, проходящей через две точки-пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2, z 2 ), тогда уравнение прямой, проходящей через эти точки: Дробь  = k называется угловым коэффициентом прямой. = k называется угловым коэффициентом прямой.Уравнение прямой по точке и угловому коэффициенту- y=k*x+b .Угол между плоскостями – это угол между нормальными векторами этих плоскостей. Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость( d= 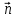 ={A;B:C} плоскости α, а число ={A;B:C} плоскости α, а число Нормальное уравнение прямой  Формула вычисления расстояния между двумя точками A(x1;y1) и B(x2;y2) на плоскости: 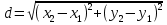 Формула вычисления расстояния между двумя точками A(x1; y1; z1) и B(x2; y2; z2) в пространстве: 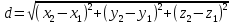 Взаимное расположение прямой и плоскости      Общее уравнение плоскости Ax+By+Cz+D=0 Векторное уравнение плоскости 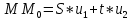 ,S,t ,S,t R R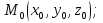   Параметрические уравнения плоскости 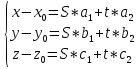  Уравнение плоскости в детерминантной форме 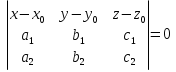 Уравнение плоскости, проходящие через три заданные точки 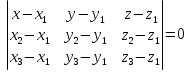 Уравнение плоыскости в отрезках 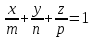 |




