|
|
Вычисление методом Монте-Карло. ВЫЧИСЛЕНИЕ МЕТОДОМ МОНТЕ-КАРЛО КОЛИЧЕСТВА ПЕРВИЧНЫХ ДЕФЕКТОВ В К. вычисление методом монтекарло количества первичных дефектов в кристаллическом кремнии, создаваемых протонами и нейтронами различных энергий
3. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ВЗАИМОДЕЙСТВИЯ НЕЙТРОНОВ И ПРОТОНОВ РАЗЛИЧНЫХ ЭНЕРГИЙ С КРЕМНИЕМ С ПОМОЩЬЮ GEANT4.
3.1. ФИЗИЧЕСКИЕ ПРОЦЕССЫ, ВКЛЮЧЕННЫЕ В GEANT4
В данной работе проводилось моделирование взаимодействия протонов и нейтронов с энергиями 1 МэВ, 14 МэВ, 63 МэВ. В этом энергетическом диапазоне учитывались следующие физические процессы:
compt – комптоновское рассеяние
conv – образование e+e- пар
eBrem – тормозное излучение
eIoni – ионизационные потери электронов
msc – многократное рассеяние
annihil – аннигиляция легких частиц
hIoni – ионизационные потери адронов
LElastic – упругое взаимодействие адронов
ProtonInelastic – неупругое ядерное взаимодействие протонов
NeutronInelastic – неупругое ядерное взаимодействие нейтронов
LCapture – захват нейтрона
Fission – распадный процесс, вызываемый нейтронами
К ядерным реакциям относятся ядерные взаимодействия упругого и неупругого типа, захват нейтрона, а так же распадный процесс, вызываемый нейтронами.
Данные о сечениях взаимодействия нейтронов в Geant4 содержатся в библиотеке G4NDL, которая позволяет моделировать прохождение нейтронов с энергиями от тепловых до 20 МэВ. В диапазоне энергий до 20 МэВ в Geant4 применяются экспериментальные данные из библиотеки G4NDL, а в диапазоне выше 20 МэВ применяется следующая экстраполяция:
=F(En)p12ln(N)[1+A1/3-p2(1-1/A1/3)] , (8)
где F – корректирующий коэффициент, N –количество нейтронов, En – энергия нейтронов в ГэВ, A – массовое число; p1 и p2 – параметры выбранной физической модели [4]. В данной работе использована модель промежуточного ядра, т.к. она наиболее точно описывает взаимодействие нейтронов с кремнием в используемом энергетическом диапазоне.
3.2. УСТАНОВКА И ЭКСПЛУАТАЦИЯ GEANT4
Подробная инструкция по установке Geant4 находится по адресу http://geant4.web.cern.ch/geant4/G4UsersDocuments/UsersGuides/InstallationGuide/html/index.html. Тем не менее, существует ряд нетривиальных особенностей, касающихся установки и настройки Geant4, на которые следует обратить внимание.
1. Существует два основных варианта установки Geant4: под Windows и под Linux (или любую другую Unix-подобную систему). Для установки Geant4 под Windows потребуется среда программирования Microsoft Visual C++ 6 с установленным Service Pack 5, а так же оболочка Cygwin, эмулирующая работу Unix-терминала в Windows. Cygwin можно скачать с сайтаhttp://www.cygwin.com. После установки Cygwin процедура установки Geant4 под Windows ничем не отличается от аналогичной процедуры под Linux за исключением настройки некоторых переменных окружения, описание которых содержится в инструкции по установке Geant4.
2. Для нормального функционирования Geant4 потребуется библиотека CLHEP(A Class Library for High Energy Physics), включающая описания генераторов случайных чисел, необходимых для работы Geant4. Найти её исходные модули и готовые для использования библиотеки можно по адресу http://cern.ch/clhep/.
3. Далее необходимо скачать и распаковать исходный код Geant4 и файлы физических данных для ядерных и электромагнитных взаимодействий (G4NDL, G4EMLOW, PhotonEvaporation,RadiativeDecay). Последние версии всегда можно найти по адресу http://cern.ch/geant4/.
4. После того, как все необходимые исходные коды скачаны и распакованы, можно приступать к установке Geant4 – т.е. к компиляции библиотек, входящих в состав исходного кодаGeant4. В комплекте с исходными кодами Geant4 поставляется утилита Configure, облегчающая установку Geant4. Для того чтобы начать установку, необходимо ввести команду
./Configure –install
после чего утилита конфигурации в интерактивном режиме начнет сбор сведений о конфигурации системы. После того, как процесс подготовки завершен, начинается компиляция библиотекGeant4, которая занимает достаточно продолжительный промежуток времени (1-5 часов в зависимости от быстродействия ЭВМ). В процессе компиляции на экране могут появляться различные предупреждения (warning), но как правило они не оказывают отрицательного влияния на ход установки. Если процесс компиляции успешно завершён, т.е. не возникло ошибок (error), то можно считать установку пакета Geant4 завершенной.
Порядок работы с Geant4 состоит в следующем: сначала составляется план эксперимента, изучаются основные свойства и характер взаимодействия экспериментальных частиц. Затем составляется программа на объектно-ориентированном языке C++, использующая библиотеки, входящие в состав Geant4. После этого исходные тексты программ компилируются, программа выполняется, и происходит анализ полученных результатов. По мере анализа полученных данных в программу вносятся изменения, затем процесс повторяется до тех пор, пока не будут получены удовлетворительные результаты.
Моделирование физического эксперимента с помощью Geant4 основано на методе Монте-Карло. Это предполагает ход физических процессов в эксперименте с наперед заданными вероятностями, чтобы обеспечить максимальную реалистичность эксперимента.
Моделирование прохождения нейтронов в веществе включает в себя: описание геометрии детектора, описание химического состава входящих в эксперимент материалов, описание типов частиц, участвующих в эксперименте, описание физических процессов и первичного события (вылет первичной частицы из источника).
● Описание химического состава материалов, входящих в эксперимент:
В качестве материала для детектора был использован природный кремний с плотностью 2,33 г/см3 и молярной массой 28,09 г/моль. Состав природного кремния: Si28 – 92,23%, Si29 – 4,68%, Si30 – 3,09%.
● Описание геометрии детектора:
В качестве экспериментального объема используем параллелепипед из кремния и разместим его в начале координат, т.е. центр параллелепипеда находится в точке (0, 0, 0). В случае толстой мишени толщина параллелепипеда 50 см, в случае тонкой мишени 1мм.
● Описание типов частиц, участвующих в эксперименте:
Для того, чтобы в эксперименте участвовали какие-либо частицы, их необходимо вначале описать. В нашем эксперименте будем рассматривать протоны, нейтроны, гамма-кванты, электроны, позитроны, μ+, μ-, 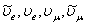 , а также альфа-частицы, дейтроны и другие частицы. , а также альфа-частицы, дейтроны и другие частицы.
Рассмотрим пример выходных данных эксперимента прохождения нейтрона с энергией 15 МэВ в кремниевом кубике 20х20х20 см3. Данные представлены в текстовом виде. Каждая частица имеет свой номер трека (Track ID) и номер родительской частицы (Parent ID). На каждом шаге (Step) указываются координаты частицы (X, Y, Z), её энергия (KinE), энергетические потери (dEStep), длина пробега на текущем шаге (StepLeng), полная длина пробега (TrackLeng), место нахождения (Volume) и тип взаимодействия (Process).
*********************************************************************************** G4Track Information: Particle = neutron, Track ID = 1, Parent ID = 0
**********************************************************************************
Step# X Y Z KineE dEStep StepLeng TrakLeng Volume Process
0 -10 cm 0 fm 0 fm 15 MeV 0 eV 0 fm 0 fm World initStep
1 -2.49 cm 0 fm 0 fm 15 MeV 0 eV 7.51 cm 7.51 cm World NeutronInelastic
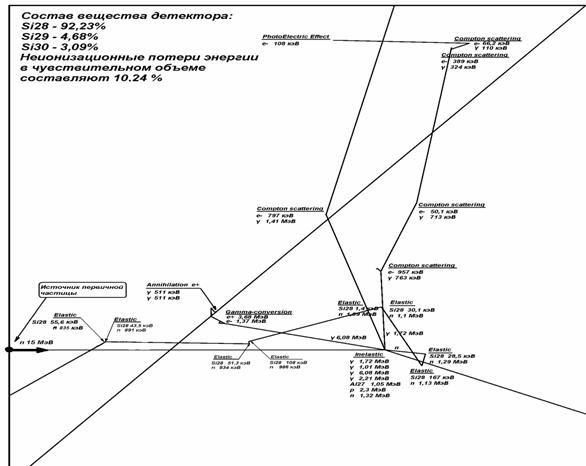
Визуализация осуществлялась с помощью программного средства FukuiRenderer DAWN, позволяющего отображать траектории частиц и составляющие части детектора в виде трехмерного изображения. Трехмерное изображение представлено в виде проекции на плоскость (Рис. 4) с нанесенными на неё траекториями и энергиями частиц, участвующих во взаимодействиях, произведенных первичной частицей.
|
Рис. 4
|
Примечание: полная история движения и взаимодействий вторичных частиц, соответствующая этому рисунку, представлена в приложении 1.
3.3. ОПИСАНИЕ ОСНОВНЫХ ПАРАМЕТРОВ ЗАДАЧИ
Численное моделирование проводится методом Монте-Карло с помощью пакета Geant4. Процедура моделирование прохождения нейтронов и протонов в кремнии представляет повторяющийся процесс запуска начальной частицы (протона или нейтрона) с заданной энергией. После того, как частица вылетела из своего начального положения (источника первичных частиц) и провзаимодействовала в объеме детектора, регистрируются координаты и энергии вторичных частиц, заполняются угловые и энергетические спектры. Затем процесс продолжается до тех пор, пока не будет накоплено нужное количество ядер отдачи.
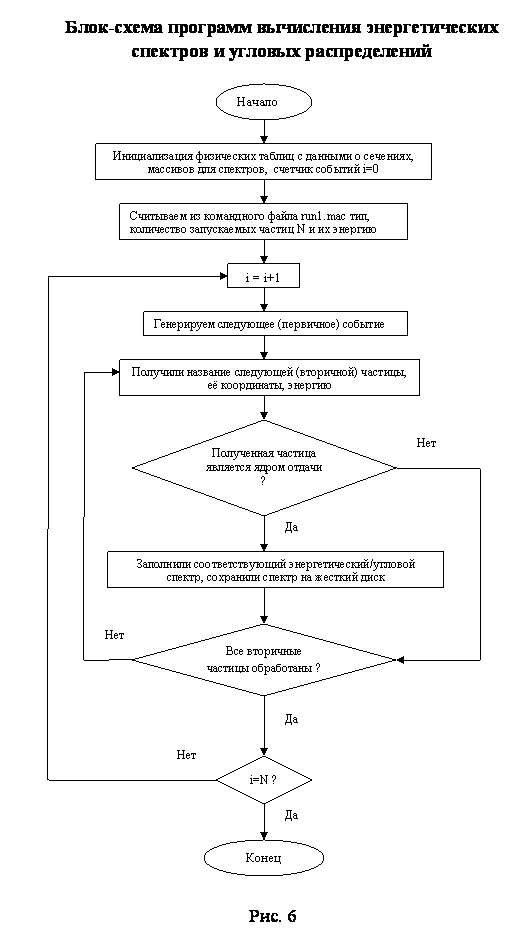
Блок схема для программы моделирования и общая картина эксперимента представлены ниже.

3.4. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ
Моделирование проводилось на операционной системе Linux Mandrake 9.0. Для вычислений использовалась ЭВМ с процессором 1,3 МГц, оперативной памятью 256 Мб. Версия пакетаGeant4 4.4.1 с патчем N1. Последнюю версию Geant4 можно скачать с сайта http://cern.ch/geant4/.
Энергетические спектры.
В результате моделирования прохождения протонов и нейтронов в природном кремнии были получены энергетические спектры ядер отдачи и угловые распределения. В таблице 1 представлены условия и результаты моделирования.
Таблица 1.
|
Толстая пластина, 50 см
|
Тонкая пластина, 1мм
|
Час-тица
|
n
|
p
|
n
|
p
|
E
|
1 МэВ
|
14 МэВ
|
63 МэВ
|
14 МэВ
|
63 МэВ
|
1 МэВ
|
14 МэВ
|
63 МэВ
|
14 МэВ
|
63 МэВ
|
n
|
3,5•104
|
1,3•105
|
105
|
3•108
|
1,1•106
|
1,7•106
|
106
|
3•105
|
106
|
1,5•105
|
N
|
106
|
106
|
106
|
4•104
|
2•105
|
104
|
104
|
104
|
104
|
104
|
t
|
4
|
10
|
25
|
10
|
18
|
5
|
3
|
5
|
3
|
9
|
ΔE
|
32029
|
131117
|
283965
|
6075
|
103456
|
388
|
4271
|
9212
|
1684
|
9224
|
ζ
|
91,5
|
7,2
|
4,5
|
0,0001
|
0,15
|
0,023
|
0,03
|
0,05
|
0,01
|
0,1
|
D
|
3660
|
4034
|
11358
|
0,08
|
376
|
0,9
|
17,1
|
123
|
7
|
246
|
E – энергия налетающих частиц, n – количество налетевших частиц,
N-количество образованных ядер отдачи, t-время моделирования
(минуты), ΔE-полная энергия образованных ядер отдачи (МэВ),
ζ – доля неионизационных потерь энергии по отношению к полным потерям энергии (%),
D – количество дефектов от одной налетающей частицы.
Доля неионизационных потерь энергии вычислялась по формуле:
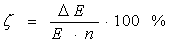 . (9) . (9)
Количество дефектов от одной налетающей частицы определяется выражением:
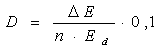 . (10) . (10)
-
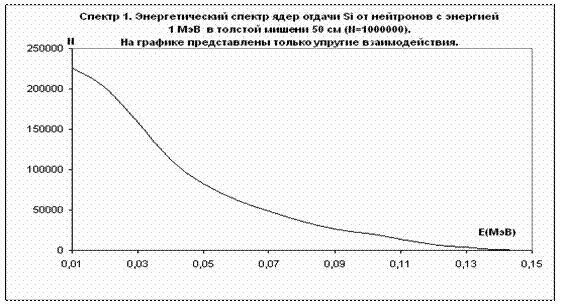
|
Рис.7
|
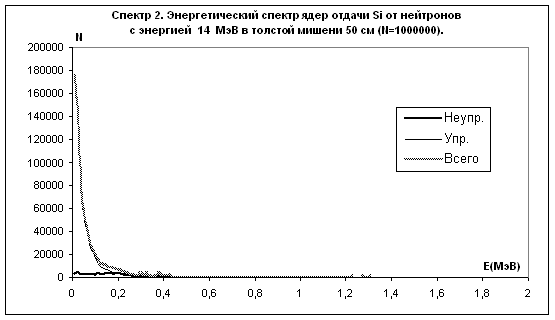
|
Рис.8
|
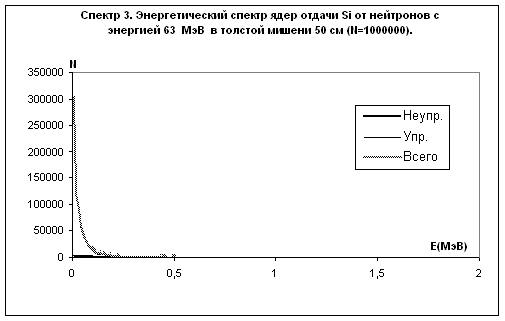
|
Рис.9
|
|
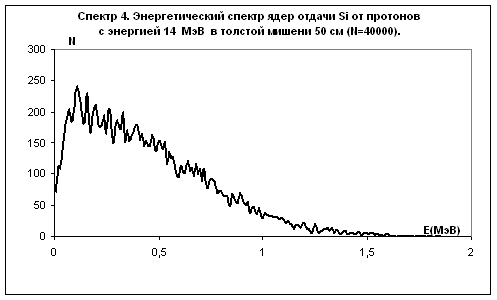
Рис.10
|
|
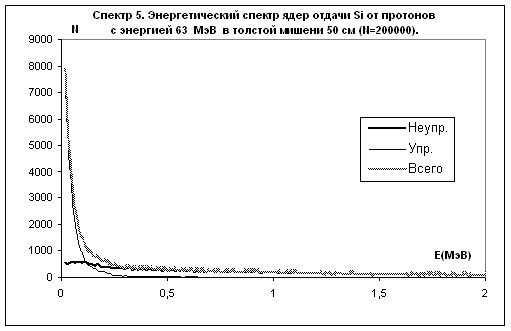
Рис.11
|
|
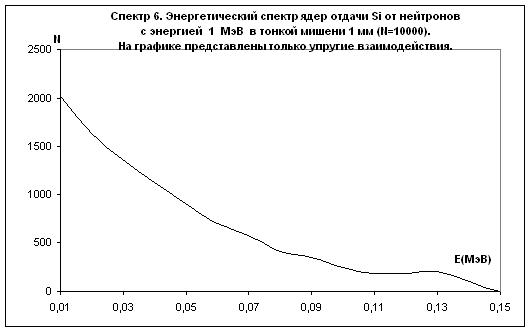
Рис.12
|
|
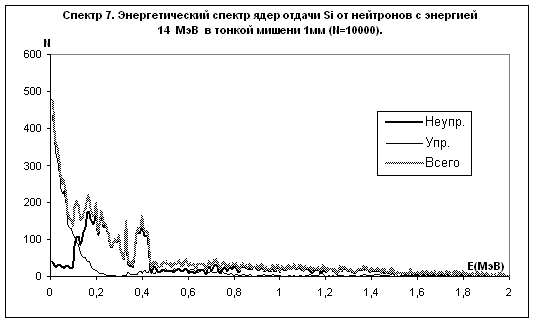
Рис.13
|
|
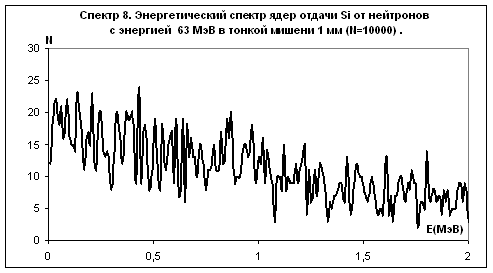
Рис.14
|
|
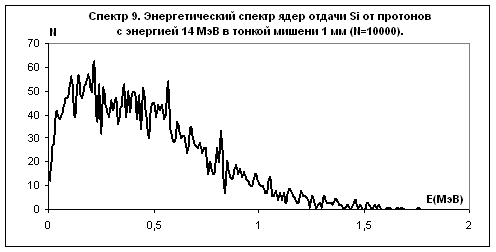
Рис.15
|
|
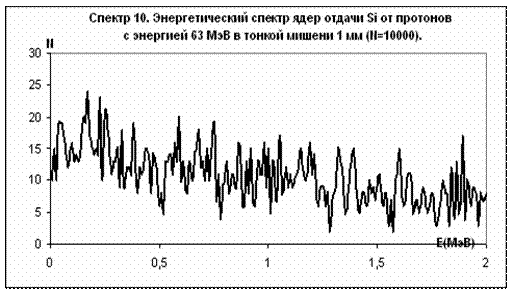
Рис.16
|
Примечание: на рис. 10 приведены только неупругие взаимодействия. Количество упругих взаимодействий равно 26272. Все упругие взаимодействия образуют ядра отдачи c энергией до 10 кэВ. На рис. 11 не показаны ядра отдачи с энергией меньше 10 кэВ. В первый бин спектра входят 100258 ядер от упругих взаимодействий. На рис. 14, рис. 15, рис. 16 приведены результаты только неупругих взаимодействий. Упругие взаимодействия составляют 60% от общего числа взаимодействий и входят в первый бин спектра.
|
|
|
 Скачать 0.62 Mb.
Скачать 0.62 Mb.












