ЭВМ и ПУ. Вычислительные машины, системы и сети - курс лекций. Вычислительные машины, системы и сети. Курс лекций

• Название: Вычислительные машины, системы и сети. Курс лекций
• Анкор: ЭВМ и ПУ
• Дата: 04.03.2021
• Размер: 1.45 Mb.
• Имя файла: Вычислительные машины, системы и сети - курс лекций.doc
• Тип: Курс лекций; #181794
• страница: 9 из 23

14. Сумматор

Операционный узел состоит из устройств, в которых обрабатывается и хранится информация, а именно: счетчиков, регистров, шифраторов, дешифраторов, сумматоров, схем сравнения, блоков памяти и т. п. Используя набор этих устройств, можно производить обработку поступающей информации. Результатом ее обработки является выходная информация.

Сумматор - логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие дополнительные операции: учет знаков чисел, выравнивание порядков слагаемых и тому подобное.
Сумматоры классифицируются по разным признакам:

1. В зависимости от системы исчисления:

• 
  Двоичные
  
• 
  Двоично-десятичные (двоично кодированые)
  
• 
  Десятичные
  
• 
  Прочие (пример: амплитудные)
  

2. По количеству одновременно обрабатываемых разрядов складываемых чисел:

• 
  Одноразрядные
  
• 
  Многоразрядные
  

3. По числу входов и выходов одноразрядных двоичных сумматоров:

• 
  Четвертьсумматоры, характеризующиеся наличием двух входов, на которые подаются два одноразрядных числа, и одним выходом, на котором реализуется их арифметическая сумма;
  
• 
  Полусумматоры, характеризующиеся наличием двух входов, на которые подаются одноимённые разряды двух чисел, и двух выходов: на одном реализуется арифметическая сумма в данном разряде, а на другом ≈ перенос в следующий (более старший разряд);
  
• 
  Полные одноразрядные двоичные сумматоры, характеризующиеся наличием трех входов, на которые подаются одноименные разряды двух складываемых чисел и перенос из предыдущего (более младшего) разряда, и двумя выходами: на одном реализуется арифметическая сумма в данном разряде, а на другом ≈ перенос в следующий (более старший разряд).
  

4. По способу представления и обработки складываемых чисел многоразрядные сумматоры подразделяются на:

• 
  Последовательные, в которых обработка чисел ведется поочередно, разряд за разрядом, на одном и том же оборудовании;
  
• 
  Параллельные, в которых слагаемые складываются одновременно по всем разрядам, и для каждого разряда имеется свое оборудование.
  

Построение двоичных сумматоров обычно начинается с сумматора по модулю 2. На рисунке 14.1 приведена таблица истинности этого сумматора. Ее можно получить исходя из правил суммирования в двоичной арифметике.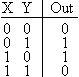


Рисунок 14.1 – Таблица истинности сумматора по модулю 2.
Схема сумматора по модулю 2 приведена на рисунке 14.2.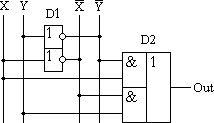


Рисунок 14.2 - Принципиальная схема, реализующая таблицу истинности сумматора по модулю 2.
Сумматор по модулю 2 (для двоичной арифметики его схема совпадает со схемой исключающего "ИЛИ") изображается на схемах как показано на рисунке 14.3.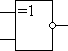


Рисунок 14.3. Изображение схемы, выполняющей логическую функцию исключающего "ИЛИ".
Сумматор по модулю 2 выполняет суммирование без учета переноса. В полном двоичном сумматоре требуется учитывать перенос, поэтому требуются схемы, позволяющие формировать перенос в следующий двоичный разряд. Таблица истинности такой схемы, называемой полусумматором, приведена на рисунке 14.4.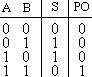


Рисунок 14.4 - Таблица истинности полусумматора.
Принципиальная схема, реализующая таблицу истинности полусумматора представлена на рисунке 14.5. Полусумматор изображается на схемах как показано на рисунке 14.6.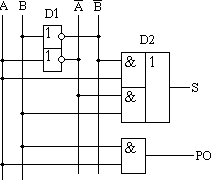


Рисунок 14.5 - Принципиальная схема, реализующая таблицу истинности полусумматора.

Рисунок 14.6 - Изображение полусумматора на схемах.
Схема полусумматора формирует перенос в следующий разряд, но не может учитывать перенос из предыдущего разряда, поэтому она и называется полусумматором. Таблицу истинности полного двоичного одноразрядного сумматора можно получить из правил суммирования двоичных чисел. Она приведена на рисунке 14.7. В обозначении входов использовано следующее правило: в качестве входов использованы одноразрядные числа A и B; перенос обозначен буквой P; для обозначения входа переноса используется буква I (сокращение от английского слова input – вход); для обозначения выхода переноса используется буква O (сокращение от английского слова output – выход).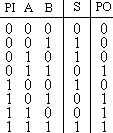


Рисунок 14.7 - Таблица истинности полного двоичного одноразрядного сумматора.
По таблице 14.7 составим схему полного двоичного одноразрядного сумматора. Эта схема приведена на рисунке 14.8. Ее можно минимизировать, но это несколько усложняет принципы построения сумматоров, поэтому вопросы минимизации рассматриваться не будут.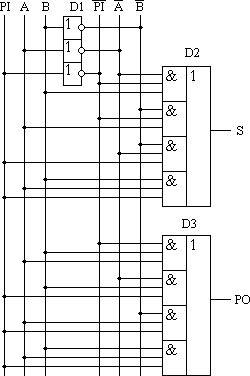


Рисунок 14.8. Принципиальная схема, реализующая таблицу истинности полного двоичного одноразрядного сумматора.
Полный двоичный одноразрядный сумматор изображается на схемах как показано на рисунке 14.9.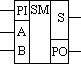


Рисунок 14.9 Изображение полного двоичного одноразрядного сумматора на схемах.
Для того чтобы получить многоразрядный сумматор, достаточно соединить входы и выходы переносов соответствующих двоичных разрядов.