СТАТИСТИКА_ответы к экзамену. Вопрос 1 Предмет и методы статистики. Задачи статистики в государственном и муниципальном управлении. Статистика
 Скачать 1.84 Mb. Скачать 1.84 Mb.
|
|
Вопрос №7 Мода и медиана, значение и методы расчета. Мода — это наиболее часто встречающееся значение признака в совокупности. В интервальных вариационных рядах сначала находят модальный интервал. В найденном модальном интервале конкретное значение моды определяют по формуле: 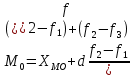 Где 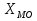 - нижняя граница модального интервала; d— величина интервала; - нижняя граница модального интервала; d— величина интервала; 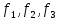 - частоты предмодального, модального и посмодального интервалов. - частоты предмодального, модального и посмодального интервалов.Мода широко применяется в коммерческой деятельности. Медиана — значение признака, находящееся посредине рассматри ваемого ряда. Она указывает центр распределения единиц совокупно сти и делит ее на две равные части. При отыскании медианы сначала определяется ее порядковый номер в ряду распределения. При нечетном числе единиц в ряду: 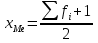 При четном числе единиц в ряду: 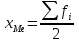 Т.е. полусумма из двух соседних центральных значений. В интервальном ранжированном ряду, зная порядковый номер медианы, по накопленным частотам отыскивается медианный интервал, в котором определяется конкретное значение медианы по формуле: 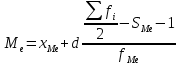 Где 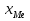 - нижняя граница медианного интервала; - нижняя граница медианного интервала; 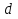 - величина интервала; - величина интервала; 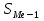 - частота, накопленная да медианного интервала; - частота, накопленная да медианного интервала; 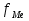 - частота медианного интервала. - частота медианного интервала.Медиана используется при контроле качества продукции и технологического процесса на промышленных предприятиях, при изучении распределения домохозяйств по величине дохода и т. д. |Н Мода и медиана имеют преимущества перед средними арифметическими для ряда распределения с открытыми интервалами. Вопрос № 8. Показатели вариации и их значение, методика их расчета. Вариация наблюдается и в пределах однородной совокупности или однородной группы. Изучение вариации предполагает использование следующих приемов: построение вариационного ряда (ряда распределения), его графическое изображение и исчисление основных характеристик распределения. Вариационные ряды бывают дискретные и интервальные. Для анализа вариационных рядов используются:
Для оценки вариации признака используют следующие показатели. Размах вариации: 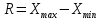 Где 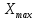 и и 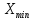 - максимальное и минимальное значение признака. - максимальное и минимальное значение признака.Однако этот показатель далеко не совершенен, так как в его построении участвуют лишь крайние значения признака, которые могут быть случайными. Среднее линейное отклонение: 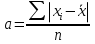 - простое, для несгруппированных данных; - простое, для несгруппированных данных;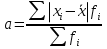 – взвешенное, для сгруппированных данных. – взвешенное, для сгруппированных данных.Среднее квадратическое отклонение: 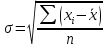 – простое; – простое;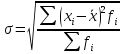 – взвешенное. – взвешенное.Среднее квадартическое отклонение является наиболее распространенным показателем вариации. Установлено, что в симметричных или умеренно асимметричных распределениях соотношения между ними можно записать: 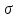 =1,25а. =1,25а.Среднее квадратическое отклонение минимально при вычислении его средней арифметической величины; это же относится и к дисперсии, которая представляет собой квадрат среднего квадратического отклонения. Дисперсия: 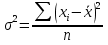 - широко применяется в дисперсионном анализе. - широко применяется в дисперсионном анализе.Коэффициент осцилляции: 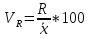 Относительное отклонение: 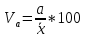 Коэффициент вариации: 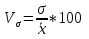 Наиболее объективным показателем является коэффициент вариации который, применяют не только для сравнения вариации, но и для характеристики однородности совокупности. Распределение считается близким к нормальному, а совокупность однородна, если коэффициент вариации не превышает 33%. Вопрос №9. Роль и значение графического метода. В результате сводки и дальнейшей обработки, данных отчетности, различного рода обследований, переписей, наблюдений и т.п. экономист получает большое количество различных статистических показателей, которые он располагает в виде таблиц. Применение табличного метода значительно облегчает ориентацию в материале. Однако из этого не следует, что можно ограничиться одними таблицами. Для того, чтобы сделать дальнейший шаг в понимании материала, надо от табличного метода перейти к графическому. Графиком в статистике называется условные изображения статистических данных в виде различных геометрических образов: точек, линий, фигур и т.п. Главное достоинство графиков - наглядность. В статистике графики используются, во-первых, в целях широкой популяризации IX и для облегчения их восприятия неспециалистами. Поэтому в различного рода докладах, речах и сообщениях представление статистических данных часто осуществляется при помощи графиков. Графики облегчают ознакомление масс со статистическими данными, оживляют таблицу, делают ее более доступной. Во-вторых, графики широко используются для обобщения и анализа статистических данных. Они находят большое применив в исследовательской работе. Именно при помощи графиков легче уяснить закономерности развития, распределения и размещения явлений. При помощи графиков в ряде случаев можно сделать выводы, которые на базе табличного метода были бы затрудни-1ьными, В-третьих, надо еще указать и на контрольное значение графиков. Под этим следует понимать тот факт, что во многих случаях различного рода ошибки и неточности выявляются при применении графиков, т.е. они иногда являются контролером точности счётов и вычислений. В настоящее время графики прочно вошли в практику экономического анализа в с внедрением в статистическую работу новых математических методов и современной вычислительной техники на базе ПЭВМ, с использованием пакетов прикладных программ компьютерной графики. Наиболее распространёнными пакетами прикладных проявляются: «Ехсе1», «Stat Graff», «Super са11», «Hazard graphics» и др. Эти программы облегчают задачу исследователя в практическом применении графиков, так как с помощью дисплеев можно демонстрировать графики на световом экране, при необходимости оперативно изменяя в них одни данные, вводя другие и т. д. Такого рода графики в приняв могут заменить громоздкие таблицы компактными изображениями. Графики различаются по своему виду, и задача состоит в том, чтобы найти наиболее подходящий график. Нужно научиться правильно пользоваться орудием графического метода при изображении статистических данных. Кроме этого, график надо уметь строить, понимать принцип его построения. В противном случае можно выбрать правильный график, но сделать его таким, что он исказит действительную картину. Вопрос №10. Понятие и виды динамических рядов, основные показатели анализа рядов динамики и порядок их расчета. Ряд в статистике — это цифровые данные, показывающие, изменение явления во времени или в пространстве и дающие возможность производить статистическое сравнение явлений как в процессе их развития во времени, так и по различным формам и видам процессов. Благодаря этому можно обнаружить взаимную зависимость явлений. Процесс развития движения социальных явлений во времени в статистике принято называть динамикой. Для отображения динамики строят ряды динамики (хронологические, временные), которые представляют собой ряды изменяющихся во времени значений статистического показателя (например, число осуждённых за 10 лет), расположенных в хронологическом порядке. Их составными элементами являются цифровые значения данного показателя и периоды или моменты времени, к которым они относятся. Важнейшая характеристика рядов динамики — их размер (объём, величина) того или иного явления, достигнутых в определённых период или к определённому моменту. Соответственно, величина членов ряда динамики — его уровень. Различают начальный, средний и конечный уровни динамического ряда. Начальный уровень показывает величину первого, конечный — величину последнего члена ряда. Средний уровень представляет собой среднюю хронологическую вариационного рада и исчисляется в зависимости от того, является ли динамический ряд интервальным или моментным. Ещё одна важная характеристика динамического ряда — время, прошедшее от начального до конечного наблюдения, или число таких наблюдений. Существуют различные виды рядов динамики, их можно классифицировать по следующим признакам. 1) В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных и производных показателей (относительных и средних величин). 2) В зависимости от того, как выражают уровни ряда состояние явления на определённые моменты времени (на начало месяца, квартала, года и т.п.) или его величину за определённые интервалы времени (например, за сутки, месяц, год и т.п.), различают соответственно моментные и интервальные ряды динамики. Моментные ряды в аналитической работе правоохранительных органов используются сравнительно редко. В теории статистики выделяют рады динамики и по ряду других классификационных признаков: в зависимости от расстояния между уровнями — с равностоящими уровнями и неравностоящими уровнями во времени; в зависимости от наличия основной тенденции изучаемого процесса — стационарные и не стационарные. 11.Методы выявления основной тенденции динамических рядов. ДАВЫДОВА Д. 12.Прогнозирование на основе экстраполяции тренда. ДАВЫДОВА Д. Вопрос № 13. Показатель сезонных колебаний На специфику изменения уровней рядов внутригодовой динамики могут оказывать влияние как факторы, образующие их составные компоненты (тренд, периодические колебания,случайные отклонения), так и внешние причины, обусловленные характером сбора и обработки исходной информации. В статистике существует ряд методов изучения и измерения сезонных колебаний. Самый простой заключается в построении специальных показателей, которые называются индексами сезонности iS. Совокупность этих показателей отражает сезонную волну. В общем виде они определяются отношением исходных (эмпирических) уровней ряда динамики (уi) к теоретическим (расчетным) уровням (уt) , выступающим в качестве базы сравнения: 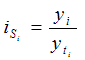 Поскольку на сезонные колебания могут накладываться случайные отклонения, для их устранения производится усреднение индивидуальных индексов одноименных внутригодовых периодов анализируемого ряда динамики. Поэтому для каждого периода годового цикла определяются обобщенные показатели в виде средних индексов сезонности: 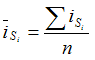 В зависимости от характера тренда, формула принимает следующие формы: 1) Для рядов внутригодовой динамики с ярко выраженной основной тенденцией развития(т.н.нестационарные ряды динамики). Выступающие при этом, в качестве переменной базы сравнения, теоретические уровни (уt) представляют, своего рода, "среднюю ось кривой", так как их расчет основан на положениях метода наименьших квадратов. Поэтому измерение сезонных колебаний на базе переменных уровней тренда называется способом переменной средней. 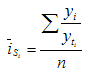 2) Для рядов внутригодовой динамики, в которых повышающийся (снижающийся) тренд отсутствует или он незначителен (т. н. стационарные ряды динамики). В данной формуле базой сравнения является общий для анализируемого ряда динамики средний уровень. Поскольку для всех эмпирических уровней анализируемого ряда динамики этот общий средний уровень является постоянной величиной, то применение формулы называется способом постоянной средней. Коэффициент сезонности или индекс сезонности, в данном случае представляет собой отношение средней из фактических уровней одноименных месяцев к средней из выровненных (теоретических, расчетных) данных по тем же месяцам, выступающим в качестве базы сравнения: 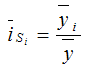 Вопрос № 14. Экономическое значение индексов, особенности их расчета Индекс – это специфический, статистический метод исследования. Индекс (в пер. с лат.) – показатель, указатель. В теории индексов тот показатель, изменение которого характеризует индекс, называется индексируемой величиной. Показатель, который вводится в индекс с целью преодоления несуммарности элементов изучаемого явления, называется весом индекса. Индексы используются:1) для характеристики общего изменения всех элементов сложного явления во времени, в пространстве и по сравнению с планом (нормой); 2) для оценки роли факторов в изменении сложных явлений; 3) для анализа влияния структурных сдвигов в экономике. Существует два способа расчета индексов цен: индексы цен Пааше и Лайспейреса. Данный способ предлагает использование весов базисного периода . Впервые был введен в 1864 году экономистом Э.Ласпейресом. Индекс цен Ласпейреса показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но на товары реализованные в базисном периоде. Индекс цен Пааше — это агрегатный индекс цен с весами (количество реализованного товара) в отчетном периоде. Идеальный индекс цен Фишера Представляет собой среднюю геометрическую из произведений двух 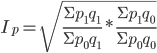 агрегатных индексов цен Ласпейреса и Пааше.Идеальность заключается в том, что индекс является обратимым во времени, то есть при перестановке базисного и отчетного периодов получается обратный индекс (величина обратная величине первоначального индекса). агрегатных индексов цен Ласпейреса и Пааше.Идеальность заключается в том, что индекс является обратимым во времени, то есть при перестановке базисного и отчетного периодов получается обратный индекс (величина обратная величине первоначального индекса).Вопрос № 15. Индексный анализ объемных показателей Для получения общего итога и построения агрегатного индекса несоизмеримого объемного показателя нужно предварительно соизмерить отдельные значения этого показателя. Исходя из экономической сущности явления, нужно найти общую меру и использовать ее в качестве коэффициента соизмерения. Такой общей мерой для объемных показателей являются связанные с ними качественные показатели. Так, объемы различных видов продукции могут быть соизмерены с помощью цены (р), себестоимости (z) и трудоемкости (t) этих продуктов. Умножая индексируемый объемный показатель на тот или иной качественный показатель, не только обеспечивается возможность суммирования, но одновременно учитывается также роль каждого элемента, например продукта, в реальном экономическом процессе, т. е. его статистический вес в этом процессе. Чтобы индекс отражал только изменение индексируемого объемного показателя, веса в его числителе и знаменателе фиксируются на уровне одного и того же периода. В практике экономической работы в индексах динамики объемных показателей веса обычно фиксируются на уровне базисного периода (см. формулу). Это обеспечивает возможность построения систем взаимосвязанных индексов. Для индивидуальных объемных показателей (объем реализации, объем производительности продукции, посевная площадь) веса выбираются на уровне базисного периода. Например: 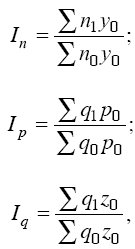 где In– сводный индекс урожайности; I – сводный индекс стоимости товарооборота; Iq – сводный индекс себестоимости. Вопрос № 16. |
