СТАТИСТИКА_ответы к экзамену. Вопрос 1 Предмет и методы статистики. Задачи статистики в государственном и муниципальном управлении. Статистика
 Скачать 1.84 Mb.
|
|
Индексный анализ средних показателей Преобразование агрегатного индекса в средний из индивидуальных (групповых) индексов производится следующим образом: либо в числителе, либо в знаменателе агрегатного индекса индексируемый показатель заменяется его выражением через соответствующий индивидуальный индекс. Если такую замену сделать в числителе, то агрегатный индекс будет преобразован в средний арифметический, если же в знаменателе – то в средний гармонический из индивидуальных индексов. Например, известен индивидуальный индекс физического объема iq = q1/q0 и стоимость продукции каждого вида в базисном периоде (q0p0). Исходной базой построения среднего из индивидуальных индексов служит сводный индекс физического объема: 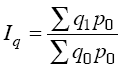 Из имеющихся данных непосредственно суммированием можно получить только знаменатель формулы. Числитель же может быть получен перемножением стоимости отдельного вида продукции базисного периода на индивидуальный индекс: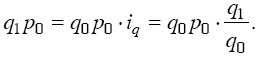 Тогда формула сводного индекса примет вид: 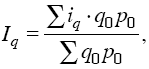 Допустим, что в наличии имеется информация о динамике объема выпуска каждого вида продукции (q) и стоимости каждого вида продукции в отчетном периоде (p1q1). Для определения общего изменения выпуска продукции предприятия в этом случае удобно воспользоваться формулой Пааше: 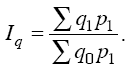 Числитель формулы можно получить суммированием величин q1P1, а знаменатель – делением фактической стоимости каждого вида продукции на соответствующий индивидуальный индекс физического объема продукции, т. е. делением: p1q1/iq, тогда: Применение той или иной формулы индекса физического объема (агрегатного, среднего арифметического и среднего гармонического) зависит от имеющейся в распоряжении информации.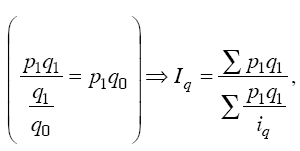 Вопрос №17. Методы изучения связей между экономическими явлениями. Какие экономические задачи решаются с помощью корреляционного метода? Метод сравнения параллельных рядов - самый простой метод анализа экономических явлений. Сначала показатели факторного признака I ранжируются (в восходящем или нисходящем порядке в зависимости от исследуемого явления или процесса), затем добавляются показатели результативного признака. Путем сравнения расположенных та ким образом значений признака выявляется существование связей и их направление. Метод аналитических группировок считается одним из основных методов изучения связей между экономическими явлениями. Процесс установления связей начинается с группировки единиц совокупности по факторному признаку. Затем приступают к вычислению синтети ческих показателей (относительных и средних величин) для резуль тативного признака по группам, на которые была разбита совокуп ность. Существенность связи между признаками доказывается на основе применения дисперсионного метода. На основе дисперсионного анализа производятся:
В основе применения дисперсионного анализа лежит закон разло жения дисперсий (вариаций) признака на составляющие. Метод корреляционно-регрессионный используется для исследования интенсивности и формы причинных влияний. Суть корреляционно-регрессионного анализа заключается в следующем.
Для сравнения роли различных факторов в формировании ре зультата, определяются коэффициенты эластичности: 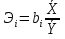 где bi - коэффициенты регрессии при соответствующем факторе. Коэффициент эластичности показывает, на сколько процентов в среднем изменяется результат с изменением фактора1% Вопрос 18. Построение корреляционно-регрессионной модели и её интерпретация. Для исследования интенсивности, вида и формы причинных влияний широко применяется корреляционный и регрессионный анализ. Понятия «корреляции» и «регрессии» непосредственно связаны между собой. Однако в корреляционном анализе оценивается сила (теснота) связи между явлениями, в регрессионном исследуется ее форма. Следовательно, суть корреляционно-регрессионного анализа заключается в следующем: 1) Сначала устанавливаются результативный признак (y) и факторные (x). Если изучается влияние одного фактора на результат, это называют парной корреляцией, а влияние нескольких факторов на результат - множественной корреляцией. По направлению связи могут быть прямые (положительные) и обратные (отрицательные). 2) Затем осуществляется проверка информации на однородность и нормальность распределения. Однородность совокупности проверяется коэффициентом вариации по факторным признакам, который не должен превышать 33%. 3) Установление наличия и направления корреляционной зависимости между результативным (Y)и факторным признаками на основе аналитической группировки. Все единицы совокупности разбиваются на группы по факторному признаку, и в каждой группе рассчитывается средняя величина результативного признака. Данные этой группировки можно изобразить графически построить линию регрессии, т. е. вид которой позволяет судить не только о наличии связи, но и дает представление о форме корреляционной связи (прямолинейная или криволинейная). 4) Определение степени тесноты связи и оценка ее существенности. Теснота парной корреляции измеряется коэффициентом корреляции (r) - при линейной связи и корреляционным отношением (n) - при линейной и криволинейной зависимости. Коэффициент корреляции может принимать значение в пределах от -1 до +1. Знак коэффициента корреляции характеризует направление связи. Знак «+» - связь прямая, знак «-» - обратная. Абсолютная величина показывает силу связи: чем ближе к 1, тем сильнее связь. 5) Определить тип уравнения регрессии можно, исследуя зависимость графически на основе группировки. Так, если результативный и факторный признаки возрастают примерно одинаково, то это свидетельствует о том, что связь между ними линейная; если же один признак увеличивается, а другой неравномерно уменьшается - связь гиперболическая. Если с увеличением значений фактора результативный признак сначала растет, а потом снижается, то связь параболическая. 6) Построение корреляционно-регрессионной модели. Изучение множественной корреляции следует начинать с анализа матрицы парных коэффициентов корреляции, которая позволяет произвести отбор коллинеарных факторов, т. е. факторов, у которых связь с результатом слабее, чем между собой. Целесообразно оставить тот фактор, у которого связь с результатом выше, чем с соответствующим фактором. 7) Экономическая интерпретация корреляционно-регрессионной модели. Коэффициенты регрессии (b), которые показывают, что на эту величину в среднем изменится результат при изменении соответствующего фактора на единицу своего измерения при условии постоянства других факторов, включенных в модель. Параметр (а), как правило, экономического смысла не несет, а является началом отсчета. 8) Для измерения тесноты связи между изменениями величины результата и изменениями значений факторов определяется совокупный (множественный) коэффициент корреляции 9) Для сравнения роли различных факторов в формировании результата, определяются коэффициенты эластичности. Коэффициент эластичности показывает, на сколько процентов в среднем изменяется результат с изменением фактора на 1%. Вопрос №19 Определение коэффициентов корреляции по знакам отклонений от средних (коэффициент Фехнера) и ранговый коэффициент корреляции (коэффициент Спирмена). Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. На практике для определения тесноты связи используется коэффициент Фехнера: 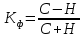 , где С – число совпадений знаков индивидуальных значений от средней величины по фактору и результату (например, «+» и «+»; «минус» и «минус»); Н – число несовпадений знаков отклонений индивидуальных значений от средней величины по фактору и результату (например, «+» и «минус»; «минус» и «+»).Коэффициент Фехнера целесообразно использовать для установления факта наличия связи при небольшом объеме исходной информации. 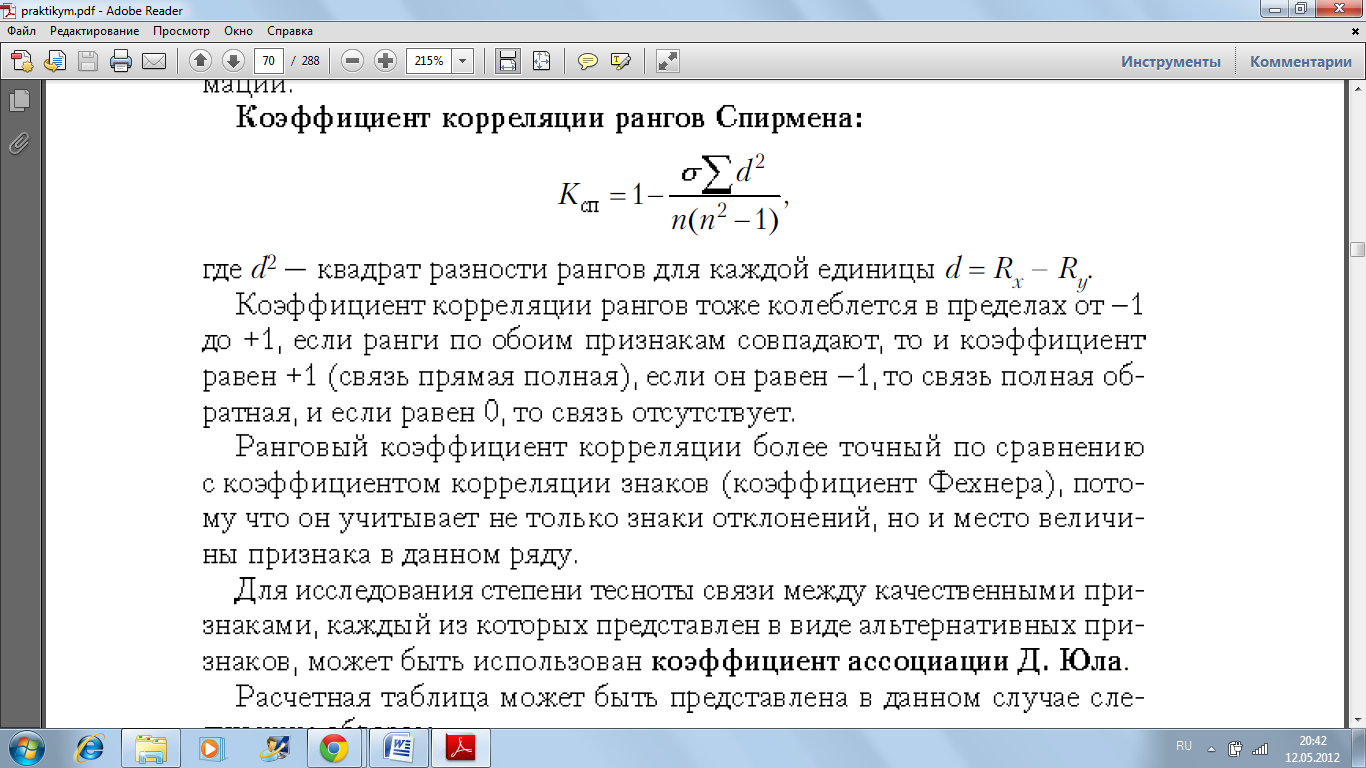 Вопрос № 20. Применение корреляционно-регрессивной модели для прогнозирования и планирования. Корреляционные модели нашли применение во внутризаводском планировании на предприятиях. Одним из элементов оперативного планирования производства являются календарно-плановые нормативы. Однако корреляционные модели нашли применение не только в планировании, но и в прогнозировании. Прогнозирование тесно связано с планированием и обычно предшествует ему. Методы корреляции используются для прогнозирования потребности в различных видах продукции, для прогноза параметров технических систем и других целей. Результаты корреляционно-регрессионного анализа могут быть использованы для планирования и прогнозирования уровня результативного показателя. Вопрос № 21. Особенности, значение и сущность выборочного наблюдения. Выборочное наблюдение – один из видов несплошного статистического наблюдения. Сущность выборочного наблюдения заключается в том, что исследуется только часть и результаты переносят на всю совокупность. Выборочное наблюдение находит широкое применение во всех отраслях хозяйственной деятельности. Выборки используются при опросах общественного мнения, покупательского спроса, формирования доходов и структуры расходов населения и т.д. Та совокупность, из которой производится отбор, называется генеральной совокупностью; отобранная совокупность является выборочной совокупностью. Виды выборочного обследования:
Из-за того, что обследуется не вся совокупность, а только какая-то её часть, возникают ошибки выборочного наблюдения – ошибки репрезентативности. Средняя величина ошибки для выборочной совокупности, отобранной в случайном порядке: m = / 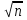 ,где m – средняя ошибка выборки; - среднее квадратическое отклонение; n – численность выборочной совокупности. Величина средней ошибки выборки зависит прежде всего от вариации значений признаков в выборочной совокупности (). Чем меньше среднее квадратическое отклонение, тем однороднее совокупность. Величина средней ошибки зависит и от численности выборки: чем больше единиц совокупности входит в выборку, тем меньше средняя ошибка выборки. При значении t=1 вероятность равна 0, 683; при t=2 вероятность равна 0, 954;при t=3 вероятность равна 0, 997.  Указывая вероятные пределы случайной ошибки выборки, мы тем самым указываем и те пределы, за которые не выйдет характеристика генеральной совокупности. Вопрос № 22. Современное состояние и задачи социально – экономической статистики в России. Социально – экономическая статистика использует научную методологию в конкретных условиях социальной и экономической деятельности общества. Она рассматривает производство, распределение и потребление материальных благ и услуг, закономерности их развития, экономические и социальные условия жизни людей, отображает качественные стороны общественных массовых явлений. Статистика в современных условиях обеспечивает госорганы информацией, необходимой для принятия решений, связанных с формированием экономической политики, разработкой различных государственных программ и мер по их реализации. При переходе к рыночной экономике произошли значительные изменения как в деятельности статистических органов, так и в построении статистических показателей. В новых условиях основное внимание сосредоточено на исчислении наиболее общих макроэкономических показателей, таких как ВВП, ВНП, потребление и накопление, сбережение, показатели занятости и инфляции, дефицита госбюджета, денежной массы, доходов населения и др. Политика в области статистики в настоящее время направлена на устранение недостатков и совершенствование методологии учёта и показателей в рамках международных стандартов и перехода к международной методологии, основанной на национальном счетоводстве (СНС). Система национальных счетов (СНС) – современная система информации для описания и анализа развития рыночной экономики, применяемая более чем в 150 странах мира с рыночной экономикой. На современном этапе в России статистические органы должны использовать новые современные технологии сбора, обработки, передачи и распространения статистической информации. Расширяется применение методов выборочного наблюдения при изучении деятельности разных хозяйственных субъектов и различных социальных процессов. Переход к международной методологии вносит изменения в представления о производственной экономической деятельности, пересматривается отношение к сфере услуг, уточняется классификация отраслей экономики по сферам деятельности, вводится новое деление экономики на секторы, вводятся новые понятия резидентов, трансфертов, экономической территории, и т.п. Вопрос № 23. Статистика населения. Для развития национальной экономики в целом и для развития ее основных отраслей необходима статистическая информация о населении. Как статистическая категория население представляет собой совокупность людей, проживающих на данной территории. Оно непрерывно изменяется за счет рождения и смертей. Основным источником информации о населении является текущий учет (сплошная перепись) населения, который, как правило, проводится раз в десять лет. Отдельные сведения собираются на основе выборочной переписи населения. При переписи населения учитываются две категории населения: наличное население (лица, фактически находящиеся на момент переписи в данном населенном пункте, включая временно проживающих) и постоянное население (лица, для которых данный населенный пункт является местом постоянного проживания, включая временно отсутствующих). В ходе статистического обследования населения определяется численность населения на момент проведения переписи. Сведения о наличном населении очень важны для населенных пунктов, где сильно влияние сезонного фактора (курортные районы) или для поселков, где используется рабочая сила вахтовым методом. По результатам переписи исчисляется такой показатель, как среднегодовая численность населения, которая представляет собой среднюю арифметическую из численности на начало и конец календарного периода. Показатель среднегодовой численности широко используется для расчетов среднедушевых показателей (потребления, доходов, обеспечения транспортными коммуникациями, товарами потребления, услугами и т.д.). Демографическая ситуация в стране характеризуется такими показателями: численность населения, рождаемость, смертность, естественный прирост, брачность, разводимость и т.д. Объектом статистического наблюдения могут быть самые разные совокупности населения (в целом по стране) и отдельные группы населения – экономически активные, безработные, пенсионеры, городское население или сельское, мужчины и женщины. При определении численности населения могут учитываться разные категории населения. Численность населения постоянно изменяется в течение года, поэтому целесообразно определять среднюю численность населения за период одним из следующих способов: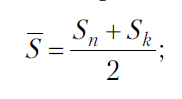 
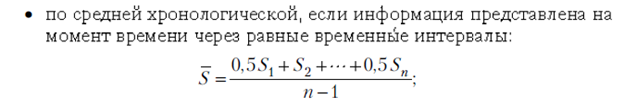 Население распределено неравномерно по отдельным регионам страны.  Для сравнения рассчитываются показатели:
Население как статистическая совокупность весьма неоднородно, поэтому возникает необходимость изучения населения по группам и подгруппам по следующим критериям: по полу, возрасту, семейному положению, национальности, по уровню образования, по источника средств существования и др. Численность населения изменяется за счёт рождений и смертей, что составляет так называемое естественное движение. Основными показателями, характеризующими естественное движение, являются: |
).
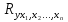