Вопросы к экзамену по мат. анализу_3 курс_5 семестр. Вопросы к экзамену (3 курс, 5 семестр)

• Название: Вопросы к экзамену (3 курс, 5 семестр)
• Дата: 18.01.2022
• Размер: 16.72 Kb.
• Имя файла: Вопросы к экзамену по мат. анализу_3 курс_5 семестр.docx
• Тип: Вопросы к экзамену; #334882

Вопросы к экзамену

(3 курс, 5 семестр)
1. Сформулируйте определения числового ряда и его суммы. Приведите примеры. Объясните связь числового ряда и числовых последовательностей. Опишите понятие остатка ряда.

2. Опишите понятия сходящегося и расходящегося рядов. Приведите примеры. Исследуйте сумму членов геометрической прогрессии. Сформулируйте свойства сходящихся рядов. Приведите примеры их применения.

3. Сформулируйте и докажите необходимое условие сходимости числового ряда. Приведите пример, иллюстрирующий необходимое условие сходимости ряда, и контрпример достаточности этого условия для сходимости ряда. Опишите гармонический ряд.

4. Сформулируйте критерий Коши сходимости числового ряда и критерий Коши расходимости ряда. Приведите пример применения этих критериев к доказательству сходимости и расходимости числовых рядов.

5. Опишите гармонический ряд и докажите его расходимость с помощью критерия Коши.

6. Опишите обобщенный гармонический ряд. Докажите сходимость этого ряда при 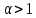, используя ограниченность его частичных сумм.

7. Опишите ряд с неотрицательными членами, приведите примеры. Сформулируйте и докажите необходимое и достаточное условие сходимости числового ряда с неотрицательными членами.

8. Сформулируйте признаки сравнения (простой и предельный) сходимости рядов с неотрицательными членами. Опишите схему их применения, приведите примеры. Объясните, что такое мажоранта и миноранта.

9. Сформулируйте предельный признак Даламбера сходимости рядов с неотрицательными членами. Объясните схему его применения к исследованию числовых рядов, приведите пример.

10. Сформулируйте предельный признак Коши сходимости рядов с неотрицательными членами. Объясните схему его применения к исследованию числовых рядов, приведите пример.

11. Сформулируйте интегральный признак сходимости рядов с неотрицательными членами. Объясните схему его применения к исследованию числовых рядов, приведите пример. Опишите «дзета-функцию Римана».

12. Опишите знакочередующийся ряд. Сформулируйте определения абсолютно сходящегося ряда и условно сходящегося ряда. Приведите примеры. Сформулируйте и докажите теорему о сходимости абсолютно сходящегося ряда.

13. Опишите понятие ряда Лейбница, приведите пример. Сформулируйте и докажите теорему о сходимости ряда Лейбница. Объясните схему применения признака Лейбница к исследованию числовых рядов.

14. Опишите процесс нахождения суммы знакочередующегося ряда с заданной точностью. Приведите пример.

15. Сформулируйте признаки Абеля и Дирихле сходимости числовых рядов. Объясните схему их применения к исследованию числовых рядов.

16. Сформулируйте свойства абсолютно сходящихся рядов и одно из них докажите. Сравните эти свойства со свойствами конечных сумм. Приведите примеры. Объясните правило умножения абсолютно сходящихся рядов.

17. Сформулируйте определение условно сходящегося ряда, приведите примеры. Сравните свойства условно сходящихся рядов со свойствами конечных сумм. Сформулируйте теорему Римана для условно сходящихся рядов.

18. Сформулируйте определения функциональной последовательности и функционального ряда. Приведите примеры. Опишите понятия суммы и остатка функционального ряда, сформулируйте определения функциональной последовательности, ограниченной на множестве, возрастающей (убывающей) на множестве. Приведите примеры.

19. Сформулируйте определения сходящихся в точке (на множестве) функциональной последовательности и функционального ряда. Опишите понятия абсолютно сходящегося функционального ряда и области сходимости функционального ряда. Приведите примеры.

20. Введите понятие степенного ряда, приведите примеры. Сформулируйте и докажите теорему Абеля о сходимости степенного ряда. Приведите его геометрическую интерпретацию. Какие три случая сходимости степенного ряда возможны?

21. Введите понятие радиуса сходимости степенного ряда по степеням 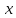. Сформулируйте теорему о радиусе сходимости степенного ряда. Объясните схему нахождения радиуса сходимости степенного ряда.

22. Объясните схему нахождения области сходимости степенного ряда. Какое множество точек может составлять область сходимости степенного ряда? Как соотносятся радиусы сходимости данного ряда, ряда, полученного из данного дифференцированием и ряда, полученного из данного интегрированием?

23. Сформулируйте и докажите теорему о единственности разложения функции в степенной ряд. Сформулируйте определение ряда Тейлора. Опишите ряд Маклорена.

24. Сформулируйте теорему, выражающую достаточный признак сходимости ряда Тейлора. Опишите разложение показательной функции 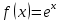в ряд Тейлора, проверьте выполнение достаточного условия разложимости этой функции в ряд Тейлора.

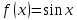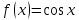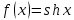25. Опишите разложение тригонометрических функций и в ряд Тейлора, проверьте выполнение достаточного условия разложимости этих функций в ряд Тейлора. Приведите разложение гиперболических функций и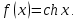

26. Сформулируйте определение ряда Тейлора. Опишите разложение логарифмической функции 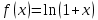в ряд Тейлора, укажите промежуток сходимости этого ряда.

27. Опишите разложение в ряд Тейлора степени бином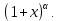а Укажите промежуток сходимости этого ряда. Приведите частные случаи разложения степени бинома в ряд Тейлора.

28. Опишите методы разложения функций в степенные ряды: дифференцирование, интегрирование, разложение на сумму простейших дробей, приведите примеры.

29. Опишите схему применения степенных рядов к приближенным вычислениям, приведите примеры.

30. Опишите понятия квадрируемой области, диаметра замкнутой области, интегральной суммы для функции двух переменных. Используя аналогию с определенным интегралом Римана, введите понятие двойного интеграла, уточните понятие предела интегральной суммы.

31. Опишите условия существования двойного интеграла: необходимые, достаточные. Изложите идею их доказательства.

32. Введите понятия нижней и верхней сумм Дарбу, опишите некоторые их свойства, сравните с интегральными суммами. Сформулируйте критерий интегрируемости функции двух переменных, изложите идею его доказательства.

33. Опишите процесс вычисления площади с помощью двойного интеграла и обоснуйте соответствующую формулу. Введите понятие элемента площади.

34. Сформулируйте задачу, решение которой приводит к геометрическому смыслу двойного интеграла. Опишите процесс её решения, используя аналогию с вычислением площади криволинейной трапеции в случае интеграла Римана.

35. Сформулируйте основные свойства двойного интеграла, докажите одно из них. Приведите примеры.

36. Сформулируйте и докажите теорему о среднем значении для двойного интеграла. Приведите его геометрическую интерпретацию.

37. Опишите процесс вычисления двойного интеграла сведением его к повторному в случае прямоугольной области интегрирования. Приведите пример.

38. Опишите процесс вычисления двойного интеграла сведением его к повторному в случае произвольной области интегрирования. Приведите пример.

39. Опишите процесс изменения порядка интегрирования при вычислении двойного интеграла сведением к повторному. Приведите примеры.

40. Запишите формулу замены переменных в двойном интеграле и формулу перехода в двойном интеграле к полярным координатам. Сформулируйте правило замены переменных в двойном интеграле. Приведите пример.

41. Опишите процесс вычисления площади с помощью двойного интеграла в декартовых и полярных координатах. Приведите примеры.

42. Опишите приложения двойного интеграла к вычислению площади фигуры и объема тела. Запишите соответствующие формулы.

43. Опишите приложения двойного интеграла к нахождению массы неоднородной пластины, статических моментов и координат центра тяжести плоской фигуры.

44. Опишите криволинейные интегралы 1-го рода и их геометрический смысл. Сформулируйте основные свойства этих интегралов.

45. Опишите процесс вычисления криволинейных интегралов 1-го рода. Приведите примеры.

46. Опишите криволинейные интегралы 2-го рода. Сформулируйте основные свойства этих интегралов. Приведите примеры.

47. Опишите процесс вычисления криволинейных интегралов 2-го рода. Приведите примеры.

48. Запишите формулу Грина-Остроградского, устанавливающую связь криволинейного интеграла 2-го рода общего вида с двойным интегралом. Приведите пример её применения к вычислению криволинейного интеграла.