Документ Microsoft Word (2). Введение 1 Цепные дроби 2 Подходящие дроби 3 Представление рациональных чисел цепными дробями 3 Разложение действительного иррационального числа в правильную бесконечную цепную дробь 4
 Скачать 0.52 Mb.
|
 . В самом деле:если n=1, то если n=2, то  ; поэтому  если n>2, то  = где >1, т.к.  Поэтому и здесь  . Докажем то, что рациональное число  однозначно представляется цепной дробью , если  .Пусть  с условием ,  . Тогда  , так что  . Повторным сравнением целых частей получаем  , а следовательно  и так далее. Если  , то в продолжении указанного процесса получим также  . Если же  , например  , то получим  , что невозможно.Теорема доказана. Вместе с тем мы установили, что при соблюдении условия между рациональными числами и конечными цепными дробями существует взаимно однозначное соответствие.Разложение действительного иррационального числа в правильную бесконечную цепную дробь Разложение действительного иррационального числа в правильную бесконечную цепную дробь. В предыдущей главе мы рассмотрели, как в процессе последовательного выделения целой части и перевертывания дробной рациональная дробь разлагается в конечную непрерывную дробь. =( )(1)и, наоборот, свертывание такой непрерывной дроби приводит к рациональной дроби. Процесс выделения целой части и перевертывания дробной можно применить к любому действительному числу. Для иррационального числа  указанный процесс должен быть бесконечным, так как конечная цепная дробь равна рациональному числу.Выражение (где  ,  ) (2)возникающее в таком процессе или заданное формально, мы будем называть правильной бесконечной цепной, или непрерывной дробью, или дробью бесконечной длины и обозначать кратко через (  ), а числа  – ее элементами или неполными частными.Отметим, что разложение возможно только в единственном виде, так как процесс выделения целой части – процесс однозначный.Рассмотрим пример разложения иррационального числа .Пусть  . Выделим из  его целую часть.  =3, а дробную часть –3, которая меньше 1, представим в виде  , где  .Повторяя операцию выделения целой части и перевертывания дробной, мы получаем:  ; ; .Если остановиться на этом шаге, то можно записать: 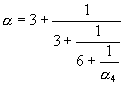 С другой стороны, из формулы для  видно, что =3+ . Поэтому  , вследствие чего, начиная с этого момента, неполные частные станут повторяться.Бесконечная непрерывная дробь, в которой определенная последовательность неполных частных, начиная с некоторого места, периодически повторяется, называется периодической непрерывной дробью. Если, в частности, периодическое повторение начинается с первого звена, то цепная дробь называется чисто периодической, в противном случае – смешанной периодической. Чисто периодическая дробь  записывается в виде  , а смешанная периодическая  в виде  .Итак, разлагается в смешанную периодическую дробь (3, 3, 6, 3, 6, …) или (3, (3, 6)).В общем случае разложения действительного иррационального числа 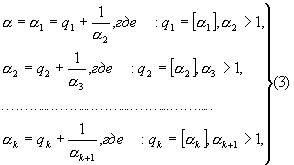поступаем так же, как в примере. Останавливаясь при этом в процессе выделения целой части после k–го шага, будем иметь: так что 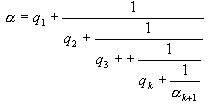 Числа  называются остаточными числами порядка k разложения . В формуле (4) имеем кусок разложения до остаточного числа  .Для бесконечной цепной дроби (2) можно построить бесконечную последовательность конечных непрерывных дробей.  Эти дроби называют подходящими дробями. Закон образования соответствующих им простых дробей будет такой же, как и для подходящих дробей в случае конечных непрерывных дробей, так как этот закон зависит только от неполных частных  и совершенно не зависит от того, является ли  последним элементом или за ним следует еще элемент  . Поэтому для них сохранятся также остальные свойства, которые выводятся из закона образования числителей и знаменателей подходящих дробей.В частности, мы имеем:  , причем  ; , откуда следует несократимость подходящих дробей  ; .Сравним теперь подходящую дробь  и кусок разложения до остаточного числа . Имеемоткуда видно, что вычисление по  формально производится таким же образом, как вычисление по с тем лишь отличием, что в первом случае заменяется на  , а во втором заменяется на  . Поэтому на основании формулы  можно сделать вывод о справедливости следующего важного соотношения . (5)По этой причине мы пишем также  , хотя не является здесь целым положительным числом.При помощи формулы (5) можно вывести следующую теорему и расположении подходящих дробей разложения  .Теорема: Действительное число всегда находится между двумя соседними подходящими дробями своего разложения, причем оно ближе к последующей, чем к предыдущей подходящей дроби.Доказательство: Из формулы (5) следует  Но  ,  , так что  (  ) и ( ) имеют одинаковый знак, а это значит, что находится между  и ; , то есть ближе к , чем к .Теорема доказана. Так как  , то  , и так далее; отсюда приходим к следующему заключению о взаимном расположении подходящих дробей: больше всех подходящих дробей нечетного порядка и меньше всех подходящих дробей четного порядка;подходящие дроби нечетного порядка образуют возрастающую последовательность, а четного порядка – убывающую (в случае иррационального  |