 указанные последовательности являются бесконечными), то есть указанные последовательности являются бесконечными), то есть

(в случае рационального   ). ).
Учитывая то, что при   , вследствие чего , вследствие чего 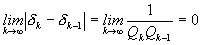 , переходим к дальнейшему выводу, что в случае иррационального , переходим к дальнейшему выводу, что в случае иррационального  сегменты сегменты  , , 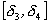 , … образуют стягивающуюся последовательность, которая, как известно, должна иметь единственную общую точку, являющуюся общим пределом последовательностей , … образуют стягивающуюся последовательность, которая, как известно, должна иметь единственную общую точку, являющуюся общим пределом последовательностей  , ,  , … и , … и 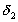 , , 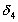 , … . Но так как , … . Но так как  принадлежит всем сегментам последовательности, то принадлежит всем сегментам последовательности, то  и совпадает с указанной точкой, так что и совпадает с указанной точкой, так что  . .
Итак, мы имеем следующий важный результат:
бесконечная последовательность подходящих дробей 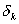 , которая возникает при разложении иррационального , которая возникает при разложении иррационального  , сходится к , сходится к  , колеблясь около него. Или: иррациональное действительное , колеблясь около него. Или: иррациональное действительное  равно пределу последовательности подходящих дробей своего разложения в бесконечную непрерывную дробь (процессом выделения целой части). равно пределу последовательности подходящих дробей своего разложения в бесконечную непрерывную дробь (процессом выделения целой части).
Цепные дроби как вычислительный инструмент
Целое число, являющееся делителем каждого из целых чисел  , называется общим делителем этих чисел. Общий делитель этих чисел называется их наибольшим общим делителем, если он делится на всякий общий делитель данных чисел. , называется общим делителем этих чисел. Общий делитель этих чисел называется их наибольшим общим делителем, если он делится на всякий общий делитель данных чисел.
Пусть - рациональное число, причем b>0. Применяя к a и b алгоритм Евклида для определения их наибольшего общего делителя, получаем конечную систему равенств:
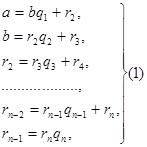
Где неполным частным последовательных делений 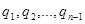 соответствуют остатки соответствуют остатки  с условием b> > >…> >0, а соответствует остаток 0. с условием b> > >…> >0, а соответствует остаток 0.
Системе равенств (1) соответствует равносильная система
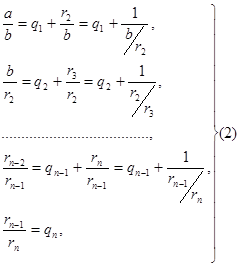
Из которой последовательной заменой каждой из дробей  и т. д. ее соответствующим выражением из следующей строки получается представление дроби в виде: и т. д. ее соответствующим выражением из следующей строки получается представление дроби в виде:


Такое выражение называется правильной (конечной) цепной или правильной непрерывной дробью, при этом предполагается, что – целое число, а , …, - натуральные числа.
Имеются различные формы записи цепных дробей:


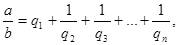

Согласно последнему обозначению имеем

Числа , , …, называются элементами цепной дроби.
Алгоритм Евклида дает возможность найти представление (или разложение) любого рационального числа в виде цепной дроби. В качестве элементов цепной дроби получаются неполные частные последовательных делений в системе равенств (1), поэтому элементы цепной дроби называются также неполными частными. Кроме того, равенства системы (2) показывают, что процесс разложения в цепную дробь состоит в последовательном выделении целой части и перевертывании дробной части.
Последняя точка зрения является более общей по сравнению с первой, так как она применима к разложению в непрерывную дробь не только рационального, но и любого действительного числа.
Разложение рационального числа имеет, очевидно, конечное число элементов, так как алгоритм Евклида последовательного деления a на b является конечным.
Понятно, что каждая цепная дробь представляет определенное рациональное число, то есть равна определенному рациональному числу. Но возникает вопрос, не имеются ли различные представления одного и того же рационального числа цепной дробью? Оказывается, что не имеются, если потребовать, чтобы было .
Теорема. Существует одна и только одна конечная цепная дробь, равная данному рациональному числу, но при условии, что .
Д о к а з а т е л ь с т в о: 1) Заметим, что при отказе от указанного условия единственность представления отпадает. В самом деле, при :

Так что представление можно удлинить:
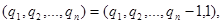
Например, (2, 3, 1, 4, 2)=( 2, 3, 1, 4, 1, 1).
2) Принимая условие , можно утверждать, что целая часть цепной дроби 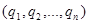 равна ее первому неполному частному . В самом деле: равна ее первому неполному частному . В самом деле:
1. если n=1, то
2. если n=2, то 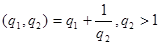 ; поэтому ; поэтому 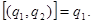
3. если n>2, то
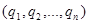 = =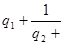
,
Где 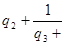 >1, т. к. >1, т. к.
Поэтому и здесь 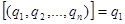 . Докажем то, что рациональное число однозначно представляется цепной дробью . Докажем то, что рациональное число однозначно представляется цепной дробью 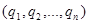 , если . , если .
Пусть 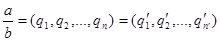 с условием , . Тогда с условием , . Тогда 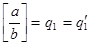 , так что , так что  . Повторным сравнением целых частей получаем , а следовательно . Повторным сравнением целых частей получаем , а следовательно 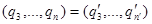 и так далее. Если , то в продолжении указанного процесса получим также . Если же , например , то получим и так далее. Если , то в продолжении указанного процесса получим также . Если же , например , то получим 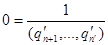 , что невозможно. , что невозможно.
Теорема доказана.
Вместе с тем мы установили, что при соблюдении условия между рациональными числами и конечными цепными дробями существует взаимно однозначное соответствие.
З а м е ч а н и я
1. В случае разложения правильной положительной дроби первый элемент , например, 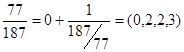 . .
2. При разложении отрицательной дроби (отрицательный знак дроби всегда относится к числителю) первый элемент будет отрицательным, остальные положительными, так как целая часть отрицательной дроби является целым отрицательным числом, а ее дробная часть, как всегда, положительна.
Пример: 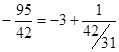 , а так как , а так как  , то , то 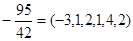 . .
3. Всякое целое число можно рассматривать как непрерывную дробь, состоящую из одного элемента.
Пример: 5=(5); 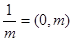 . .
6.Использование цепных дробей при решении диофантовых уравнений
Можно найти НОД натуральных чисел a и b, не раскладывая эти числа на простые множители, а применяя процесс деления с остатком. Для этого надо разделить большее из этих чисел на меньшее, потом меньшее из чисел на остаток при первом делении, затем остаток при первом делении на остаток при втором делении и вести этот процесс до тех пор, пока не произойдет деление без остатка. Последний отличный от нуля остаток и есть искомый НОД (a, b). Чтобы доказать это утверждение, представим описанный процесс в виде следующей цепочки равенств: если a>b, то
a = bq0 + r1
b = r1q1 + r2
r1 = r2q2 + r3 (1)
. . . . . . . . . . . .
rn – 1 = rnqn
Затем r1, . . . , rn - положительные остатки, убывающие с возрастанием номера. Из первого равенства следует, что общий делитель чисел a и b делит r1 и общий делитель b и r1 делит a, поэтому НОД (a,b) = НОД (b, r1) = НОД (r1, r2) = … = НОД (rn -1, rn)= = НОД (rn, 0) = rn.
Утверждение доказано. Приведённый способ нахождения НОД носит название метода последовательного деления с остатком или алгоритма Евклида, поскольку впервые он был изложен в его «Началах».
Обратимся к системе (1). Из первого равенства, выразив остаток r1 через a и b, получим r1 = a – bq0. Продолжая этот процесс, мы можем выразить все остатки через a и b, получим r1 = a – bq0. Подставляя его во второе равенство, найдём r2 = b(1 + q0q1) – aq1. Продолжая этот процесс дальше, мы сможем выразить все остатки через a и b, в том числе и последний: rn = Aa + Bb. В результате нами доказано предложение: если d – наибольший общий делитель натуральных чисел a и b, то найдутся такие целые числа A и B, что d = Aa + Bb. Заметим, что коэффициенты A и B имеют разные знаки; если НОД (a,b) = 1, то Aa + Bb = 1. Как найти числа A и B, видно из алгоритма Евклида.
Перейдем теперь к решению линейного уравнения с двумя неизвестными. Оно имеет вид: ax + by = c Возможны два случая: либо число c делится на d = НОД(a,b), либо нет. В первом случае можно разделить обе части уравнения на d и свести задачу к решению в целых числах уравнения a1x = b1y = c1, коэффициенты которого a1 = a/d и b1 = b/d взаимно просты. Во втором случае уравнение не имеет целочисленных решений: при любых целых x и y число
ax + by делиться на d и поэтому не может равняться числу c, которое на d не делится.
Итак, мы можем ограничиться случаем, когда в уравнении (2) коэффициенты a и b взаимно просты. На основании предыдущего предложения найдутся такие целые числа х0 и у0, что ax0 + by0 = 1, откуда пара (сх0, су0) удовлетворяет уравнению (2). Вместе с ней уравнению (2) удовлетворяет бесконечное множество пар (х, у) целых чисел, которые можно найти по формулам
х = сх0 + bt, y = cy0 – at. (3)
Здесь t – любое число. Нетрудно показать, что других целочисленных решений уравнение ах + by = c не имеет. Решение, записанное в виде (3), называется общим решением уравнения (2). Подставив вместо t конкретное целое число, получим его частное решение.
Задача 2.
Найдём, например, целочисленные решения уравнения 2x + 5y = 17. Решение.
Применив к числам 2 и 5 алгоритм Евклида, получим 2 * 3 – 5 = 1. Значит, пара сх0 = 3 * 17, су0 = - 1 * 17 удовлетворяет уравнению 2х + 5у = 17. Поэтому общее решение исходного уравнения таково:
x = 51 + 5t, у = - 17 – 2t, где t принимает любые целые значения. Очевидно, неотрицательные решения отвечают тем t, для которых выполняются неравенства
⎧ 51 + 5t ≥ 0
⎨
⎩ - 17 - 2t ≥ 0
Отсюда найдём – 51/5 ≤ t ≤ - 17/2. Этим неравенством удовлетворяют числа - 10, - 9. Соответствующие частные решения запишутся в виде пар: (1,3), (6, 1).
Задача 4.
Крестьянка несла на базар корзину яиц. Неосторожный всадник, обгоняя женщину, задел корзину, и все яйца разбились. Желая возместить ущерб, он спросил у крестьянки, сколько яиц было в корзине. Она ответила, что число яиц не знает, но когда она раскладывала их по 2, по 3, по 4, по 5 и по 6, то каждый раз одно яйцо оставалось лишним, а когда она разложила по 7, лишних яиц не осталось. Сколько яиц несла крестьянка на базар?
Решение.
Пусть х – число яиц. Так как х – 1 делится на 2, на 3, на 4, на 5, на 6, то оно делится на их НОК, равное 60. Значит, х имеет вид 60у + 1. Поэтому для ответа на вопрос задачи надо решить в натуральных числах уравнение 60у + 1 = 7z. С помощью алгоритма Евклида находим у0 = -2, z0 = - 17, откуда все целочисленные решения уравнения имеют вид у = -2 + 7t, z = -17 + 60t, где t – любое целое число. Наименьшее положительное решение получаем при t = 1. В этом случае у = 5, z = 43. Итак, крестьянка несла на базар 301 яйцо.
Ответ. Крестьянка несла на базар 301 яйцо. [2, с. 75 – 78]
Следующий метод связан с непрерывными или цепными дробями.
Обратимся вновь к алгоритму Евклида. Из первого равенства системы (1) вытекает, что дробь a/b можно записать в виде суммы целой части и правильной дроби: a/b = q0 + r1/b. Но r1/b = 1/b/r1, и на основании второго равенства той же системы имеем b/r1 = q1 + r2/r1. Значит, a/b=q0+1/(q1+r2/r1). Далее получим a/b=q0 + 1/(q1+1/(q2+r3/r2)). Продолжим этот процесс до тех пор. Пока не придём к знаменателю qn.
В результате мы представим обыкновенную дробь a/b в следующем виде: a / b = q0 + 1 / (q1 + 1 / (…+ 1 / qn)). Эйлер назвал дроби такого вида непрерывными. Приблизительно в тоже время в Германии появился другой термин – цепная дробь. Так за этими дробями и сохранились оба названия. Ввиду громоздкости развёрнутой записи цепной дроби применяют компактную запись [q0; q1, q2, …,qn].
Задача 5.
Представить дробь 40/31 в виде цепной.
Решение.
40/31 = 1 + 9/31 = 1 + 1/3 /9 = 1 + 1/(3 + 4 / 9) = 1 + 1 / (3 + 1 / 9 / 4) = =1 + 1 / (3 + 1 / (2 +1 / 4)) = [1; 3, 2, 4]
Удобство применения цепных дробей заключается в том, что их свойства не связаны ни с какой системой счисления. По этой причине они эффективно используются в теоретических исследованиях. Но широкого практического применения цепные дроби не получили, так как для них нет удобных правил выполнения арифметических действий. [2, c. 79 – 81]
Заключение
Данная курсовая работа показывает значение цепных дробей в математике.
Бесконечные цепные дроби могут быть использованы для решения алгебраических и трансцендентных уравнений, для быстрого вычисления значений отдельных функций.
В настоящее время цепные дроби находят все большее применение в вычислительной технике, ибо позволяют строить эффективные алгоритмы для решения ряда задач на ЭВМ.
Список использованной литературы
1. М. О. Авдеева. Распределение неполных частных в конечных цепных дробях. — Владивосток : ИПМ ДВО РАН, 2000, с. 19.
2. М.О.Авдеева, В., А. Быковский. Решение задачи Арнольда о статистиках Гаусса-Кузьмина. — Препринт ДВО РАН №08, Дальнаука, Владивосток, 2002.
3. М. О. Авдеева. О статистиках неполных частных конечных цепных дробей. — Функц. анализ и его прил. т. 38, Я2 2, 2004, с. 1-11.
4. В. А. Быковский. Оценка дисперсии длин конечных непрерывных дробей. ФПМ, t. И, №6, 2005, с. 15-26.
5. Галочкин А. П., Нестереико Ю. В., Шидловский А. Б. Введение в теорию чисел. — М.: Изд-во Моск. ун-та, 1984.
6. А. А. Карацуба. Основы аналитической теории чисел. — М., Наука, 1983.
7. Р. О. Кузьмин. Об одной задаче Гаусса. ДАН ССР, 1928, с. 375-380.
8. Р. О. Кузьмин. К метрической теории непрерывных дробей. — Ученые записки ЛГУ, сер. матем. наук, вып. 15, 1948, с. 163-173.111
9. В.Н.Попов. Асимптотика суммы сумм элементов непрерывных дробей чисел вида а/р. — Аналитическая теория чисел и теория функций. 2, Зап. научн. сем. ЛОМИ, 91, Изд-во «Наука», Ленинград, отд., Л., 1979, с. 81-93
10. А.В.Устинов. Асимптотическое поведение первого и второго м.оментов для числа шагов в алгоритме Евклида. — Известия РАН, т. 72, №5, 2008, с. 86-216.
11. А.В.Устинов. О среднем числе шагов в алгоритме Евклида с выбором минимального по модулю остатка. — Матем. заметки, т. 85, №1, 2009, с. 153-156.
12. А. В. Устинов. О статистических свойствах конечных цепных дробей. — Труды по теории чисел, Зап. научн. сем. ПОМИ, 322, ПОМИ, СПб., 2005, с. 186-211.
13. А. В. Устинов. О статистиках Гаусса-Кузьмина для конечных цепных дробей. — Фунд. и прикл. математика, т. 11, 2005, с. 195-208.
14. А.В.Устинов. Вычисление дисперсии в одной задаче из теории цепных дробей. — Мат. сборник, т. 198, № 6, 2007, с. 139-158.
15. Ю. Ю. Финкелынтейн. Полигоны Клейна и приведенные регулярные непрерывные дроби. — Успехи мат. наук, 1993, т. 48, Вып. 3, с. 205-206.
16. А. Я. Хинчин. Избранные труды по теории чисел. — М., МЦНМО, 2006.
17. А. Я. Хинчин. Цепные дроби. — М., Наука, 1978.112
18. A. H. Xhhhhh. Metrische Kettenbruechproblem. — Compos. Math. 1935, Bd. 1, pp. 361-382
19. A. R. Xhhhhh. Zur metrischen Kettenbruechtheorie. — Compos. Math. 1936, Bd.3, №2, pp. 276-285
20. J.C.Alexander, D. B.Zagier. The entropy of certain infitely convolved Bernoulli measures. — J. London Math. Soc., v. 44, 1991, pp. 121-134.
21. A. Denjoy. Sur une fonction reele de Minkowski. — J. Math. Pures Appl. v. 17, 1938, pp. 105-151.
22. J. D. Dixon. The number of steps in the Euclidean algorithm. — J. Number Theory, v. 2, 1970, pp. 414-422.
23. D. Hensley. The Number of Steps in the Euclidean Algorithm. — J. of Number Theory, v. 49, 1994, pp. 142-182.
24. S. R. Finch. Mathematical constants.
Encyclopedia Math. Appl., 94, Cambridge Univ. Press, Cambridge, 2003.
25. J. P. Graber, P. Kirschenhofer, R. F. Tichy. Combinatorial and arithmetical properties of linear numeration systems. — Combinatorica v. 22, №2, 2002, pp. 245-267.
26. G.H.Hardy, E.M.Wright. An Introduction to the Theory of Numbers. — Oxford University Press, Oxford, 1980.
27. H. Heilbronn. On the average length of a class of finite continued fractions. — in Abhandlungen aus Zahlentheorie und Analysis, Berlin, VEB, 1968, pp. 89-96.
28. B.Vallee. A unifying framework for the analysis of a class of Euclidean algorithms. — Proceedings of LATIN'2000, Lecture Notes in Computer Science 1776, Springer, pp. 343-354.
29. B. Vallee. Dynamical analysis of a class of Euclidean algorithms. — Theoretical computer science, v. 297, 2003, pp. 447-486.
30. B.Vallee, V. Baladi. Euclidean algorithms are gaussian. — J. Number Theory, v. 110, 2005, pp. 331-386. |
 Скачать 0.52 Mb.
Скачать 0.52 Mb.
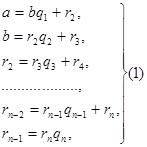
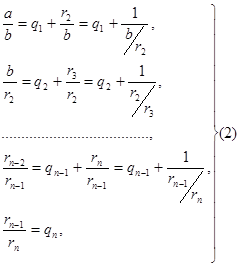



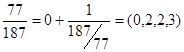 .
.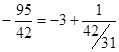 , а так как
, а так как